浙教版七上图形初步认识压轴题动点专项训练(含解析)
文档属性
| 名称 | 浙教版七上图形初步认识压轴题动点专项训练(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-19 17:36:52 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
图形初步认识压轴题专项训练
1.已知:直线AB与直线CD交于点O,过点O作OE⊥AB.
(1)如图1,OP为∠AOD内的一条射线,若∠1=∠2,求证:OP⊥CD;
(2)如图2,若∠BOC=2∠AOC,求∠COE的度数;
(3)如图3.在(2)的条件下,过点O作OF⊥CD,经过点O画直线MN,若射线OM平分∠BOD,请直接写出图中与2∠EOF度数相等的角.
2.如图①,已知OC是∠AOB内部的一条射线,M、N分别为OA、OB上的点,线段OM、ON同时开始旋转,线段OM以30度/秒绕点O逆时针旋转,线段ON以10度/秒的速度绕点O顺时针旋转,当OM旋转到与OB重合时,线段OM、ON都停止旋转.设OM的旋转时间为t秒.
(1)若∠AOB=140°,当t=2秒时,∠MON=________,当t=4秒时,∠MON=________;
(2)如图②,若∠AOB=140°,OC是∠AOB的平分线,求t为何值时,两个角∠NOB与∠COM中的其中一个角是另一个角的2倍.
(3)如图③,若OM、ON分别在∠AOC、∠COB内部旋转时,总有∠COM=3∠CON,请直接写出
的值.
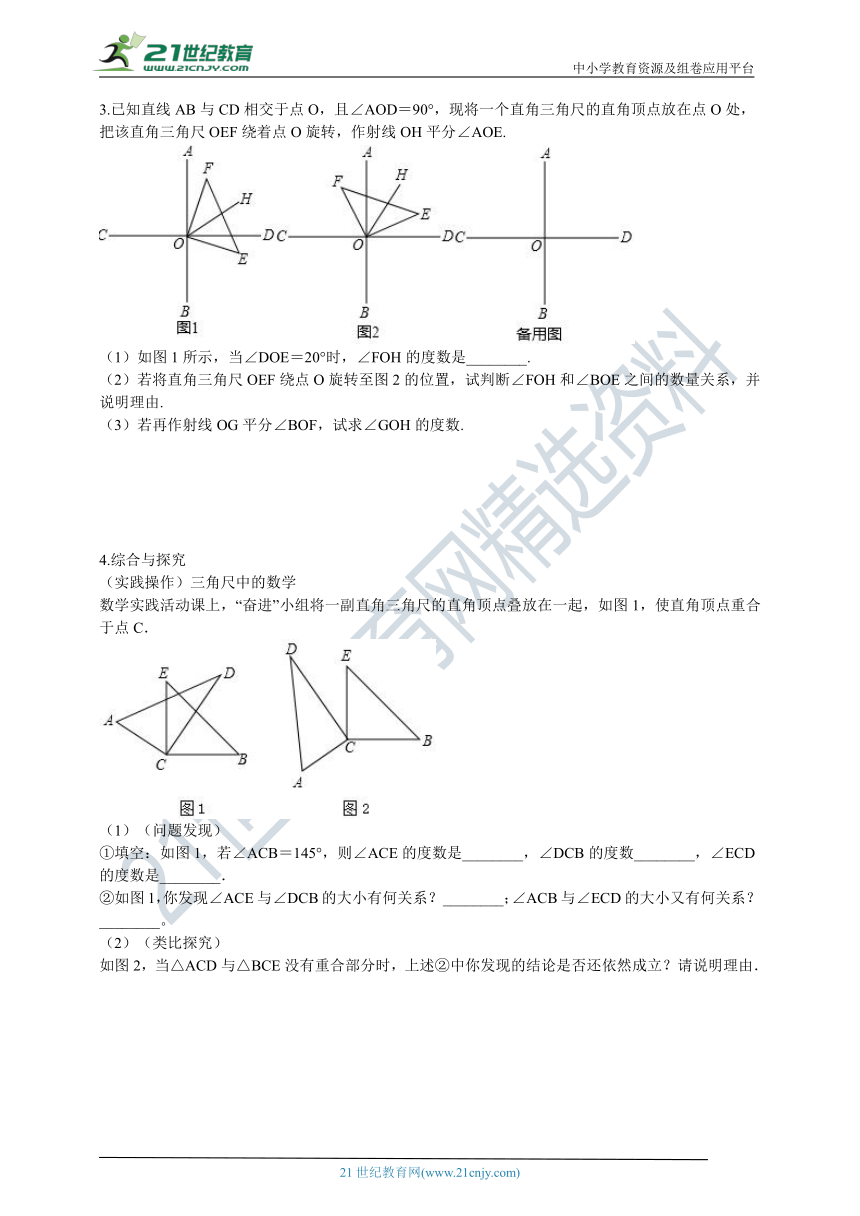
3.已知直线AB与CD相交于点O,且∠AOD=90°,现将一个直角三角尺的直角顶点放在点O处,把该直角三角尺OEF绕着点O旋转,作射线OH平分∠AOE.
(1)如图1所示,当∠DOE=20°时,∠FOH的度数是________.
(2)若将直角三角尺OEF绕点O旋转至图2的位置,试判断∠FOH和∠BOE之间的数量关系,并说明理由.
(3)若再作射线OG平分∠BOF,试求∠GOH的度数.
4.综合与探究
(实践操作)三角尺中的数学
数学实践活动课上,“奋进”小组将一副直角三角尺的直角顶点叠放在一起,如图1,使直角顶点重合于点C.
(1)(问题发现)
①填空:如图1,若∠ACB=145°,则∠ACE的度数是________,∠DCB的度数________,∠ECD的度数是________.
②如图1,你发现∠ACE与∠DCB的大小有何关系?________;∠ACB与∠ECD的大小又有何关系?________。
(2)(类比探究)
如图2,当△ACD与△BCE没有重合部分时,上述②中你发现的结论是否还依然成立?请说明理由.
5.定义:若
,且
,则我们称
是
的差余角.例如:若
,则
的差余角
.
(1)如图1,点O在直线
上,射线
是
的角平分线,若
是
的差余角,求
的度数.
(2)如图2,点O在直线
上,若
是
的差余角,那么
与
有什么数量关系.
(3)如图3,点O在直线
上,若
是
的差余角,且
与
在直线
的同侧,请你探究
是否为定值?若是,请求出定值;若不是,请说明理由.
6.如图,已知
和
都是直角,它们有公共顶点O.
(1)若
,求
的度数.
(2)判断
和
的大小关系,并说明理由.
(3)猜想:
和
有怎样的数量关系,并说明理由.
7.已知,直线AB与直线CD相交于O,OB平分∠DOF.
(1)如图,若∠BOF=40°,求∠AOC的度数;
(2)作射线OE,使得∠COE=60°,若∠BOF=x°(
),求∠AOE的度数(用含x的代数式表示).
8.(1)如图1,点
在线段
上,
,
,点
,
分别是线段
,
的中点.求线段
的长;
(2)点
在线段
上,若
,点
,
分别是线段
,
的中点.你能得出
的长度吗?并说明理由.
(3)类似的,如图2,
是直角,射线
在
外部,且
是锐角,
是
的平分线,
是
的平分线.当
的大小发生改变时,
的大小也会发生改变吗?为什么?
9.点A
,
B在数轴上表示的数如图所示.动点P从点A出发,沿数轴向右以每秒2个单位长度的速度运动到点B
,
再从点B以同样的速度运动到点A停止,设点P运动的时间为t秒,解答下列问题.
(1)当t=2时,AP=个单位长度,当t=6时,AP=个单位长度;
(2)直接写出整个运动过程中AP的长度(用含t的代数式表示);
(3)当AP=6个单位长度时,求t的值;
(4)当点P运动到线段AB的3等分点时,t的值为.
10.如图(a),将两块直角三角尺的直角顶点C叠放在一起.
(1)若∠DCE=35°,∠ACB=________;若∠ACB=140°,则∠DCE=________;并猜想∠ACB与∠DCE的大小有何特殊关系,并说明理由________;
(2)如图(b),若是两个同样的三角尺60°锐角的顶点A重合在一起,则∠DAB与∠CAE的大小有何关系,请说明理由;
(3)已知∠AOB=α,∠COD=β(都是锐角),如图(c),若把它们的顶点O重合在一起,请直接写出∠AOD与∠BOC的大小相等的关系(用含有α,β的式子表示).
11.如图①,已知线段AB=12cm,点C为线段AB上的一个动点,点D、E分别是AC和BC的中点.
(1)若点C恰好是AB的中点,则DE=________cm;若AC=4cm,则DE=________cm;
(2)随着C点位置的改变,DE的长是否会改变?如果改变,请说明原因;如果不变,请求出DE的长;
(3)知识迁移:如图②,已知∠AOB=120°,过角的内部任意一点C画射线OC,若O
D、OE分别平分∠AOC和∠BOC,试说明∠DOE的度数与射线OC的位置无关.
12.如图1,已知数轴上有三点A、B、C,它们对应的数分别为a、b、c,且c-b=b-a;点C对应的数是10.
(1)若BC=15,
求a、b的值;
(2)如图2,在(1)的条件下,O为原点,动点P、Q分别从A、C同时出发,点P向左运动,运动速度为2个单位长度/秒,点Q向右运动,运动速度为1个单位长度/秒,N为OP的中点,M为BQ的中点.
①用含t代数式表示PQ、
MN;
②在P、Q的运动过程中,PQ与MN存在一个确定的等量关系,请指出他们之间的关系,并说明理由.
13.如图1,已知点C在线段AB上,线段AC=10厘米,BC=6厘米,点M,N分别是AC,BC的中点.
(1)求线段MN的长度;
(2)根据第(1)题的计算过程和结果,设AC+BC=a,其他条件不变,求MN的长度;
(3)动点P、Q分别从A、B同时出发,点P以2cm/s的速度沿AB向右运动,终点为B,点Q以1cm/s的速度沿AB向左运动,终点为A,当一个点到达终点,另一个点也随之停止运动,求运动多少秒时,C、P、Q三点有一点恰好是以另两点为端点的线段的中点?
14.如图(1),将两块直角三角尺的直角顶点C叠放在一起,
(1)若∠DCE=25°,∠ACB=?;若∠ACB=150°,则∠DCE=?;
(2)猜想∠ACB与∠DCE的大小有何特殊关系,并说明理由;
(3)如图(2),若是两个同样的直角三角尺60°锐角的顶点A重合在一起,则∠DAB与∠CAE的大小又有何关系,请说明理由.
15.如图(1),将两块直角三角板的直角顶点C叠放在一起.
(1)试判断∠ACE与∠BCD的大小关系,并说明理由;
(2)若∠DCE=30°,求∠ACB的度数;
(3)猜想∠ACB与∠DCE的数量关系,并说明理由;
(4)若改变其中一个三角板的位置,如图(2),则第(3)小题的结论还成立吗?(不需说明理由)
16.我们知道两直线交于一点,对顶角有2对,三条直线交于一点,对顶角有6对,四条直线交于一点,对顶角有12对,…
(1)10条直线交于一点,对顶角有多少对?
(2)n(n≥2)条直线交于一点,对顶角有多少对?
17.如图,直线AB与CD相交于点O,OP是∠BOC的平分线,OE⊥AB,OF⊥CD,
(1)图中除直角外,还有相等的角吗?请写出两对:①________;②________
.
(2)如果∠AOD=40°,则①∠BOC=________;②OP是∠BOC的平分线,所以∠COP=________度;③求∠BOF的度数________?.
18.如图,已知数轴上点A表示的数为8,B是数轴上一点,且AB=14.动点P从点A出发,以每秒5个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒.
(1)写出数轴上点B表示的数________
,
点P表示的数________(用含t的代数式表示);
(2)动点Q从点B出发,以每秒3个单位长度的速度沿数轴向左匀速运动,若点P、Q同时出发,问点P运动多少秒时追上点Q?
(3)若M为AP的中点,N为PB的中点.点P在运动的过程中,线段MN的长度是否发生变化?若变化,请说明理由;若不变,请你画出图形,并求出线段MN的长;
(4)若点D是数轴上一点,点D表示的数是x,请你探索式子|x+6|+|x﹣8|是否有最小值?如果有,直接写出最小值;如果没有,说明理由.
19.点
O
是直线
AB上一点,∠COD
是直角,OE平分∠BOC.
(1)①如图1,若∠DOE=25°,求∠AOC
的度数;
②如图2,若∠DOE=α,直接写出∠AOC的度数(用含α的式子表示);
(2)将图
1中的∠COD
绕点O按顺时针方向旋转至图
2
所示位置.探究∠DOE
与∠AOC
的度数之间的关系,写出你的结论,并说明理由.
20.如图1,已知∠MON=140°,∠AOC与∠BOC互余,OC平分∠MOB,
(1)在图1中,若∠AOC=40°,则∠BOC=°,∠NOB=°.
(2)在图1中,设∠AOC=α,∠NOB=β,请探究α与β之间的数量关系(必须写出推理的主要过程,但每一步后面不必写出理由);
(3)在已知条件不变的前提下,当∠AOB绕着点O顺时针转动到如图2的位置,此时α与β之间的数量关系是否还成立?若成立,请说明理由;若不成立,请直接写出此时α与β之间的数量关系.
答案解析部分
一、综合题
1.【答案】
(1)解:∵OE⊥AB
∴∠AOC+∠1=
∵∠1=∠2
∴∠AOC+∠2=
∴OP⊥CD
(2)解:∵∠AOC+∠BOC=
,且∠BOC=2∠AOC
∴∠AOC=
∵OE⊥AB
∴∠AOE=
∴∠COE=
-
=
(3)∠AOD、∠BOC、∠FON、∠EOM
2.【答案】
(1)60°;20°
(2)解:若∠COM=2∠BON时,|30°t﹣70°|=2×10°×t,
∴t=
或7(不合题意舍去)
当∠BON=2∠COM时,2|30°t﹣70°|=10°×t,
∴t=2或
,
综上所述当t=
或2或
时,两个角∠NOB与∠COM中的其中一个角是另一个角的2倍.
(3)解:∵∠COM=3∠CON,
∴∠AOB﹣∠BOC﹣30°×t=3(∠BOC﹣10°×t),
∴∠AOB=4∠BOC,
∴
=
.
3.【答案】
(1)35°
(2)解:∠BOE=2∠FOH,理由如下:
设∠AOH=x,
因为OH平分∠AOE
所以∠HOE=∠AOH=x
所以∠FOH=90
°﹣∠HOE=90°﹣x
∠BOE=180°﹣∠AOE=180°﹣2x
所以∠BOE=2∠FOH;
(3)解:如图3,当OE落在∠BOD内时,OF落在∠AOD内
因为OH平分∠AOE
所以∠HOE=∠AOH=
AOE
因为OG平分∠BOF
∠FOG=∠GOB=
BOF
所以∠GOH=∠GOF﹣∠FOH
=
BOF﹣(∠AOH﹣∠AOF)
=
(180°﹣∠AOF)﹣
AOE+∠AOF
=90°﹣
AOF﹣
(90°+∠AOF)+∠AOF
=90°﹣
AOF﹣45°﹣
AOF+∠AOF
=45°;
所以∠GOH的度数为45°;
如图4,当OE落在其他位置时
因为OH平分∠AOE
所以∠HOE=∠AOH=
AOE
因为OG平分∠BOF
∠FOG=∠GOB=
BOF
所以∠GOH=∠GOF+∠FOH
=
BOF+∠AOH+∠AOF
=
(180°﹣∠AOF)+
AOE+∠AOF
=90°﹣
AOF+
(90°﹣∠AOF)+∠AOF
=90°﹣
AOF+45°﹣
AOF+∠AOF
=135°;
所以∠GOH的度数为135°
综上所述:∠GOH的度数为45°
或135°.
4.【答案】
(1)5°;55°;35°;∠ACE=∠DCB;∠ACB+∠ECD=180°;
(2)解:结论:当
与
没有重合部分时,上述②中发现的结论依然成立.
理由:∵
,
∴
,
∴
,
∵
,
∴
,
∵
,
∴
,
∴
,
.
∴上述②中发现的结论依然成立.
5.【答案】
(1)解:如图,∵
是
的差余角
∴
-
=90°,
即
=
+90°,
又∵
是
的角平分线,
∴∠BOE=
,
则
+90°+
+
=180°,
解得
=30°;
(2)解:∵
是
的差余角,
∴
-
=90°,
∵
=
+
,
=
+
,
∴
-
=90°,
∵
=180°-
,
∴180°-
-
=90°,
∴
+
=90°;
(3)解:当OE在OC左侧时,
∵
是
的差余角,
∴
-
=90°,
∴∠AOE=∠BOE=90°,
则
=
=
=2;
当OE在OC右侧时,
过点O作OF⊥AB,
∵
是
的差余角,
∴
=90°+
,
又∵
=90°+
,
∴
=
,
∴
=
=
=
=
=2.
综上:
为定值2.
6.【答案】
(1)解:∵∠AOE=∠AOD-∠DOE=90°-60°=30°,
∴∠AOB=∠AOE+∠BOE=30°+90°=120°;
(2)解:相等,理由如下:
∵∠AOE=∠AOD-∠DOE=90°-∠DOE,
∠BOD=∠BOE-∠DOE=90°-∠DOE,
∴∠AOE=∠BOD
;
(3)解:∠AOB+∠DOE=180°,理由如下:
∵
∠AOB=∠AOE+∠BOE
=∠AOD-∠DOE+∠BOE
=90°+90°-∠DOE
=180°-∠DOE
,
∴∠AOB+∠DOE=180°-∠DOE+∠DOE=
180°.
7.【答案】
(1)解:如图,
∵OB平分∠DOF
∴∠BOD=∠BOF=40°
又∵∠AOC与∠BOD互为对顶角
∴∠AOC=∠BOD=40°
∴∠AOC=40°
(2)解:①
时分成两种情况:
如上图情况:∠AOE=∠AOC+∠COE=x°+60°
如上图情况:∠AOE=∠COE-∠AOC=60°-x°
②
时也分成两种情况:
如上图情况:∠AOE=∠AOC-∠COE=x°-60°
如上图情况:∠AOE=∠AOC+∠COE=x°+60°
综上所述:当
时,∠AOE为60°-x°或60°+x°
当
时,∠AOE为x°-60°或60°+x°
8.【答案】
(1)解:
,
分别为线段
,
中点,
,
,
.
(2)解:由(
)知:
,
,
∵
(3)解:
是
平分线,
是
平分线,
,
,
∴
,
∵
,
∴
当
的大小发生改变,
的大小不发生改变,恒为
.
9.【答案】
(1)解:根据题意,
,
∴点P从点A运动到点B需要:
秒;
∴当t=2时,
;
当t=6时,
;
故答案为:4,8.
(2)
或
(3)解:∵AP=6,
当2t=6时,解得:t=3;
当20-2t=6时,解得:t=7
(4)解:∵AB=10,
①当
时,
;
②当
时,
;
③当
时,
;
④当
时,
;
综上所述,t的值为:
或
或
或
.
10.【答案】
(1)145°;40°;∠ACB+∠DCE=180°
(2)∠DAB+∠CAE=120°,
理由:∵∠DAB=∠DAC+∠CAB=60°+∠CAB,
∴∠DAB+∠CAE=60°+∠CAB+∠CAE=60°+∠EAB=120°;
(3)∠AOD+∠BOC=α+β,
理由:∵∠AOD=∠DOC+∠COA=β+∠COA,
∴∠AOD+∠BOC=β+∠COA+∠BOC=β+∠AOB=α+β.
11.【答案】
(1)6;6
(2)解:DE的长不会改变,理由如下:
∵
点D是线段AC的中点
∴?
∵
点E是线段BC的中点
∴?
∴?
DE
=
DC+CE
∴DE的长不会改变
(3)解:∵
OD平分∠AOC,
OE平分∠BOC
∴
,
∴
∴∠DOE的度数与射线OC的位置无关
12.【答案】
(1)∵BC=15,点C对应的数是10,
∴c-b=15,
∴b=-5,
∵c-b=b-a=15,
∴a=-20;
(2)①∵OQ=10+t,OP=20+2t,
∴PQ=(10+t)+(
20+2t)=30+3t;
∵OB=5,
OQ=10+t,
∴BQ=15+t,
∵M为BQ的中点,
∴BM=7.5+0.5t,
∴OM=7.5+0.5t-5=2.5+0.5t.
∵OP=20+2t,
N为OP的中点,
∴ON=10+t,
∴MN=OM+ON=12.5+1.5t;
②PQ-2MN=5.
∵PQ=30+3t,MN=
12.5+1.5t,
∴PQ-2MN=(30+3t)-2(12.5+1.5t)=5.
13.【答案】
(1)解:∵线段AC=10厘米,BC=6厘米,点M,N分别是AC,BC的中点,
∴CM=
AC=5厘米,CN=
BC=3厘米,
∴MN=CM+CN=8厘米;
(2)解:∵点M,N分别是AC,BC的中点,
∴CM=
AC,CN=
BC,
∴MN=CM+CN=
AC+
BC=
a;
(3)解:①当0<t≤5时,C是线段PQ的中点,得
10﹣2t=6﹣t,解得t=4;
②当5<t≤
时,P为线段CQ的中点,2t﹣10=16﹣3t,解得t=
;
③当
<t≤6时,Q为线段PC的中点,6﹣t=3t﹣16,解得t=
;
④当6<t≤8时,C为线段PQ的中点,2t﹣10=t﹣6,解得t=4(舍),
综上所述:t=4或
或
.
14.【答案】
(1)【解答】∵∠ECB=90°,∠DCE=25°
∴∠DCB=90°﹣25°=65°
∵∠ACD=90°
∴∠ACB=∠ACD+∠DCB=155°.
∵∠ACB=150°,∠ACD=90°
∴∠DCB=150°﹣90°=60°
∵∠ECB=90°
∴∠DCE=90°﹣60°=30°.
故答案为:155°,30°
(2)【解答】猜想得:∠ACB+∠DCE=180°(或∠ACB与∠DCE互补)
理由:∵∠ECB=90°,∠ACD=90°
∴∠ACB=∠ACD+∠DCB=90°+∠DCB
∠DCE=∠ECB﹣∠DCB=90°﹣∠DCB
∴∠ACB+∠DCE=180°
(3)【解答】∠DAB+∠CAE=120°
理由如下:
∵∠DAB=∠DAE+∠CAE+∠CAB
故∠DAB+∠CAE=∠DAE+∠CAE+∠CAB+∠CAE=∠DAC+∠BAE=120°.
15.【答案】
(1)解:∠ACE=∠BCD,理由如下:
∵∠ACD=∠BCE=90°,∠ACE+∠ECD=∠ECB+∠ECD=90°,
∴∠ACE=∠BCD;
(2)解:若∠DCE=30°,∠ACD=90°,
∴∠ACE=∠ACD﹣∠DCE=90°﹣30°=60°,
∵∠BCE=90°且∠ACB=∠ACE+∠BCE,
∠ACB=90°+60°=150°
(3)解:猜想∠ACB+∠DCE=180°.理由如下:
∵∠ACD=90°=∠ECB,∠ACD+∠ECB+∠ACB+∠DCE=360°,
∴∠ECD+∠ACB=360°﹣(∠ACD+∠ECB)=360°﹣180°=180°
(4)解:成立.
16.【答案】
(1)【解答】如图①两条直线交于一点,图中共有
=2对对顶角;如图②三条直线交于一点,图中共有
=6对对顶角;如图③四条直线交于一点,图中共有
=12对对顶角;
…;
按这样的规律,10条直线交于一点,那么对顶角共有:
=90,
故答案为:90
(2)【解答】由(1)得:n(n≥2)条直线交于一点,对顶角有:
=n(n﹣1).
故答案为:n(n﹣1).
17.【答案】
(1)∠AOD=∠BOC;∠BOP=∠COP
(2)40°;20°;50°
18.【答案】
(1)点B表示的数是﹣6;点P表示的数是8﹣5t
(2)解:设点P运动x秒时,在点C处追上点Q
(如图)
则AC=5x,BC=3x,
∵AC﹣BC=AB
∴5x﹣3x=14…
解得:x=7,
∴点P运动7秒时,在点C处追上点Q
(3)解:没有变化.分两种情况:
①当点P在点A.B两点之间运动时:
MN=MP+NP=
AP+
BP=
(AP+BP)=
AB=7…
②当点P运动到点B的左侧时:
MN=MP﹣NP=
AP﹣
BP=
(AP﹣BP)=
AB=7…
综上所述,线段MN的长度不发生变化,其值为7…
(4)解:式子|x+6|+|x﹣8|有最小值,最小值为14.…
19.【答案】
(1)解:①∵∠COD=90°,∠DOE=25°,
∴∠COE=∠COD﹣∠DOE=90°﹣25°=65°,
又∵OE平分∠BOC,
∴∠BOC=2∠COE=130°,
∴∠AOC=180°﹣∠BOC=180°﹣130°=50°;
②∵∠COD=90°,∠DOE=α,
∴∠COE=∠COD﹣∠DOE=90°﹣α,
又∵OE平分∠BOC,
∴∠BOC=2∠COE=180°﹣2α,
∴∠AOC=180°﹣∠BOC=180°﹣(180°﹣2α)=2α
(2)解:∠DOE=
∠AOC,理由如下:
∵∠BOC=180°﹣∠AOC,
又∵OE平分∠BOC
∴∠COE=
∠BOC=
(180°﹣∠AOC)=90°﹣
∠AOC,
又∵∠COD=90°,
∴∠DOE=90°﹣∠COE=90°﹣(90°﹣
∠AOC)=
∠AOC
20.【答案】
(1)解:如图1,
∵∠AOC与∠BOC互余,
∴∠AOC+∠BOC=90°,
∵∠AOC=40°,
∴∠BOC=50°,
∵OC平分∠MOB,
∴∠MOC=∠BOC=50°,
∴∠BOM=100°,
∵∠MON=40°,
∴∠BON=∠MON-∠BOM=140°-100°=40°,
(2)解:β=2α-40°,理由是:
如图1,∵∠AOC=α,
∴∠BOC=90°-α,
∵OC平分∠MOB,
∴∠MOB=2∠BOC=2(90°-α)=180°-2α,
又∵∠MON=∠BOM+∠BON,
∴140°=180°-2α+β,即β=2α-40°;
(3)解:不成立,此时此时α与β之间的数量关系为:2α+β=40°,
理由是:如图2,
∵∠AOC=α,∠NOB=β,
∴∠BOC=90°-α,
∵OC平分∠MOB,
∴∠MOB=2∠BOC=2(90°-α)=180°-2α,
∵∠BOM=∠MON+∠BON,
∴180°-2α=140°+β,即2α+β=40°,
答:不成立,此时此时α与β之间的数量关系为:2α+β=40.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
图形初步认识压轴题专项训练
1.已知:直线AB与直线CD交于点O,过点O作OE⊥AB.
(1)如图1,OP为∠AOD内的一条射线,若∠1=∠2,求证:OP⊥CD;
(2)如图2,若∠BOC=2∠AOC,求∠COE的度数;
(3)如图3.在(2)的条件下,过点O作OF⊥CD,经过点O画直线MN,若射线OM平分∠BOD,请直接写出图中与2∠EOF度数相等的角.
2.如图①,已知OC是∠AOB内部的一条射线,M、N分别为OA、OB上的点,线段OM、ON同时开始旋转,线段OM以30度/秒绕点O逆时针旋转,线段ON以10度/秒的速度绕点O顺时针旋转,当OM旋转到与OB重合时,线段OM、ON都停止旋转.设OM的旋转时间为t秒.
(1)若∠AOB=140°,当t=2秒时,∠MON=________,当t=4秒时,∠MON=________;
(2)如图②,若∠AOB=140°,OC是∠AOB的平分线,求t为何值时,两个角∠NOB与∠COM中的其中一个角是另一个角的2倍.
(3)如图③,若OM、ON分别在∠AOC、∠COB内部旋转时,总有∠COM=3∠CON,请直接写出
的值.
3.已知直线AB与CD相交于点O,且∠AOD=90°,现将一个直角三角尺的直角顶点放在点O处,把该直角三角尺OEF绕着点O旋转,作射线OH平分∠AOE.
(1)如图1所示,当∠DOE=20°时,∠FOH的度数是________.
(2)若将直角三角尺OEF绕点O旋转至图2的位置,试判断∠FOH和∠BOE之间的数量关系,并说明理由.
(3)若再作射线OG平分∠BOF,试求∠GOH的度数.
4.综合与探究
(实践操作)三角尺中的数学
数学实践活动课上,“奋进”小组将一副直角三角尺的直角顶点叠放在一起,如图1,使直角顶点重合于点C.
(1)(问题发现)
①填空:如图1,若∠ACB=145°,则∠ACE的度数是________,∠DCB的度数________,∠ECD的度数是________.
②如图1,你发现∠ACE与∠DCB的大小有何关系?________;∠ACB与∠ECD的大小又有何关系?________。
(2)(类比探究)
如图2,当△ACD与△BCE没有重合部分时,上述②中你发现的结论是否还依然成立?请说明理由.
5.定义:若
,且
,则我们称
是
的差余角.例如:若
,则
的差余角
.
(1)如图1,点O在直线
上,射线
是
的角平分线,若
是
的差余角,求
的度数.
(2)如图2,点O在直线
上,若
是
的差余角,那么
与
有什么数量关系.
(3)如图3,点O在直线
上,若
是
的差余角,且
与
在直线
的同侧,请你探究
是否为定值?若是,请求出定值;若不是,请说明理由.
6.如图,已知
和
都是直角,它们有公共顶点O.
(1)若
,求
的度数.
(2)判断
和
的大小关系,并说明理由.
(3)猜想:
和
有怎样的数量关系,并说明理由.
7.已知,直线AB与直线CD相交于O,OB平分∠DOF.
(1)如图,若∠BOF=40°,求∠AOC的度数;
(2)作射线OE,使得∠COE=60°,若∠BOF=x°(
),求∠AOE的度数(用含x的代数式表示).
8.(1)如图1,点
在线段
上,
,
,点
,
分别是线段
,
的中点.求线段
的长;
(2)点
在线段
上,若
,点
,
分别是线段
,
的中点.你能得出
的长度吗?并说明理由.
(3)类似的,如图2,
是直角,射线
在
外部,且
是锐角,
是
的平分线,
是
的平分线.当
的大小发生改变时,
的大小也会发生改变吗?为什么?
9.点A
,
B在数轴上表示的数如图所示.动点P从点A出发,沿数轴向右以每秒2个单位长度的速度运动到点B
,
再从点B以同样的速度运动到点A停止,设点P运动的时间为t秒,解答下列问题.
(1)当t=2时,AP=个单位长度,当t=6时,AP=个单位长度;
(2)直接写出整个运动过程中AP的长度(用含t的代数式表示);
(3)当AP=6个单位长度时,求t的值;
(4)当点P运动到线段AB的3等分点时,t的值为.
10.如图(a),将两块直角三角尺的直角顶点C叠放在一起.
(1)若∠DCE=35°,∠ACB=________;若∠ACB=140°,则∠DCE=________;并猜想∠ACB与∠DCE的大小有何特殊关系,并说明理由________;
(2)如图(b),若是两个同样的三角尺60°锐角的顶点A重合在一起,则∠DAB与∠CAE的大小有何关系,请说明理由;
(3)已知∠AOB=α,∠COD=β(都是锐角),如图(c),若把它们的顶点O重合在一起,请直接写出∠AOD与∠BOC的大小相等的关系(用含有α,β的式子表示).
11.如图①,已知线段AB=12cm,点C为线段AB上的一个动点,点D、E分别是AC和BC的中点.
(1)若点C恰好是AB的中点,则DE=________cm;若AC=4cm,则DE=________cm;
(2)随着C点位置的改变,DE的长是否会改变?如果改变,请说明原因;如果不变,请求出DE的长;
(3)知识迁移:如图②,已知∠AOB=120°,过角的内部任意一点C画射线OC,若O
D、OE分别平分∠AOC和∠BOC,试说明∠DOE的度数与射线OC的位置无关.
12.如图1,已知数轴上有三点A、B、C,它们对应的数分别为a、b、c,且c-b=b-a;点C对应的数是10.
(1)若BC=15,
求a、b的值;
(2)如图2,在(1)的条件下,O为原点,动点P、Q分别从A、C同时出发,点P向左运动,运动速度为2个单位长度/秒,点Q向右运动,运动速度为1个单位长度/秒,N为OP的中点,M为BQ的中点.
①用含t代数式表示PQ、
MN;
②在P、Q的运动过程中,PQ与MN存在一个确定的等量关系,请指出他们之间的关系,并说明理由.
13.如图1,已知点C在线段AB上,线段AC=10厘米,BC=6厘米,点M,N分别是AC,BC的中点.
(1)求线段MN的长度;
(2)根据第(1)题的计算过程和结果,设AC+BC=a,其他条件不变,求MN的长度;
(3)动点P、Q分别从A、B同时出发,点P以2cm/s的速度沿AB向右运动,终点为B,点Q以1cm/s的速度沿AB向左运动,终点为A,当一个点到达终点,另一个点也随之停止运动,求运动多少秒时,C、P、Q三点有一点恰好是以另两点为端点的线段的中点?
14.如图(1),将两块直角三角尺的直角顶点C叠放在一起,
(1)若∠DCE=25°,∠ACB=?;若∠ACB=150°,则∠DCE=?;
(2)猜想∠ACB与∠DCE的大小有何特殊关系,并说明理由;
(3)如图(2),若是两个同样的直角三角尺60°锐角的顶点A重合在一起,则∠DAB与∠CAE的大小又有何关系,请说明理由.
15.如图(1),将两块直角三角板的直角顶点C叠放在一起.
(1)试判断∠ACE与∠BCD的大小关系,并说明理由;
(2)若∠DCE=30°,求∠ACB的度数;
(3)猜想∠ACB与∠DCE的数量关系,并说明理由;
(4)若改变其中一个三角板的位置,如图(2),则第(3)小题的结论还成立吗?(不需说明理由)
16.我们知道两直线交于一点,对顶角有2对,三条直线交于一点,对顶角有6对,四条直线交于一点,对顶角有12对,…
(1)10条直线交于一点,对顶角有多少对?
(2)n(n≥2)条直线交于一点,对顶角有多少对?
17.如图,直线AB与CD相交于点O,OP是∠BOC的平分线,OE⊥AB,OF⊥CD,
(1)图中除直角外,还有相等的角吗?请写出两对:①________;②________
.
(2)如果∠AOD=40°,则①∠BOC=________;②OP是∠BOC的平分线,所以∠COP=________度;③求∠BOF的度数________?.
18.如图,已知数轴上点A表示的数为8,B是数轴上一点,且AB=14.动点P从点A出发,以每秒5个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒.
(1)写出数轴上点B表示的数________
,
点P表示的数________(用含t的代数式表示);
(2)动点Q从点B出发,以每秒3个单位长度的速度沿数轴向左匀速运动,若点P、Q同时出发,问点P运动多少秒时追上点Q?
(3)若M为AP的中点,N为PB的中点.点P在运动的过程中,线段MN的长度是否发生变化?若变化,请说明理由;若不变,请你画出图形,并求出线段MN的长;
(4)若点D是数轴上一点,点D表示的数是x,请你探索式子|x+6|+|x﹣8|是否有最小值?如果有,直接写出最小值;如果没有,说明理由.
19.点
O
是直线
AB上一点,∠COD
是直角,OE平分∠BOC.
(1)①如图1,若∠DOE=25°,求∠AOC
的度数;
②如图2,若∠DOE=α,直接写出∠AOC的度数(用含α的式子表示);
(2)将图
1中的∠COD
绕点O按顺时针方向旋转至图
2
所示位置.探究∠DOE
与∠AOC
的度数之间的关系,写出你的结论,并说明理由.
20.如图1,已知∠MON=140°,∠AOC与∠BOC互余,OC平分∠MOB,
(1)在图1中,若∠AOC=40°,则∠BOC=°,∠NOB=°.
(2)在图1中,设∠AOC=α,∠NOB=β,请探究α与β之间的数量关系(必须写出推理的主要过程,但每一步后面不必写出理由);
(3)在已知条件不变的前提下,当∠AOB绕着点O顺时针转动到如图2的位置,此时α与β之间的数量关系是否还成立?若成立,请说明理由;若不成立,请直接写出此时α与β之间的数量关系.
答案解析部分
一、综合题
1.【答案】
(1)解:∵OE⊥AB
∴∠AOC+∠1=
∵∠1=∠2
∴∠AOC+∠2=
∴OP⊥CD
(2)解:∵∠AOC+∠BOC=
,且∠BOC=2∠AOC
∴∠AOC=
∵OE⊥AB
∴∠AOE=
∴∠COE=
-
=
(3)∠AOD、∠BOC、∠FON、∠EOM
2.【答案】
(1)60°;20°
(2)解:若∠COM=2∠BON时,|30°t﹣70°|=2×10°×t,
∴t=
或7(不合题意舍去)
当∠BON=2∠COM时,2|30°t﹣70°|=10°×t,
∴t=2或
,
综上所述当t=
或2或
时,两个角∠NOB与∠COM中的其中一个角是另一个角的2倍.
(3)解:∵∠COM=3∠CON,
∴∠AOB﹣∠BOC﹣30°×t=3(∠BOC﹣10°×t),
∴∠AOB=4∠BOC,
∴
=
.
3.【答案】
(1)35°
(2)解:∠BOE=2∠FOH,理由如下:
设∠AOH=x,
因为OH平分∠AOE
所以∠HOE=∠AOH=x
所以∠FOH=90
°﹣∠HOE=90°﹣x
∠BOE=180°﹣∠AOE=180°﹣2x
所以∠BOE=2∠FOH;
(3)解:如图3,当OE落在∠BOD内时,OF落在∠AOD内
因为OH平分∠AOE
所以∠HOE=∠AOH=
AOE
因为OG平分∠BOF
∠FOG=∠GOB=
BOF
所以∠GOH=∠GOF﹣∠FOH
=
BOF﹣(∠AOH﹣∠AOF)
=
(180°﹣∠AOF)﹣
AOE+∠AOF
=90°﹣
AOF﹣
(90°+∠AOF)+∠AOF
=90°﹣
AOF﹣45°﹣
AOF+∠AOF
=45°;
所以∠GOH的度数为45°;
如图4,当OE落在其他位置时
因为OH平分∠AOE
所以∠HOE=∠AOH=
AOE
因为OG平分∠BOF
∠FOG=∠GOB=
BOF
所以∠GOH=∠GOF+∠FOH
=
BOF+∠AOH+∠AOF
=
(180°﹣∠AOF)+
AOE+∠AOF
=90°﹣
AOF+
(90°﹣∠AOF)+∠AOF
=90°﹣
AOF+45°﹣
AOF+∠AOF
=135°;
所以∠GOH的度数为135°
综上所述:∠GOH的度数为45°
或135°.
4.【答案】
(1)5°;55°;35°;∠ACE=∠DCB;∠ACB+∠ECD=180°;
(2)解:结论:当
与
没有重合部分时,上述②中发现的结论依然成立.
理由:∵
,
∴
,
∴
,
∵
,
∴
,
∵
,
∴
,
∴
,
.
∴上述②中发现的结论依然成立.
5.【答案】
(1)解:如图,∵
是
的差余角
∴
-
=90°,
即
=
+90°,
又∵
是
的角平分线,
∴∠BOE=
,
则
+90°+
+
=180°,
解得
=30°;
(2)解:∵
是
的差余角,
∴
-
=90°,
∵
=
+
,
=
+
,
∴
-
=90°,
∵
=180°-
,
∴180°-
-
=90°,
∴
+
=90°;
(3)解:当OE在OC左侧时,
∵
是
的差余角,
∴
-
=90°,
∴∠AOE=∠BOE=90°,
则
=
=
=2;
当OE在OC右侧时,
过点O作OF⊥AB,
∵
是
的差余角,
∴
=90°+
,
又∵
=90°+
,
∴
=
,
∴
=
=
=
=
=2.
综上:
为定值2.
6.【答案】
(1)解:∵∠AOE=∠AOD-∠DOE=90°-60°=30°,
∴∠AOB=∠AOE+∠BOE=30°+90°=120°;
(2)解:相等,理由如下:
∵∠AOE=∠AOD-∠DOE=90°-∠DOE,
∠BOD=∠BOE-∠DOE=90°-∠DOE,
∴∠AOE=∠BOD
;
(3)解:∠AOB+∠DOE=180°,理由如下:
∵
∠AOB=∠AOE+∠BOE
=∠AOD-∠DOE+∠BOE
=90°+90°-∠DOE
=180°-∠DOE
,
∴∠AOB+∠DOE=180°-∠DOE+∠DOE=
180°.
7.【答案】
(1)解:如图,
∵OB平分∠DOF
∴∠BOD=∠BOF=40°
又∵∠AOC与∠BOD互为对顶角
∴∠AOC=∠BOD=40°
∴∠AOC=40°
(2)解:①
时分成两种情况:
如上图情况:∠AOE=∠AOC+∠COE=x°+60°
如上图情况:∠AOE=∠COE-∠AOC=60°-x°
②
时也分成两种情况:
如上图情况:∠AOE=∠AOC-∠COE=x°-60°
如上图情况:∠AOE=∠AOC+∠COE=x°+60°
综上所述:当
时,∠AOE为60°-x°或60°+x°
当
时,∠AOE为x°-60°或60°+x°
8.【答案】
(1)解:
,
分别为线段
,
中点,
,
,
.
(2)解:由(
)知:
,
,
∵
(3)解:
是
平分线,
是
平分线,
,
,
∴
,
∵
,
∴
当
的大小发生改变,
的大小不发生改变,恒为
.
9.【答案】
(1)解:根据题意,
,
∴点P从点A运动到点B需要:
秒;
∴当t=2时,
;
当t=6时,
;
故答案为:4,8.
(2)
或
(3)解:∵AP=6,
当2t=6时,解得:t=3;
当20-2t=6时,解得:t=7
(4)解:∵AB=10,
①当
时,
;
②当
时,
;
③当
时,
;
④当
时,
;
综上所述,t的值为:
或
或
或
.
10.【答案】
(1)145°;40°;∠ACB+∠DCE=180°
(2)∠DAB+∠CAE=120°,
理由:∵∠DAB=∠DAC+∠CAB=60°+∠CAB,
∴∠DAB+∠CAE=60°+∠CAB+∠CAE=60°+∠EAB=120°;
(3)∠AOD+∠BOC=α+β,
理由:∵∠AOD=∠DOC+∠COA=β+∠COA,
∴∠AOD+∠BOC=β+∠COA+∠BOC=β+∠AOB=α+β.
11.【答案】
(1)6;6
(2)解:DE的长不会改变,理由如下:
∵
点D是线段AC的中点
∴?
∵
点E是线段BC的中点
∴?
∴?
DE
=
DC+CE
∴DE的长不会改变
(3)解:∵
OD平分∠AOC,
OE平分∠BOC
∴
,
∴
∴∠DOE的度数与射线OC的位置无关
12.【答案】
(1)∵BC=15,点C对应的数是10,
∴c-b=15,
∴b=-5,
∵c-b=b-a=15,
∴a=-20;
(2)①∵OQ=10+t,OP=20+2t,
∴PQ=(10+t)+(
20+2t)=30+3t;
∵OB=5,
OQ=10+t,
∴BQ=15+t,
∵M为BQ的中点,
∴BM=7.5+0.5t,
∴OM=7.5+0.5t-5=2.5+0.5t.
∵OP=20+2t,
N为OP的中点,
∴ON=10+t,
∴MN=OM+ON=12.5+1.5t;
②PQ-2MN=5.
∵PQ=30+3t,MN=
12.5+1.5t,
∴PQ-2MN=(30+3t)-2(12.5+1.5t)=5.
13.【答案】
(1)解:∵线段AC=10厘米,BC=6厘米,点M,N分别是AC,BC的中点,
∴CM=
AC=5厘米,CN=
BC=3厘米,
∴MN=CM+CN=8厘米;
(2)解:∵点M,N分别是AC,BC的中点,
∴CM=
AC,CN=
BC,
∴MN=CM+CN=
AC+
BC=
a;
(3)解:①当0<t≤5时,C是线段PQ的中点,得
10﹣2t=6﹣t,解得t=4;
②当5<t≤
时,P为线段CQ的中点,2t﹣10=16﹣3t,解得t=
;
③当
<t≤6时,Q为线段PC的中点,6﹣t=3t﹣16,解得t=
;
④当6<t≤8时,C为线段PQ的中点,2t﹣10=t﹣6,解得t=4(舍),
综上所述:t=4或
或
.
14.【答案】
(1)【解答】∵∠ECB=90°,∠DCE=25°
∴∠DCB=90°﹣25°=65°
∵∠ACD=90°
∴∠ACB=∠ACD+∠DCB=155°.
∵∠ACB=150°,∠ACD=90°
∴∠DCB=150°﹣90°=60°
∵∠ECB=90°
∴∠DCE=90°﹣60°=30°.
故答案为:155°,30°
(2)【解答】猜想得:∠ACB+∠DCE=180°(或∠ACB与∠DCE互补)
理由:∵∠ECB=90°,∠ACD=90°
∴∠ACB=∠ACD+∠DCB=90°+∠DCB
∠DCE=∠ECB﹣∠DCB=90°﹣∠DCB
∴∠ACB+∠DCE=180°
(3)【解答】∠DAB+∠CAE=120°
理由如下:
∵∠DAB=∠DAE+∠CAE+∠CAB
故∠DAB+∠CAE=∠DAE+∠CAE+∠CAB+∠CAE=∠DAC+∠BAE=120°.
15.【答案】
(1)解:∠ACE=∠BCD,理由如下:
∵∠ACD=∠BCE=90°,∠ACE+∠ECD=∠ECB+∠ECD=90°,
∴∠ACE=∠BCD;
(2)解:若∠DCE=30°,∠ACD=90°,
∴∠ACE=∠ACD﹣∠DCE=90°﹣30°=60°,
∵∠BCE=90°且∠ACB=∠ACE+∠BCE,
∠ACB=90°+60°=150°
(3)解:猜想∠ACB+∠DCE=180°.理由如下:
∵∠ACD=90°=∠ECB,∠ACD+∠ECB+∠ACB+∠DCE=360°,
∴∠ECD+∠ACB=360°﹣(∠ACD+∠ECB)=360°﹣180°=180°
(4)解:成立.
16.【答案】
(1)【解答】如图①两条直线交于一点,图中共有
=2对对顶角;如图②三条直线交于一点,图中共有
=6对对顶角;如图③四条直线交于一点,图中共有
=12对对顶角;
…;
按这样的规律,10条直线交于一点,那么对顶角共有:
=90,
故答案为:90
(2)【解答】由(1)得:n(n≥2)条直线交于一点,对顶角有:
=n(n﹣1).
故答案为:n(n﹣1).
17.【答案】
(1)∠AOD=∠BOC;∠BOP=∠COP
(2)40°;20°;50°
18.【答案】
(1)点B表示的数是﹣6;点P表示的数是8﹣5t
(2)解:设点P运动x秒时,在点C处追上点Q
(如图)
则AC=5x,BC=3x,
∵AC﹣BC=AB
∴5x﹣3x=14…
解得:x=7,
∴点P运动7秒时,在点C处追上点Q
(3)解:没有变化.分两种情况:
①当点P在点A.B两点之间运动时:
MN=MP+NP=
AP+
BP=
(AP+BP)=
AB=7…
②当点P运动到点B的左侧时:
MN=MP﹣NP=
AP﹣
BP=
(AP﹣BP)=
AB=7…
综上所述,线段MN的长度不发生变化,其值为7…
(4)解:式子|x+6|+|x﹣8|有最小值,最小值为14.…
19.【答案】
(1)解:①∵∠COD=90°,∠DOE=25°,
∴∠COE=∠COD﹣∠DOE=90°﹣25°=65°,
又∵OE平分∠BOC,
∴∠BOC=2∠COE=130°,
∴∠AOC=180°﹣∠BOC=180°﹣130°=50°;
②∵∠COD=90°,∠DOE=α,
∴∠COE=∠COD﹣∠DOE=90°﹣α,
又∵OE平分∠BOC,
∴∠BOC=2∠COE=180°﹣2α,
∴∠AOC=180°﹣∠BOC=180°﹣(180°﹣2α)=2α
(2)解:∠DOE=
∠AOC,理由如下:
∵∠BOC=180°﹣∠AOC,
又∵OE平分∠BOC
∴∠COE=
∠BOC=
(180°﹣∠AOC)=90°﹣
∠AOC,
又∵∠COD=90°,
∴∠DOE=90°﹣∠COE=90°﹣(90°﹣
∠AOC)=
∠AOC
20.【答案】
(1)解:如图1,
∵∠AOC与∠BOC互余,
∴∠AOC+∠BOC=90°,
∵∠AOC=40°,
∴∠BOC=50°,
∵OC平分∠MOB,
∴∠MOC=∠BOC=50°,
∴∠BOM=100°,
∵∠MON=40°,
∴∠BON=∠MON-∠BOM=140°-100°=40°,
(2)解:β=2α-40°,理由是:
如图1,∵∠AOC=α,
∴∠BOC=90°-α,
∵OC平分∠MOB,
∴∠MOB=2∠BOC=2(90°-α)=180°-2α,
又∵∠MON=∠BOM+∠BON,
∴140°=180°-2α+β,即β=2α-40°;
(3)解:不成立,此时此时α与β之间的数量关系为:2α+β=40°,
理由是:如图2,
∵∠AOC=α,∠NOB=β,
∴∠BOC=90°-α,
∵OC平分∠MOB,
∴∠MOB=2∠BOC=2(90°-α)=180°-2α,
∵∠BOM=∠MON+∠BON,
∴180°-2α=140°+β,即2α+β=40°,
答:不成立,此时此时α与β之间的数量关系为:2α+β=40.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
