华东师大版九年级数学下册第26章26.2.2二次函数的图象与性质 第3课时 -课件(21张PPT)
文档属性
| 名称 | 华东师大版九年级数学下册第26章26.2.2二次函数的图象与性质 第3课时 -课件(21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-19 22:56:56 | ||
图片预览





文档简介
一、复习回顾
1.二次函数y=-2x2的图象是________,它的开口方向________,顶点坐标是________,对称轴是________,在对称轴的左侧,y随x的增大而________,在对称轴的右侧,y随x的增大而________,当x=________时,函数有________值,其最值为________.
抛物线
向下
( 0,0 )
减小
增大
0
最大
0
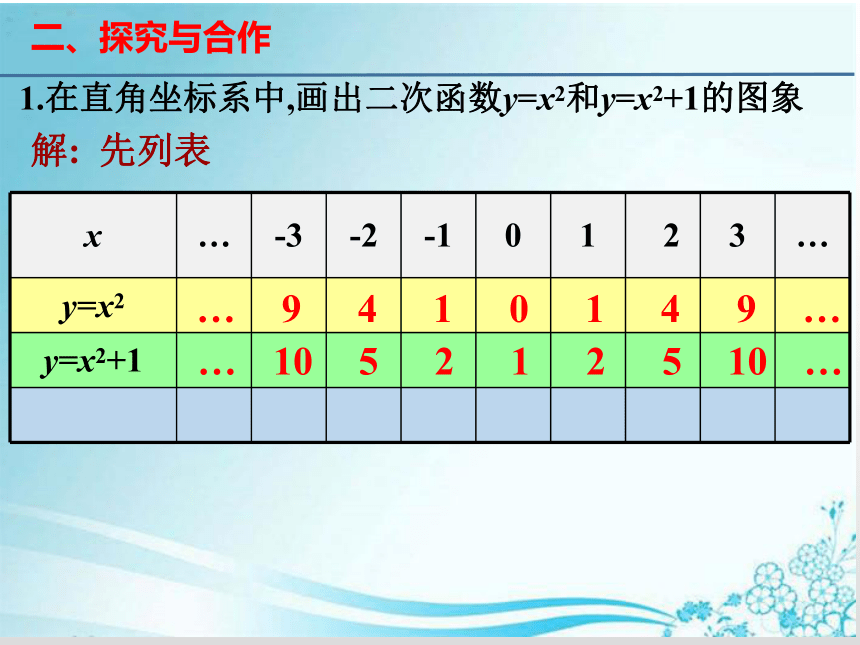
1.在直角坐标系中,画出二次函数y=x2和y=x2+1的图象
解: 先列表
x
…
-3
-2
-1
0
1
2
3
…
y=x2
y=x2+1
…
9
4
1
0
1
4
9
…
二、探究与合作
…
10
5
2
1
2
5
10
…
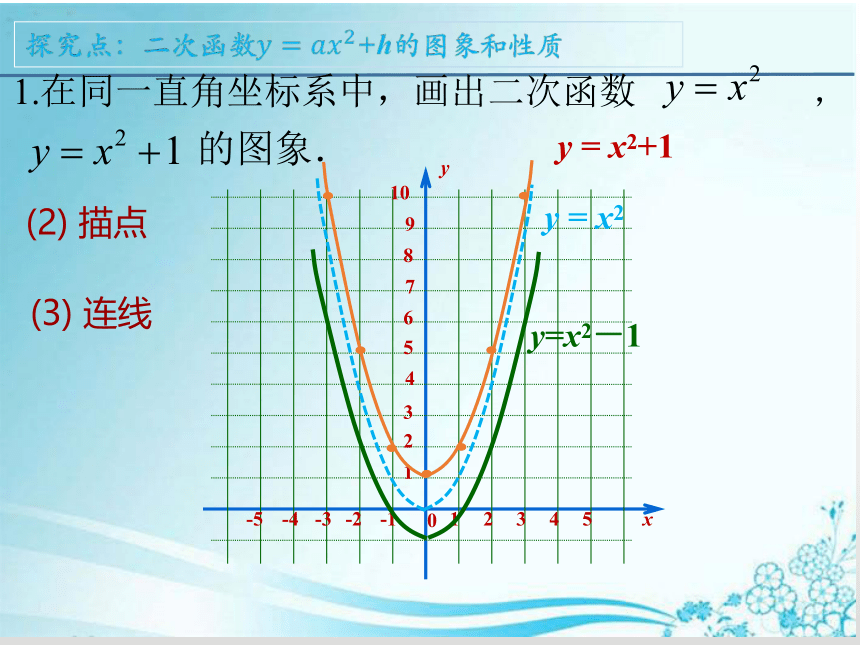
(2) 描点
1
2
3
4
5
x
1
2
3
4
5
6
7
8
9
10
y
0
-1
-2
-3
-4
-5
y = x2+1
?
,
1.在同一直角坐标系中,画出二次函数
的图象.
y = x2
y=x2-1
(3) 连线
1
2
3
4
5
x
1
2
3
4
5
6
7
8
9
10
y
o
-1
-2
-3
-4
-5
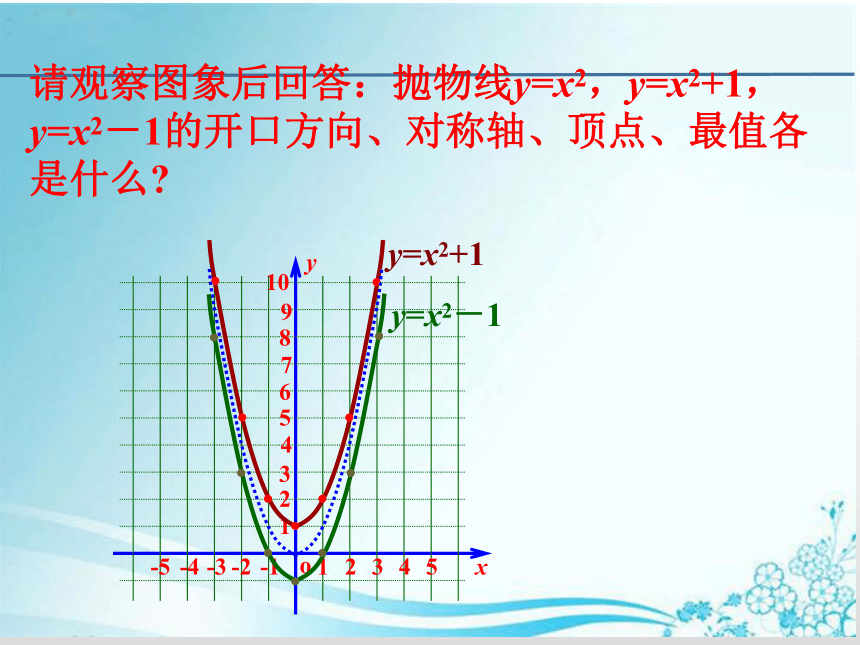
请观察图象后回答:抛物线y=x2,y=x2+1,y=x2-1的开口方向、对称轴、顶点、最值各是什么?
y=x2+1
y=x2-1
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}?
开口方向
顶点
对称轴
有最高(低)点
最值
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
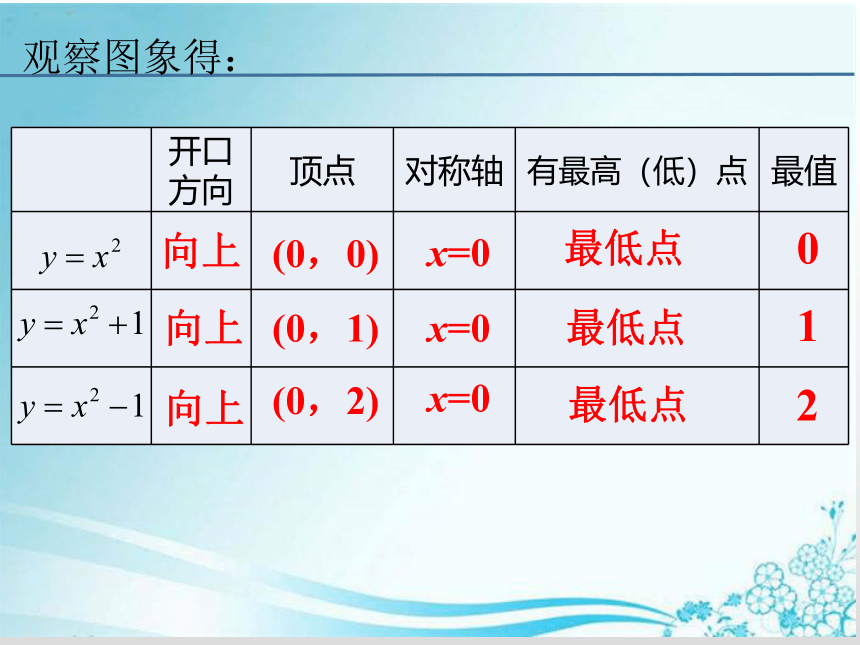
观察图象得:
向上
向上
向上
(0,0)
(0,1)
(0,2)
x=0
x=0
x=0
最低点
最低点
最低点
0
1
2
(2)将抛物线y=x2向 平移 个单位长度得抛物线y=x2+1;
(3)将抛物线y=x2向 平移 个单位长度得抛物线y=x2-1.
上
1
下
1
(1)抛物线y=x2+1,y=x2-1与抛物线y=x2的形状_____________
相同
讨论:抛物线y=x2+1,y=x2-1与抛物线y=x2有什么关系?
小结:抛物线上下平移的规律及y=ax2+k的图象与性质:
(1)抛物线y=ax2向上平移k(k>0)个单位长度,可得到的抛物线函数表达式为 .
(2)抛物线y=ax2向下平移k(k>0)个单位长度,可得到的抛物线函数表达式为 .
(3)抛物线y=ax2+k的图象性质:①当a>0,开口 ;当a<0,开口 ;②顶点坐标为
;③对称轴为 .
y=ax2+k
y=ax2-k
向上
向下
(0,k)
直线x=0
快速填空1:
向下
向下
直线x=0(或y轴)
直线x=0(或y轴)
(0,0)
(0,1)
0
大
0
0
大
1
减小
增大
减小
增大
快速填空1:
向上
向上
直线x=0(或y轴)
直线x=0(或y轴)
快速填空2:
(0,0)
(0,-1)
0
小
0
0
小
-1
增大
减小
增大
减小
快速填空2:
1.把抛物线 向下平移2个单位,可以得到抛物线 ,再向上平移5个单位,可以得到抛物线 ;
2.抛物线 的开口 ,对称轴是 ,顶点坐标是 ,当x= 时,取得最 值,这个值等于 。当x____ 时, y随x的增大而增大, 当x 时, y随x的增大而减小.
向下
y轴
(0,-3)
<0
>0
小试牛刀
0
大
-3
1.抛物线 y=ax2+c与y=-5x2的形状大小、开口方向相同,且顶点坐标是(0,3),则其表达式为_____________,它是由抛物线y=-5x2向________平移________个单位得到的.
2.与抛物线y=- x2+1顶点相同,对称轴相同,但开口方向相反的抛物线是 .
3.下列函数中,当x>0时,y随x的增大而增大的是( )
A.y=-2x B.y=x2-1
C.y=-x+1 D.y=-7x2
及时反馈
4.在同一坐标系中,一次函数y=ax+1和二次函数y=x2+a的图象可能是( )
5.若抛物线y=ax2+c与y=-2x2+5关于x轴对称,求a,c的值.
解: ∵两抛物线关于x轴对称
?
?
6.若二次函数
与二次函数
图象的形状完全相同,则
与
的关系为( )
A.
=
B.
=
C.
=
D.无法判断
7.若二次函数
的开口方向
向下,则m的取值范围为 .
8.将二次函数
图象向下平移5个
单位得到的抛物线的顶点坐标为 .
9.把抛物线
沿 y
轴向下平移
,则
,
.
7个单位得到的抛物线的解析式为
?
(0,-6)
3
3
1.已知二次函数y=3x2+4,点A(x1,y1),B(x2,y2),
在其图象上,且x1< x2<0,
则 y1、y2的大 小关系为________
x1
x2
y1
y2
拓展提升
2.已知二次函数y=ax2+c ,当x取x1,x2(x1≠x2,
x1,x2分别是A,B两点的横坐标)时,函数值相等,
则当x取x1+x2时,函数值为 ( )
A. a+c B. a-c C. –c D. c
D
拓展提升
3.函数y=ax2-a与y=
在同一直角坐标系中的图象可能是 ( )
A
4.将抛物线y=x2+1的图象绕顶点旋转1800,则旋转后的抛物线的函数关系式是________,如果是绕原点O旋转1800,则旋转后的抛物线的函数关系式是________.
y= -x2+1
y= -x2-1
拓展提升
1.二次函数y=-2x2的图象是________,它的开口方向________,顶点坐标是________,对称轴是________,在对称轴的左侧,y随x的增大而________,在对称轴的右侧,y随x的增大而________,当x=________时,函数有________值,其最值为________.
抛物线
向下
( 0,0 )
减小
增大
0
最大
0
1.在直角坐标系中,画出二次函数y=x2和y=x2+1的图象
解: 先列表
x
…
-3
-2
-1
0
1
2
3
…
y=x2
y=x2+1
…
9
4
1
0
1
4
9
…
二、探究与合作
…
10
5
2
1
2
5
10
…
(2) 描点
1
2
3
4
5
x
1
2
3
4
5
6
7
8
9
10
y
0
-1
-2
-3
-4
-5
y = x2+1
?
,
1.在同一直角坐标系中,画出二次函数
的图象.
y = x2
y=x2-1
(3) 连线
1
2
3
4
5
x
1
2
3
4
5
6
7
8
9
10
y
o
-1
-2
-3
-4
-5
请观察图象后回答:抛物线y=x2,y=x2+1,y=x2-1的开口方向、对称轴、顶点、最值各是什么?
y=x2+1
y=x2-1
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}?
开口方向
顶点
对称轴
有最高(低)点
最值
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
观察图象得:
向上
向上
向上
(0,0)
(0,1)
(0,2)
x=0
x=0
x=0
最低点
最低点
最低点
0
1
2
(2)将抛物线y=x2向 平移 个单位长度得抛物线y=x2+1;
(3)将抛物线y=x2向 平移 个单位长度得抛物线y=x2-1.
上
1
下
1
(1)抛物线y=x2+1,y=x2-1与抛物线y=x2的形状_____________
相同
讨论:抛物线y=x2+1,y=x2-1与抛物线y=x2有什么关系?
小结:抛物线上下平移的规律及y=ax2+k的图象与性质:
(1)抛物线y=ax2向上平移k(k>0)个单位长度,可得到的抛物线函数表达式为 .
(2)抛物线y=ax2向下平移k(k>0)个单位长度,可得到的抛物线函数表达式为 .
(3)抛物线y=ax2+k的图象性质:①当a>0,开口 ;当a<0,开口 ;②顶点坐标为
;③对称轴为 .
y=ax2+k
y=ax2-k
向上
向下
(0,k)
直线x=0
快速填空1:
向下
向下
直线x=0(或y轴)
直线x=0(或y轴)
(0,0)
(0,1)
0
大
0
0
大
1
减小
增大
减小
增大
快速填空1:
向上
向上
直线x=0(或y轴)
直线x=0(或y轴)
快速填空2:
(0,0)
(0,-1)
0
小
0
0
小
-1
增大
减小
增大
减小
快速填空2:
1.把抛物线 向下平移2个单位,可以得到抛物线 ,再向上平移5个单位,可以得到抛物线 ;
2.抛物线 的开口 ,对称轴是 ,顶点坐标是 ,当x= 时,取得最 值,这个值等于 。当x____ 时, y随x的增大而增大, 当x 时, y随x的增大而减小.
向下
y轴
(0,-3)
<0
>0
小试牛刀
0
大
-3
1.抛物线 y=ax2+c与y=-5x2的形状大小、开口方向相同,且顶点坐标是(0,3),则其表达式为_____________,它是由抛物线y=-5x2向________平移________个单位得到的.
2.与抛物线y=- x2+1顶点相同,对称轴相同,但开口方向相反的抛物线是 .
3.下列函数中,当x>0时,y随x的增大而增大的是( )
A.y=-2x B.y=x2-1
C.y=-x+1 D.y=-7x2
及时反馈
4.在同一坐标系中,一次函数y=ax+1和二次函数y=x2+a的图象可能是( )
5.若抛物线y=ax2+c与y=-2x2+5关于x轴对称,求a,c的值.
解: ∵两抛物线关于x轴对称
?
?
6.若二次函数
与二次函数
图象的形状完全相同,则
与
的关系为( )
A.
=
B.
=
C.
=
D.无法判断
7.若二次函数
的开口方向
向下,则m的取值范围为 .
8.将二次函数
图象向下平移5个
单位得到的抛物线的顶点坐标为 .
9.把抛物线
沿 y
轴向下平移
,则
,
.
7个单位得到的抛物线的解析式为
?
(0,-6)
3
3
1.已知二次函数y=3x2+4,点A(x1,y1),B(x2,y2),
在其图象上,且x1< x2<0,
则 y1、y2的大 小关系为________
x1
x2
y1
y2
拓展提升
2.已知二次函数y=ax2+c ,当x取x1,x2(x1≠x2,
x1,x2分别是A,B两点的横坐标)时,函数值相等,
则当x取x1+x2时,函数值为 ( )
A. a+c B. a-c C. –c D. c
D
拓展提升
3.函数y=ax2-a与y=
在同一直角坐标系中的图象可能是 ( )
A
4.将抛物线y=x2+1的图象绕顶点旋转1800,则旋转后的抛物线的函数关系式是________,如果是绕原点O旋转1800,则旋转后的抛物线的函数关系式是________.
y= -x2+1
y= -x2-1
拓展提升
