华东师大版九年级数学下册第26章26.2.2二次函数的图象与性质 第4课时 -课件(18张PPT)
文档属性
| 名称 | 华东师大版九年级数学下册第26章26.2.2二次函数的图象与性质 第4课时 -课件(18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-19 22:54:50 | ||
图片预览





文档简介
1.将二次函数y=5x2-3的图象向上平移7个单位后所得抛物线的函数表达式为 __________.
2.写出一个顶点坐标为(0,-3),开口方向与抛物线y=-x2的方向相反,形状相同的抛物线的函数表达式为____________.
3.抛物线y=-x2向 平移 个单位长度,可得到抛物线y=-x2-4.
?
?
温故知新
下
4
【自主检测】
阅读教材第11页至第13页,并完成下列各题.
?
?
?
?
?
?
?
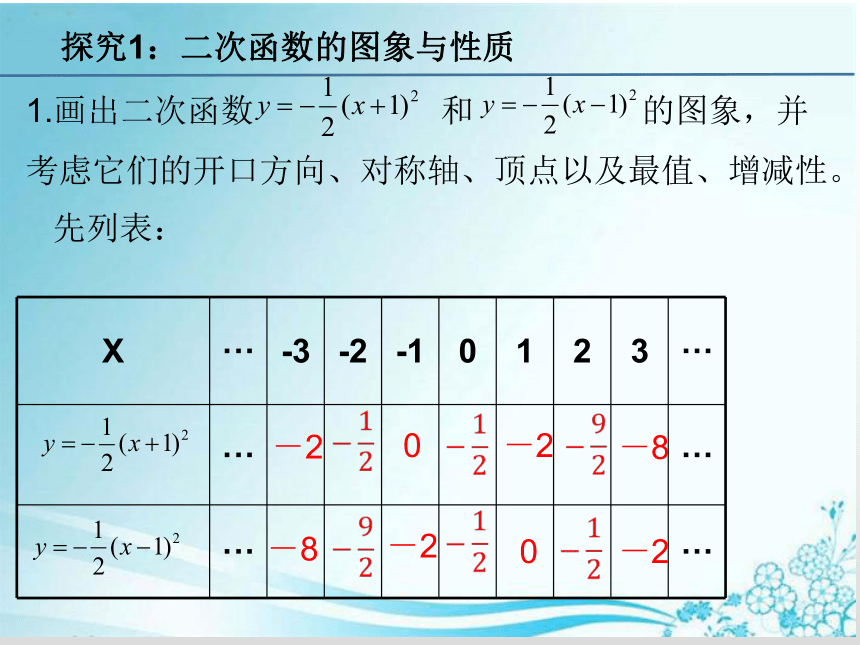
1.画出二次函数 和 的图象,并考虑它们的开口方向、对称轴、顶点以及最值、增减性。
先列表:
X
···
-3
-2
-1
0
1
2
3
···
···
···
···
···
0
-2
-2
0
-2
-2
?
?
?
-8
-8
?
?
?
探究1:二次函数的图象与性质
1
-1
-2
-3
-4
-5
-6
-7
-8
-9
-8
-6
-4
-2
2
4
6
8
y
x
0
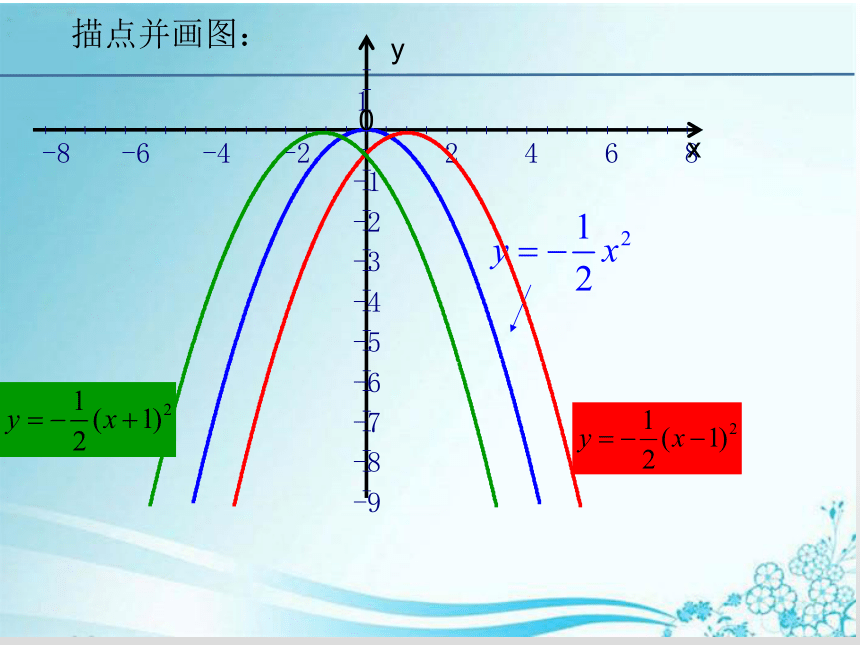
描点并画图:
二、探究与合作
探究点1:二次函数的图象与性质
(1)观察图象,完成下表:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}函数
开口方向
顶点
对称轴
最值
增减性
向下
向下
(-1,0)
(1,0)
?
?
x=-1时,y最大值=0
x=1时,y最大值=0
?
?
二、探究与合作
?
相同
1
1
小结:抛物线左右平移的规律及y=a(x-h)2的图象与性质:
(1)抛物线y=ax2向左平移h(h>0)个单位长度可得到的抛物线表达式为 .
(2)抛物线y=ax2向右平移h(h>0)个单位长度可得到的抛物线表达式为 .
(3)抛物线y=a(x-h)2的图象性质:①当a>0,开口 ;当a<0,开口 ;②顶点坐标为 ;③对称轴为 .
y=a(x+h)2
y=a(x-h)2
向上
向下
(h,0)
直线x=h
1.抛物线y=-3x2向左平移 个单位长度可得到的抛物线表达式为 ;
2.抛物线y=- x2向右平移 个单位长度可得到的抛物线表达式为 .
运用所学
3.二次函数y=-3(x-2)2的图象性质是:
(1)a 0;
(2)开口向 ;
(3)对称轴是 ;
(4)顶点坐标是 ;
(5)当x = 时,y取最 值 ;
(6)当x> 时,y随x的增大而 .
<
下
直线x=2
(2,0)
2
大
0
2
减小
?
向上
?
?
随x增大而增大
最小
0
?
?
?
及时反馈
4. 对于二次函数y=9(x+2)2,下列说法正确的是( )
A. 图象的开口向下
B. 函数有最小值0
C. 当x>-2时,y随x的增大而减小
D. 图象的对称轴是直线x=2
B
5. 在平面直角坐标系中,函数y=-x+1与y=-(x-1)2的图象大致是( )
D
?
<
A
8 抛物线y=-(x-1)2向右平移1个单位长度可得到的抛物线的表达式为 .
9 将一条抛物线向右平移2个单位长度后得到了y=2x2的函数图象,则这条抛物线的表达式是( )
A. y=2x2+2 B. y=2x2-2
C. y=2(x-2)2 D. y=2(x+2)2
y=-(x-2)2
D
10. 如图,抛物线y=a(x+1)2的顶点为A,与y轴的负半轴交于点B,且OB=OA.
(1)求抛物线的表达式;
(2)若点C(-3,b)在该抛物线上,求S△ABC的值.
拓展提升
解:(1)由题意得,A(-1,0),B(0,-1).
将x=0,y=-1代入抛物线表达式,得a=-1.
所以抛物线的表达式为y=-(x+1)2=-x2-2x-1.
(2)如图,过点C作CD⊥x轴交x轴于点D.
将点C(-3,b)代入抛物线表达式,得b=-4,即点C(-3,-4).
S△ABC=S梯形OBCD-S△ACD-S△AOB
11. 如图,抛物线的顶点M在x轴上,抛物线与y轴交于点N,且OM=ON=4.
(1)求抛物线的函数表达式;
解:(1)因为OM=ON=4,
所以M(4,0),N(0,4).
设抛物线的函数表达式为
y=a(x-4)2,
把N(0,4)代入得16a=4,解得
所以抛物线的函数表达式为y= (x-4)2,即y= x2-2x+4.
2.写出一个顶点坐标为(0,-3),开口方向与抛物线y=-x2的方向相反,形状相同的抛物线的函数表达式为____________.
3.抛物线y=-x2向 平移 个单位长度,可得到抛物线y=-x2-4.
?
?
温故知新
下
4
【自主检测】
阅读教材第11页至第13页,并完成下列各题.
?
?
?
?
?
?
?
1.画出二次函数 和 的图象,并考虑它们的开口方向、对称轴、顶点以及最值、增减性。
先列表:
X
···
-3
-2
-1
0
1
2
3
···
···
···
···
···
0
-2
-2
0
-2
-2
?
?
?
-8
-8
?
?
?
探究1:二次函数的图象与性质
1
-1
-2
-3
-4
-5
-6
-7
-8
-9
-8
-6
-4
-2
2
4
6
8
y
x
0
描点并画图:
二、探究与合作
探究点1:二次函数的图象与性质
(1)观察图象,完成下表:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}函数
开口方向
顶点
对称轴
最值
增减性
向下
向下
(-1,0)
(1,0)
?
?
x=-1时,y最大值=0
x=1时,y最大值=0
?
?
二、探究与合作
?
相同
1
1
小结:抛物线左右平移的规律及y=a(x-h)2的图象与性质:
(1)抛物线y=ax2向左平移h(h>0)个单位长度可得到的抛物线表达式为 .
(2)抛物线y=ax2向右平移h(h>0)个单位长度可得到的抛物线表达式为 .
(3)抛物线y=a(x-h)2的图象性质:①当a>0,开口 ;当a<0,开口 ;②顶点坐标为 ;③对称轴为 .
y=a(x+h)2
y=a(x-h)2
向上
向下
(h,0)
直线x=h
1.抛物线y=-3x2向左平移 个单位长度可得到的抛物线表达式为 ;
2.抛物线y=- x2向右平移 个单位长度可得到的抛物线表达式为 .
运用所学
3.二次函数y=-3(x-2)2的图象性质是:
(1)a 0;
(2)开口向 ;
(3)对称轴是 ;
(4)顶点坐标是 ;
(5)当x = 时,y取最 值 ;
(6)当x> 时,y随x的增大而 .
<
下
直线x=2
(2,0)
2
大
0
2
减小
?
向上
?
?
随x增大而增大
最小
0
?
?
?
及时反馈
4. 对于二次函数y=9(x+2)2,下列说法正确的是( )
A. 图象的开口向下
B. 函数有最小值0
C. 当x>-2时,y随x的增大而减小
D. 图象的对称轴是直线x=2
B
5. 在平面直角坐标系中,函数y=-x+1与y=-(x-1)2的图象大致是( )
D
?
<
A
8 抛物线y=-(x-1)2向右平移1个单位长度可得到的抛物线的表达式为 .
9 将一条抛物线向右平移2个单位长度后得到了y=2x2的函数图象,则这条抛物线的表达式是( )
A. y=2x2+2 B. y=2x2-2
C. y=2(x-2)2 D. y=2(x+2)2
y=-(x-2)2
D
10. 如图,抛物线y=a(x+1)2的顶点为A,与y轴的负半轴交于点B,且OB=OA.
(1)求抛物线的表达式;
(2)若点C(-3,b)在该抛物线上,求S△ABC的值.
拓展提升
解:(1)由题意得,A(-1,0),B(0,-1).
将x=0,y=-1代入抛物线表达式,得a=-1.
所以抛物线的表达式为y=-(x+1)2=-x2-2x-1.
(2)如图,过点C作CD⊥x轴交x轴于点D.
将点C(-3,b)代入抛物线表达式,得b=-4,即点C(-3,-4).
S△ABC=S梯形OBCD-S△ACD-S△AOB
11. 如图,抛物线的顶点M在x轴上,抛物线与y轴交于点N,且OM=ON=4.
(1)求抛物线的函数表达式;
解:(1)因为OM=ON=4,
所以M(4,0),N(0,4).
设抛物线的函数表达式为
y=a(x-4)2,
把N(0,4)代入得16a=4,解得
所以抛物线的函数表达式为y= (x-4)2,即y= x2-2x+4.
