5.4一次函数的图象（2） 教学设计

浙教版数学八年级上5.4一次函数的图象（2）教学设计
课题
5.4一次函数的图象（2）
单元
第五章
学科
数学
年级
八年级
学习
目标
情感态度和价值观目标
感受一次函数在生活中的妙用，具备数形结合解决问题的思维，感受数学的乐趣。
能力目标
在例题探究、合作学习的过程中培养自主探究的能力
知识目标
1.利用函数图象了解一次函数的性质
2.会利用一次函数的图象和性质解决简单的实际问题
重点
一次函数的性质
难点
一次函数的应用
学法
探究法
教法
讲授法
教学过程
教学环节
教师活动
学生活动
设计意图
回顾旧知
函数的图象的画法：
列表 （2）描点（3）连线
2.函数图象与坐标轴的交点
令x=0，解出y的值即直线与y轴交点的纵坐标；
令y=0，解出x的值即直线与x轴交点的横坐标。
回忆思考
帮助学生巩固所学，并引入课
合作学习
利用函数的图象分析下列问题：对于一次函数y=2x+3，当自变量x的值增大时，函数y的值有什么变化？对于一次函数y=-2x+3呢？
函数y=2x+3中，函数值y是随着x的增大而增大
函数y=－2x+3中，函数值y随着x的增大而减小
观察图中各个一次函数的图象，你发现了什么规律？
当k>0时，y随着x的增大而增大，图像从左往右上升
当k<0时，y随着x的增大而减小，图像从左往右下降。
观察思考
通过实例让学生发现规律
做一做
1.画出函数y＝2x+5的图象，并利用图象解答问题．
（1）x取何值时，①y＞0？②y≤0？
（2）求﹣5≤y≤5的x取值范围．
做练习
及时练习，巩固所学，总结知识点
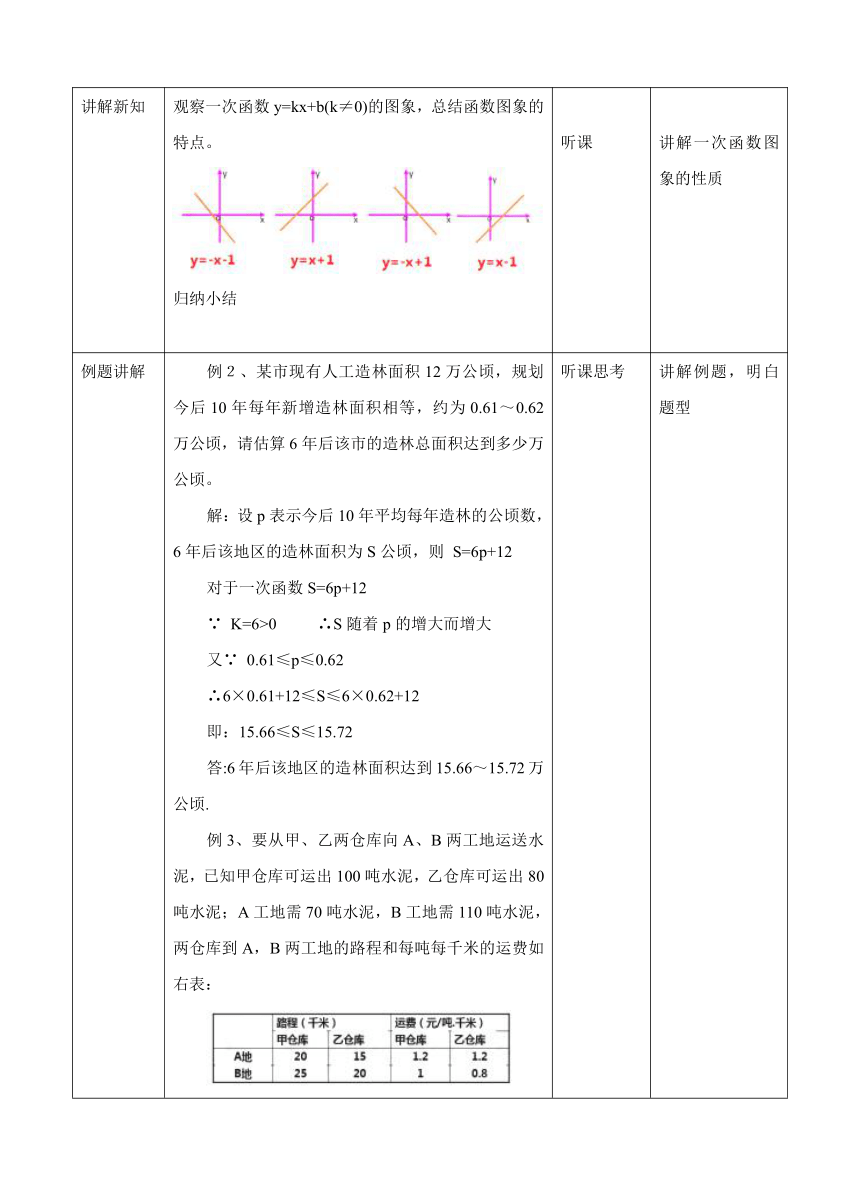
讲解新知
观察一次函数y=kx+b(k≠0)的图象，总结函数图象的特点。
归纳小结
听课
讲解一次函数图象的性质
例题讲解
例２、某市现有人工造林面积12万公顷，规划今后10年每年新增造林面积相等，约为0.61～0.62万公顷，请估算6年后该市的造林总面积达到多少万公顷。
解：设p表示今后10年平均每年造林的公顷数，6年后该地区的造林面积为S公顷，则 S=6p+12
对于一次函数S=6p+12
∵ K=6>0 ∴S随着p的增大而增大
又∵ 0.61≤p≤0.62
∴6×0.61+12≤S≤6×0.62+12
即：15.66≤S≤15.72
答:6年后该地区的造林面积达到15.66～15.72万公顷.
例3、要从甲、乙两仓库向A、B两工地运送水泥，已知甲仓库可运出100吨水泥，乙仓库可运出80吨水泥；A工地需70吨水泥，B工地需110吨水泥，两仓库到A，B两工地的路程和每吨每千米的运费如右表：
(1)设甲仓库运往A地水泥x吨,求总运费y关于x的函数解析式,并画出图象;
(2)当甲、乙两仓库各运往A，B两工地多少吨水泥时，总运费最省？最省的总运费是多少？
解：（1）各仓库运出的水泥吨数和运费如下表：
∴ y=1.2×20 x +1×25×(100- x)+1.2×15×(70- x) +0.8 ×20 ×(10+ x) = -3 x +3920
∴y关于x的函数关系式是 y=－3 x +3920
(0≤ x ≤70)
在一次函数y= －3x+3920 （0≤x≤70）中
∵k= -3 ＜ 0， ∴ y的值随x的增大而减小。
∵0 ≤x≤70，
∴当x=70时，y的值最小。
即当甲仓库向Ａ，Ｂ两工地各运送70吨和30吨水泥，乙仓库不向Ａ工地运送水泥，而只向Ｂ工地运送80吨水泥时，总运费最省，最省的部运费为
-３×70+3920=3710(元）
求最大值和最小值的方法？
（１）利用图象
（２）利用一次函数的增减性
观察右图的坐标系，你发现了什么？
当自变量的取值范围与函数值的取值范围数值相差较大时,x轴与y轴的单位长度可以取不同,并且可以采用省略画法
听课思考
讲解例题，明白题型
即时演练
有甲乙两个长方体的蓄水池，将甲池中的水以每小时6立方米的速度注入乙池，甲乙两个蓄水池中水的高度y（米）与注水时间x（小时）之间的函数图象如图所示，若要使甲乙两个蓄水池的蓄水量（指蓄水的体积）相同，则注水的时间应为___1小时______．
解：∵x=3时，甲池水量为0，
∴甲池原有水：6×3=18立方米，
3小时后乙池蓄水高度上升4-1=3米，
18÷3=6，
∴乙池中的水每升高1米，蓄水增加6立方米，
∵x=0时，乙池水高1米，
∴乙池原有水6立方米，
设x小时后甲、乙两池蓄水量（指蓄水的体积）相同，
则18-6x=6+6x，
解得x=1，
所以，注水的时间为1小时．
故答案为：1小时．
做练习
即时练习，巩固所学
达标测评
1.一次函数y=-2x-3图象上两点P1（x1，y1），P2（x2，y2）．若x1＞x2，则y1与y2的大小关系是（　　）
∵一次函数y=-2x-3中k=-2＜0，
∴此函数是减函数，
∵x1＞x2，
∴y1＜y2．
故选C．
2.若函数y=-x+b的图象不经过第一象限，则常数b的取值是（　　）
A．b＞0
B．b＜0
C．b≥0
D．b≤0
当一次函数y=-x+b的图象不经过第一象限时，
此时可能会出现如下两种情况：
①一次函数经过第二四象限，此时b=0；
②一次函数经过第二三四象限，此时b＜0；
故选D．
3.在平面直角坐标系中，已知直线y=mx+n（m＜0，n＞0），若点A（-2，y1）、（-3，y2）、C（1，y3）在直线y=mx+n上，则y1、y2、y3的大小关系为：__ y3＜y1＜y2（请用“＜”符号连接）．
∵直线y=mx+n中，m＜0，n＞0，
∴此直线经过一、二、四象限，
∴y随x的增大而减小，
∵-3＜-2＜1，
∴y3＜y1＜y2．
故答案为：y3＜y1＜y2．
4.已知一次函数y=（3-k）x-2k2+18，
（1）k为何值时，它的图象经过原点；
（2）k为何值时，它的图象经过点（0，-2）；
（3）k为何值时，它的图象与y轴的交点在x轴的上方；
（4）k为何值时，它的图象平行于直线y=-x；
（5）k为何值时，y随x的增大而减小．
（1）∵图象经过原点，
∴点（0，0）在函数图象上，代入图象解析式得：0=-2k2+18，
解得：k=±3．
又∵y=（3-k）x-2k2+18是一次函数，
∴3-k≠0，
∴k≠3．
故k=-3．
（2）∵图象经过点（0，-2），
∴点（0，-2）满足函数解析式，代入得：-2=-2k2+18，
解得：k=±．
（3）∵图象与y轴的交点在x轴的上方，
∴令x=0，得：y=-2k2+18＞0，
解得：-3＜k＜3．
（4）∵图象平行于直线y=-x，
∴两函数对应直线斜率相等即3-k=-1，
解得：k=4．
（5）∵y随x的增大而减小，
∴根据一次函数图象性质知，系数小于0，即3-k＜0，
解得：k＞3．
5.有一个附有进水管、出水管的水池，每单位时间内进出水管的进、出水量都是一定的，设从某时刻开始，4h内只进水不出水，在随后的时间内不进水只出水，得到的时间x(h)与水量y(m3)之间的关系图（如图），回答下列问题：
（1）进水管4h共进水多少？每小时进水多少？
（2）当0≤x≤4时，y与x有何关系？
（3）当x=9时，水池中的水量是多少？
（4）若4h后，只放水不进水，那么多少小时可将水池中的水放完？
解：（1）由图象知，4h共进水20m3，所以每小时进水量为5m3
（2）y是x的正比例函数，设y=kx，由于其图象过点（4，20），所以20=4k，k=5，即y=5x(0≤x≤4)　　
（3）由图象可知：当x=9时y=10，即水池中的水量为10m3
（4）由于x≥4时，图象是一条直线，所以y是x的一次函数，设y=kx+b，由图象可知，该直线过点（4，20），（9，10）
∴ 20=4k+b 解得 k=-2
10=9k+b b=28
∴y= -2x+28
令y=0，则-2x+28=0，∴x=14
14-4=10，所以4h后，只放水不进水，10h就可以把水池里的水放完。
做题
通过做对应的题目，来让学生更深刻理解本节知识
课堂小结
这节课我们学习了：
1.一次函数图象的性质
对于一次函数y=kx+b(k、b为常数，且k≠0),
当k>0时，y随着x的增大而增大；这时函数的图象从左到右上升；
当k<0时，y随着x的增大而减小；这时函数的图象从左到右下降。
2.求最大值和最小值的方法：
（１）利用图象
（２）利用一次函数的增减性
回忆总结
带领学生回忆本课所学
布置作业
课本P161页第3、 4、 5 题
做练习
课下练习提升
板书
5.4 一次函数的图象（2）
1.一次函数图象的性质：
当k>0时，y随着x的增大而增大；这时函数的图象从左到右上升；
当k<0时，y随着x的增大而减小；这时函数的图象从左到右下降。
2.应用
看黑板
帮助学生梳理本课知识点