第3章 圆的基本性质 单元测试卷(有答案)
文档属性
| 名称 | 第3章 圆的基本性质 单元测试卷(有答案) |  | |
| 格式 | zip | ||
| 文件大小 | 294.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-22 18:15:14 | ||
图片预览



文档简介
2020-2021学年浙教新版九年级上册数学《第3章
圆的基本性质》单元测试卷
一.选择题(共10小题)
1.下面说法正确的是( )
A.一条路已经修了80%千米
B.半径是2厘米的圆,它的周长和面积相等
C.某班的出勤率达到101%
D.某校的男同学人数比女同学人数多10%
2.半径为10的⊙O,圆心在直角坐标系的原点O,则点P(8,6)与⊙O的位置关系是( )
A.在⊙O上
B.在⊙O内
C.在⊙O外
D.不能确定
3.如图,在直角坐标系中,点A(0,3)、点B(4,3)、点C(0,﹣1),则△ABC外接圆的半径为( )
A.2
B.3
C.4
D.
4.如图,AB是⊙O的直径,C、D为⊙O上的点,弧AD=弧CD,若∠CAB=40°,则∠CAD=( )
A.30°
B.40°
C.50°
D.25°
5.如图,已知A、B、C、D、E是⊙O上的五个点,圆心O在AD上,∠BCD=110°,则∠AEB的度数为( )
A.70°
B.35°
C.40°
D.20°
6.下面说法正确的个数有( )
①若m>n,则ma2>nb2;
②由三条线段首尾顺次相接所组成的图形叫做三角形;
③有两个角互余的三角形一定是直角三角形;
④各边都相等的多边形是正多边形;
⑤如果一个三角形只有一条高在三角形的内部,那么这个三角形一定是钝角三角形.
A.1
个
B.2
个
C.3
个
D.4
个
7.如图,扇形OAB中,OB=3,∠AOB=100°,点C在OB上,连接AC,点O关于AC的对称点D刚好落在上,则的长是( )
A.
B.
C.
D.
8.在直角坐标系中,点O为坐标原点,点A(3,4),把线段OA绕点O顺时针旋转90°得到线段OA',则点A'的坐标为( )
A.(4,3)
B.(4,﹣3)
C.(﹣4,3)
D.(3,﹣4)
9.如图,半径为R的⊙O的弦AC=BD,且AC⊥BD于E,连结AB、AD,若AD=,则半径R的长为( )
A.1
B.
C.
D.
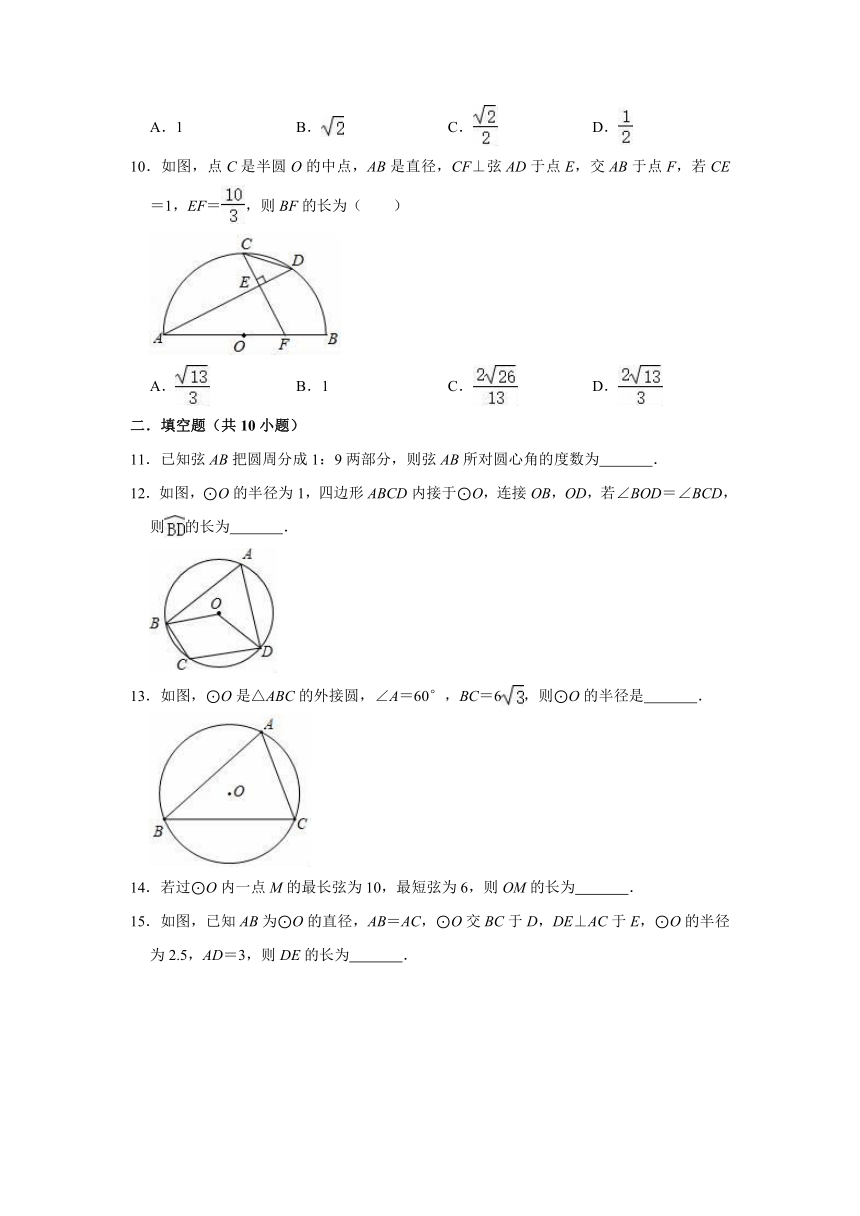
10.如图,点C是半圆O的中点,AB是直径,CF⊥弦AD于点E,交AB于点F,若CE=1,EF=,则BF的长为( )
A.
B.1
C.
D.
二.填空题(共10小题)
11.已知弦AB把圆周分成1:9两部分,则弦AB所对圆心角的度数为
.
12.如图,⊙O的半径为1,四边形ABCD内接于⊙O,连接OB,OD,若∠BOD=∠BCD,则的长为
.
13.如图,⊙O是△ABC的外接圆,∠A=60°,BC=6,则⊙O的半径是
.
14.若过⊙O内一点M的最长弦为10,最短弦为6,则OM的长为
.
15.如图,已知AB为⊙O的直径,AB=AC,⊙O交BC于D,DE⊥AC于E,⊙O的半径为2.5,AD=3,则DE的长为
.
16.在平面直角坐标系中有A,B,C三点,A(1,3),B(3,3),C(5,1).现在要画一个圆同时经过这三点,则圆心坐标为
.
17.如图,四边形ABCD内接于⊙O,AC平分∠BAD.若∠BDC=40°,则∠BCD的度数为
.
18.正六边形的边长为2,则边心距为
.
19.平面直角坐标系中,点A的坐标为(,1),以原点O为中心,将点A逆时针旋转150o得到点A′,则点A′的坐标为
.
20.已知一个扇形的圆心角是60°,面积是6π,那么这个扇形的弧长是
.
三.解答题(共7小题)
21.如图,在⊙O中.
(1)若=,∠ACB=80°,求∠BOC的度数;
(2)若⊙O的半径为13,且BC=10,求点O到BC的距离.
22.如图,已知⊙O与⊙O内一定点P,请用尺规作图法求作经过点P的最短弦AB.(保留作图痕迹,不写作法)
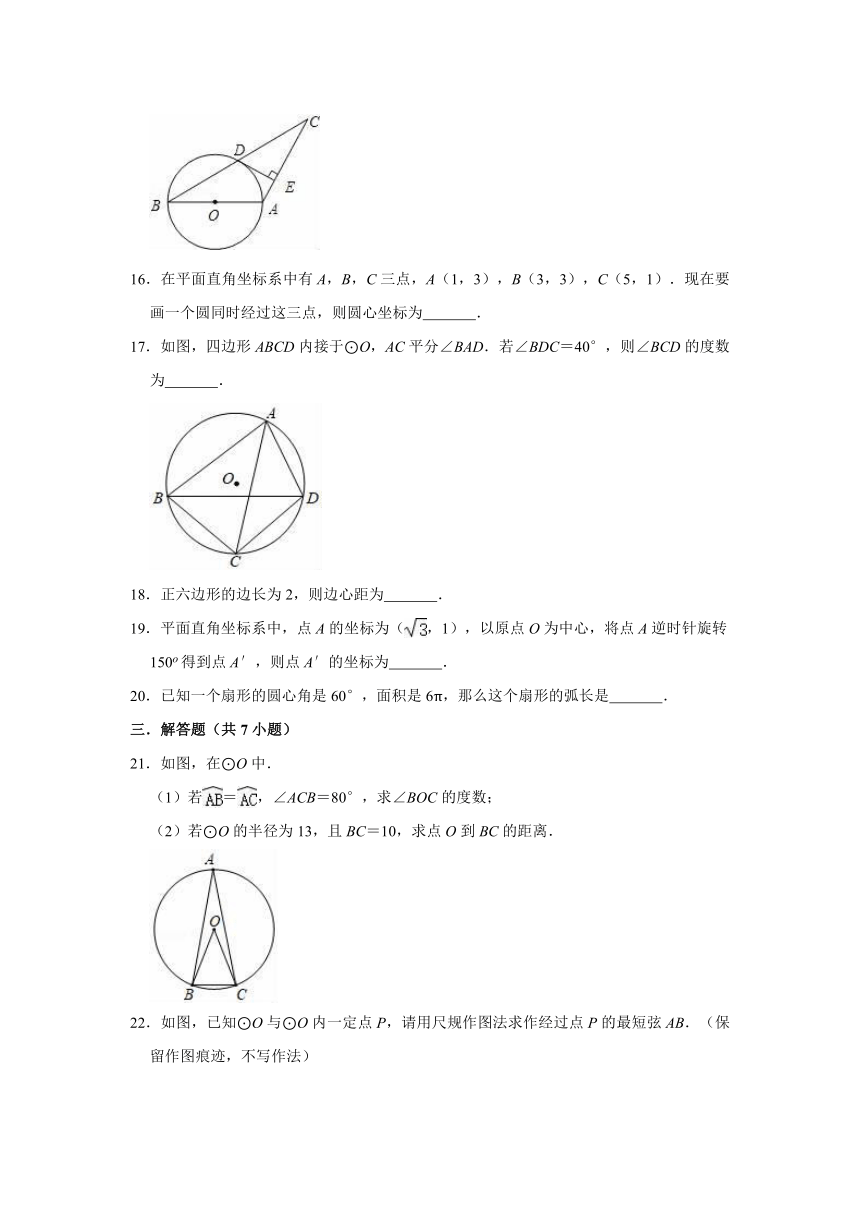
23.如图,正方形ABCD内接于⊙O,P为上一点,连接DE,AE.
(1)∠CPD=
°;
(2)若DC=4,CP=,求DP的长.
24.如图,已知AB是⊙O的直径,C,D是⊙O上的点,OC∥BD,交AD于点E,连结BC.
(1)求证:AE=ED;
(2)若AB=6,∠CBD=30°,求图中阴影部分的面积.
25.如图,Rt△ABC中,∠C=90°,AB=4,在BC上取一点D,连结AD,作△ACD的外接圆⊙O,交AB于点E.张老师要求添加条件后,编制一道题目,并解答.
(1)小明编制题目是:若AD=BD,求证:AE=BE.请你解答.
(2)在小明添加条件的基础上请你再添加一条线段的长度,编制一个计算题(不标注新的字母),并直接给出答案.(根据编出的问题层次,给不同的得分)
26.如图,图1等腰△BAC与等腰△DEC,共点于C,且∠BCA=∠ECD,连结BE、AD,若BC=AC、EC=DC.
(1)求证:BE=AD;
(2)若将等腰△DEC绕点C旋转至图2、3、4情况时,其余条件不变,BE与AD还相等吗?为什么?
(请你用图2证明你的猜想)
27.如图,四边形ABCD内接于⊙O,AB=AC,BD⊥AC,垂足为E.
(1)若∠BAC=40°,则∠ADC=
°;
(2)求证:∠BAC=2∠DAC;
(3)若AB=10,CD=5,求BC的值.
参考答案与试题解析
一.选择题(共10小题)
1.解:A:根据百分数意义,百分数表示一个数是另一个数的百分之几,不能表示具体数量,无单位,故错误;
B:圆的周长单位是厘米,面积单位是平方厘米,两者之间无法比较大小,故错误;
C:出勤率最高为100%,不可能更大了,因此选项错误;
故选:D.
2.解:∵点P(8,6),
∴OP==10,
则OP=r,
∴点P在⊙O上,
故选:A.
3.解:连接AB、BC,如图,
∵A(0,3)、B(4,3),
∴AB⊥y轴,
∴∠BAC=90°,
∴BC为△ABC外接圆的直径,
∵AC=3+1=4,AB=4,
∴BC==4,
∴△ABC外接圆的半径为2.
故选:D.
4.解:连接OD、OC,如图,
∵OA=OC,
∴∠OCA=∠OAC=40°,
∴∠AOC=180°﹣40°﹣40°=100°,
∵=,
∴∠AOD=∠COD=∠AOB=50°,
∴∠CAD=∠COD=25°.
故选:D.
5.解:如图,连接DE,
∵四边形BCDE是⊙O的内接四边形,
∴∠BCD+∠BED=180°,
∵∠BCD=110°,
∴∠BED=70°,
∵AD是⊙O的直径,
∴∠AED=90°,
∴∠AEB=∠AED﹣∠BED=90°﹣70°=20°,
故选:D.
6.解:①若m>n,则ma2>nb2,当a=0时错误;故不符合题意;
②由不在同一直线上的三条线段首尾
顺次相接所组成的图形叫做三角形,故不符合题意;
③有两个角互余的三角形一定是直角三角形,故符合题意;
④各边都相等,各角也相等的多边形是正多边形,故不符合题意.
⑤如果一个三角形只有一条高在三角形的内部,那么这个三角形是钝角三角形或直角三角形,故不符合题意;
故选:A.
7.解:连接OD,
∵点D是点O关于AC的对称点,
∴AD=OA,
∵OA=OD,
∴OA=OD=AD,
∴△OAD为等边三角形,
∴∠AOD=60°,
∴∠BOD=100°﹣60°=40°,
∴的长==π,
故选:B.
8.解:如图,由题意A(3,4),把线段OA绕点O顺时针旋转90°得到线段OA',观察图象可知A′(4,﹣3).
故选:B.
9.解:∵弦AC=BD,
∴,
∴,
∴∠ABD=∠BAC,
∴AE=BE;
连接OA,OD,
∵AC⊥BD,AE=BE,
∴∠ABE=∠BAE=45°,
∴∠AOD=2∠ABE=90°,
∵OA=OD,
∴AD=R,
∵AD=,
∴R=1,
故选:A.
10.解:如图,连接AC,BC,OC,过点B作BH⊥CF交CF的延长线于H,设OC交AD于J.
∵=,
∴AC=BC,OC⊥AB,
∵AB是直径,
∴ACB=90°,
∴∠ACJ=∠CBF=45°,
∵CF⊥AD,
∴∠ACF+∠CAJ=90°,∠ACF+∠BCF=90°,
∴∠CAJ=∠BCF,
∴△CAJ≌△BCF(ASA),
∴CJ=BF,AJ=CF=1+=,
∵OC=OB,
∴OJ=OF,设BF=CJ=x.OJ=OF=y,
∵∠AEC=∠H=90°,∠CAE=∠BCH,CA=CB,
∴△ACE≌△CBH(AAS),
∴EC=BH=1,
∵∠ECJ=∠FCO,∠CEJ=∠COF=90°,
∴△CEJ∽△COF,
∴==,
∴==,
∴EJ=,
∵BF=CJ,∠H=∠CEJ,∠CJE=∠BFH,
∴△BHF≌△CEJ(AAS),
∴FH=EJ=,
∵AE∥BH,
∴=,
∴=,
整理得,10x2+7xy﹣6y2=0,
解得x=y或x=﹣y(舍弃),
∴y=2x,
∴=,
解得x=或﹣(舍弃).
∴BF=,
故选:A.
二.填空题(共10小题)
11.解:∵弦AB把圆周分成1:9两部分,
∴弦AB所对圆心角的度数=×360°=36°.
故答案为36°.
12.解:由圆周角定理得,2∠BAD=∠BOD,
∵四边形ABCD是⊙O的内接四边形,
∴∠BCD=180°﹣∠BAD,
∴180°﹣∠BAD=2∠BAD,
解得,∠BAD=60°,
∴∠BOD=2∠BAD=120°,
∴的长==π,
故答案为:π.
13.解:作直径CD,如图,连接BD,
∵CD为直径,
∴∠CBD=90°,
∵∠D=∠A=60°,
∴BD=BC=×6=6,
∴CD=2BD=12,
∴OC=6,
即⊙O的半径是6.
故答案为6.
14.解:由已知可知,最长的弦是过M的直径AB,
最短的是垂直平分直径的弦CD,
已知AB=10,CD=8,
则OD=5,MD=4,
由勾股定理得OM=3.
故答案为:3.
15.解:∵AB为⊙O的直径,
∴∠ADB=90°,
∵AB=AC,
∴AC=5,
在Rt△ADC中,∵AC=5,AD=3,
∴CD==4,
∵×DE×AC=×AD×CD,
∴DE==.
故答案为
16.解:∵A(1,3),B(3,3),C(5,1)不在同一直线上
∴经过点A,B,C可以确定一个圆
∴该圆圆心必在线段AB的垂直平分线上
∴设圆心坐标为M(2,m)
则点M在线段BC的垂直平分线上
∴MB=MC
由勾股定理得:=
∴1+m2﹣6m+9=9+m2﹣2m+1
∴m=0
∴圆心坐标为M(2,0)
故答案为:(2,0).
17.解:∵∠BDC=40°,
∵∠BDC与∠BAC在BC的同侧,
∴∠BAC=40°,
∵AC平分∠BAD,
∴∠BAD=2∠BAC=80°,
∵四边形ABCD内接于⊙O,
∴∠BCD+∠BAD=180°;
∴∠BCD的度数为100°,
故答案为:100°.
18.解:如图所示:
连接OA、OB,作OC⊥AB于C,
则∠OCA=90°,AC=BC=AB=1,∠AOB=60°,
∴∠AOC=30°,
∴OC=AC=;
故答案为:.
19.解:如图,过点A作AE⊥x轴于E.
∵A(,1),
∴OE=,AE=1,
∴tan∠AOE==,
∴∠AOE=30°,
∴OA=OA′=2OE=2,
∵∠AOA′=150°,
∴点A′在x轴上,
∴A′(﹣2,0),
故答案为(﹣2,0).
20.解:设扇形的半径为r,
由题意,=6π,
∴r=6,
∴扇形的弧长==2π,
故答案为2π.
三.解答题(共7小题)
21.解:(1)∵=,
∴∠ABC=∠ACB=80°,
∴∠A=180°﹣80°﹣80°=20°,
∴∠BOC=2∠A=40°;
(2)作OH⊥BC于H,如图,则BH=CH=BC=5,
在Rt△OBH中,OH===12,
即点O到BC的距离为12.
22.解:如图所示:线段AB即为所求;
23.解:(1)如图,连接BD,
∵正方形ABCD内接于⊙O,P为上一点,
∴∠DBC=45°,
∵∠CPD=∠DBC,
∴∠CPD=45°.
故答案为:45;
(2)如图,作CH⊥DP于H,
∵CP=2,∠CPD=45°,
∴CH=PH=2,
∵DC=4,
∴DH===2,
∴DP=PH+DH=2+2.
24.(1)证明:∵AB是⊙O的直径,
∴∠ADB=90°,
∵OC∥BD,
∴∠AEO=∠ADB=90°,即OC⊥AD,
又∵OC为半径,
∴AE=ED,
(2)解:连接CD,OD,
∵OC∥BD,
∴∠OCB=∠CBD=30°,
∵OC=OB,
∴∠OCB=∠OBC=30°,
∴∠AOC=∠OCB+∠OBC=60°,
∵∠COD=2∠CBD=60°,
∴∠AOD=120°,
∵AB=6,
∴BD=3,AD=3,
∵OA=OB,AE=ED,
∴,
∴S阴影=S扇形AOD﹣S△AOD=﹣=3π﹣.
25.(1)证明:连结DE,
∵∠C=90°,
∴AD为直径,
∴DE⊥AB,
∵AD=BD,
∴AE=BE;
(2)答案不唯一.
①第一层次:若AC=4,求BC的长.答案:BC=8;
②第二层次:若CD=3,求BD的长.答案:BD=5;
③第三层次:若CD=3,求AC的长.
设BD=x,
∵∠B=∠B,∠C=∠DEB=90°,
∴△ABC~△DBE,
∴=,
∴=,
∴x=5,
∴AD=BD=5,
∴AC==4.
26.(1)证明:∵∠BCA=∠ECD,
∴∠BCA﹣∠ECA=∠ECD﹣∠ECA,
∴∠BCE=∠ACD,
在△BCE和△ACD中,,
∴△BCE≌△ACD(SAS),
∴BE=AD;
(2)解:图2、图3、图4中,BE=AD,理由如下:
∵∠BCA=∠ECD,
∴∠BCA﹣∠ECA=∠ECD﹣∠ECA,
∴∠BCE=∠ACD,
在△BCE和△ACD中,,
∴△BCE≌△ACD(SAS),
∴BE=AD.
27.(1)解:∵AB=AC,∠BAC=40°,
∴∠ABC=∠ACB=70°,
∵四边形ABCD是⊙O的内接四边形,
∴∠ADC=180°﹣∠BAC=110°,
故答案为:110;
(2)证明:∵BD⊥AC,
∴∠AEB=∠BEC=90°,
∴∠ACB=90°﹣∠CBD,
∵AB=AC,
∴∠ABC=∠ACB=90°﹣∠CBD,
∴∠BAC=180°﹣2∠ABC=2∠CBD,
∵∠DAC=∠CBD,
∴∠BAC=2∠DAC;
(3)解:过A作AH⊥BC于H,
∵AB=AC,
∴∠BAH=∠CAH=CAB,CH=BH,
∵∠BAC=2∠DAC,
∴∠CAG=∠CAH,
过C作CG⊥AD交AD的延长线于G,
∴∠G=∠AHC=90°,
∵AC=AC,
∴△AGC≌△AHC(AAS),
∴AG=AH,CG=CH,
∵∠CDG=∠ABC,
∴△CDG∽△ABH,
∴==,
∴=,
设BH=k,AH=2k,
∴AB==k=10,
∴k=2,
∴BC=2k=4.
圆的基本性质》单元测试卷
一.选择题(共10小题)
1.下面说法正确的是( )
A.一条路已经修了80%千米
B.半径是2厘米的圆,它的周长和面积相等
C.某班的出勤率达到101%
D.某校的男同学人数比女同学人数多10%
2.半径为10的⊙O,圆心在直角坐标系的原点O,则点P(8,6)与⊙O的位置关系是( )
A.在⊙O上
B.在⊙O内
C.在⊙O外
D.不能确定
3.如图,在直角坐标系中,点A(0,3)、点B(4,3)、点C(0,﹣1),则△ABC外接圆的半径为( )
A.2
B.3
C.4
D.
4.如图,AB是⊙O的直径,C、D为⊙O上的点,弧AD=弧CD,若∠CAB=40°,则∠CAD=( )
A.30°
B.40°
C.50°
D.25°
5.如图,已知A、B、C、D、E是⊙O上的五个点,圆心O在AD上,∠BCD=110°,则∠AEB的度数为( )
A.70°
B.35°
C.40°
D.20°
6.下面说法正确的个数有( )
①若m>n,则ma2>nb2;
②由三条线段首尾顺次相接所组成的图形叫做三角形;
③有两个角互余的三角形一定是直角三角形;
④各边都相等的多边形是正多边形;
⑤如果一个三角形只有一条高在三角形的内部,那么这个三角形一定是钝角三角形.
A.1
个
B.2
个
C.3
个
D.4
个
7.如图,扇形OAB中,OB=3,∠AOB=100°,点C在OB上,连接AC,点O关于AC的对称点D刚好落在上,则的长是( )
A.
B.
C.
D.
8.在直角坐标系中,点O为坐标原点,点A(3,4),把线段OA绕点O顺时针旋转90°得到线段OA',则点A'的坐标为( )
A.(4,3)
B.(4,﹣3)
C.(﹣4,3)
D.(3,﹣4)
9.如图,半径为R的⊙O的弦AC=BD,且AC⊥BD于E,连结AB、AD,若AD=,则半径R的长为( )
A.1
B.
C.
D.
10.如图,点C是半圆O的中点,AB是直径,CF⊥弦AD于点E,交AB于点F,若CE=1,EF=,则BF的长为( )
A.
B.1
C.
D.
二.填空题(共10小题)
11.已知弦AB把圆周分成1:9两部分,则弦AB所对圆心角的度数为
.
12.如图,⊙O的半径为1,四边形ABCD内接于⊙O,连接OB,OD,若∠BOD=∠BCD,则的长为
.
13.如图,⊙O是△ABC的外接圆,∠A=60°,BC=6,则⊙O的半径是
.
14.若过⊙O内一点M的最长弦为10,最短弦为6,则OM的长为
.
15.如图,已知AB为⊙O的直径,AB=AC,⊙O交BC于D,DE⊥AC于E,⊙O的半径为2.5,AD=3,则DE的长为
.
16.在平面直角坐标系中有A,B,C三点,A(1,3),B(3,3),C(5,1).现在要画一个圆同时经过这三点,则圆心坐标为
.
17.如图,四边形ABCD内接于⊙O,AC平分∠BAD.若∠BDC=40°,则∠BCD的度数为
.
18.正六边形的边长为2,则边心距为
.
19.平面直角坐标系中,点A的坐标为(,1),以原点O为中心,将点A逆时针旋转150o得到点A′,则点A′的坐标为
.
20.已知一个扇形的圆心角是60°,面积是6π,那么这个扇形的弧长是
.
三.解答题(共7小题)
21.如图,在⊙O中.
(1)若=,∠ACB=80°,求∠BOC的度数;
(2)若⊙O的半径为13,且BC=10,求点O到BC的距离.
22.如图,已知⊙O与⊙O内一定点P,请用尺规作图法求作经过点P的最短弦AB.(保留作图痕迹,不写作法)
23.如图,正方形ABCD内接于⊙O,P为上一点,连接DE,AE.
(1)∠CPD=
°;
(2)若DC=4,CP=,求DP的长.
24.如图,已知AB是⊙O的直径,C,D是⊙O上的点,OC∥BD,交AD于点E,连结BC.
(1)求证:AE=ED;
(2)若AB=6,∠CBD=30°,求图中阴影部分的面积.
25.如图,Rt△ABC中,∠C=90°,AB=4,在BC上取一点D,连结AD,作△ACD的外接圆⊙O,交AB于点E.张老师要求添加条件后,编制一道题目,并解答.
(1)小明编制题目是:若AD=BD,求证:AE=BE.请你解答.
(2)在小明添加条件的基础上请你再添加一条线段的长度,编制一个计算题(不标注新的字母),并直接给出答案.(根据编出的问题层次,给不同的得分)
26.如图,图1等腰△BAC与等腰△DEC,共点于C,且∠BCA=∠ECD,连结BE、AD,若BC=AC、EC=DC.
(1)求证:BE=AD;
(2)若将等腰△DEC绕点C旋转至图2、3、4情况时,其余条件不变,BE与AD还相等吗?为什么?
(请你用图2证明你的猜想)
27.如图,四边形ABCD内接于⊙O,AB=AC,BD⊥AC,垂足为E.
(1)若∠BAC=40°,则∠ADC=
°;
(2)求证:∠BAC=2∠DAC;
(3)若AB=10,CD=5,求BC的值.
参考答案与试题解析
一.选择题(共10小题)
1.解:A:根据百分数意义,百分数表示一个数是另一个数的百分之几,不能表示具体数量,无单位,故错误;
B:圆的周长单位是厘米,面积单位是平方厘米,两者之间无法比较大小,故错误;
C:出勤率最高为100%,不可能更大了,因此选项错误;
故选:D.
2.解:∵点P(8,6),
∴OP==10,
则OP=r,
∴点P在⊙O上,
故选:A.
3.解:连接AB、BC,如图,
∵A(0,3)、B(4,3),
∴AB⊥y轴,
∴∠BAC=90°,
∴BC为△ABC外接圆的直径,
∵AC=3+1=4,AB=4,
∴BC==4,
∴△ABC外接圆的半径为2.
故选:D.
4.解:连接OD、OC,如图,
∵OA=OC,
∴∠OCA=∠OAC=40°,
∴∠AOC=180°﹣40°﹣40°=100°,
∵=,
∴∠AOD=∠COD=∠AOB=50°,
∴∠CAD=∠COD=25°.
故选:D.
5.解:如图,连接DE,
∵四边形BCDE是⊙O的内接四边形,
∴∠BCD+∠BED=180°,
∵∠BCD=110°,
∴∠BED=70°,
∵AD是⊙O的直径,
∴∠AED=90°,
∴∠AEB=∠AED﹣∠BED=90°﹣70°=20°,
故选:D.
6.解:①若m>n,则ma2>nb2,当a=0时错误;故不符合题意;
②由不在同一直线上的三条线段首尾
顺次相接所组成的图形叫做三角形,故不符合题意;
③有两个角互余的三角形一定是直角三角形,故符合题意;
④各边都相等,各角也相等的多边形是正多边形,故不符合题意.
⑤如果一个三角形只有一条高在三角形的内部,那么这个三角形是钝角三角形或直角三角形,故不符合题意;
故选:A.
7.解:连接OD,
∵点D是点O关于AC的对称点,
∴AD=OA,
∵OA=OD,
∴OA=OD=AD,
∴△OAD为等边三角形,
∴∠AOD=60°,
∴∠BOD=100°﹣60°=40°,
∴的长==π,
故选:B.
8.解:如图,由题意A(3,4),把线段OA绕点O顺时针旋转90°得到线段OA',观察图象可知A′(4,﹣3).
故选:B.
9.解:∵弦AC=BD,
∴,
∴,
∴∠ABD=∠BAC,
∴AE=BE;
连接OA,OD,
∵AC⊥BD,AE=BE,
∴∠ABE=∠BAE=45°,
∴∠AOD=2∠ABE=90°,
∵OA=OD,
∴AD=R,
∵AD=,
∴R=1,
故选:A.
10.解:如图,连接AC,BC,OC,过点B作BH⊥CF交CF的延长线于H,设OC交AD于J.
∵=,
∴AC=BC,OC⊥AB,
∵AB是直径,
∴ACB=90°,
∴∠ACJ=∠CBF=45°,
∵CF⊥AD,
∴∠ACF+∠CAJ=90°,∠ACF+∠BCF=90°,
∴∠CAJ=∠BCF,
∴△CAJ≌△BCF(ASA),
∴CJ=BF,AJ=CF=1+=,
∵OC=OB,
∴OJ=OF,设BF=CJ=x.OJ=OF=y,
∵∠AEC=∠H=90°,∠CAE=∠BCH,CA=CB,
∴△ACE≌△CBH(AAS),
∴EC=BH=1,
∵∠ECJ=∠FCO,∠CEJ=∠COF=90°,
∴△CEJ∽△COF,
∴==,
∴==,
∴EJ=,
∵BF=CJ,∠H=∠CEJ,∠CJE=∠BFH,
∴△BHF≌△CEJ(AAS),
∴FH=EJ=,
∵AE∥BH,
∴=,
∴=,
整理得,10x2+7xy﹣6y2=0,
解得x=y或x=﹣y(舍弃),
∴y=2x,
∴=,
解得x=或﹣(舍弃).
∴BF=,
故选:A.
二.填空题(共10小题)
11.解:∵弦AB把圆周分成1:9两部分,
∴弦AB所对圆心角的度数=×360°=36°.
故答案为36°.
12.解:由圆周角定理得,2∠BAD=∠BOD,
∵四边形ABCD是⊙O的内接四边形,
∴∠BCD=180°﹣∠BAD,
∴180°﹣∠BAD=2∠BAD,
解得,∠BAD=60°,
∴∠BOD=2∠BAD=120°,
∴的长==π,
故答案为:π.
13.解:作直径CD,如图,连接BD,
∵CD为直径,
∴∠CBD=90°,
∵∠D=∠A=60°,
∴BD=BC=×6=6,
∴CD=2BD=12,
∴OC=6,
即⊙O的半径是6.
故答案为6.
14.解:由已知可知,最长的弦是过M的直径AB,
最短的是垂直平分直径的弦CD,
已知AB=10,CD=8,
则OD=5,MD=4,
由勾股定理得OM=3.
故答案为:3.
15.解:∵AB为⊙O的直径,
∴∠ADB=90°,
∵AB=AC,
∴AC=5,
在Rt△ADC中,∵AC=5,AD=3,
∴CD==4,
∵×DE×AC=×AD×CD,
∴DE==.
故答案为
16.解:∵A(1,3),B(3,3),C(5,1)不在同一直线上
∴经过点A,B,C可以确定一个圆
∴该圆圆心必在线段AB的垂直平分线上
∴设圆心坐标为M(2,m)
则点M在线段BC的垂直平分线上
∴MB=MC
由勾股定理得:=
∴1+m2﹣6m+9=9+m2﹣2m+1
∴m=0
∴圆心坐标为M(2,0)
故答案为:(2,0).
17.解:∵∠BDC=40°,
∵∠BDC与∠BAC在BC的同侧,
∴∠BAC=40°,
∵AC平分∠BAD,
∴∠BAD=2∠BAC=80°,
∵四边形ABCD内接于⊙O,
∴∠BCD+∠BAD=180°;
∴∠BCD的度数为100°,
故答案为:100°.
18.解:如图所示:
连接OA、OB,作OC⊥AB于C,
则∠OCA=90°,AC=BC=AB=1,∠AOB=60°,
∴∠AOC=30°,
∴OC=AC=;
故答案为:.
19.解:如图,过点A作AE⊥x轴于E.
∵A(,1),
∴OE=,AE=1,
∴tan∠AOE==,
∴∠AOE=30°,
∴OA=OA′=2OE=2,
∵∠AOA′=150°,
∴点A′在x轴上,
∴A′(﹣2,0),
故答案为(﹣2,0).
20.解:设扇形的半径为r,
由题意,=6π,
∴r=6,
∴扇形的弧长==2π,
故答案为2π.
三.解答题(共7小题)
21.解:(1)∵=,
∴∠ABC=∠ACB=80°,
∴∠A=180°﹣80°﹣80°=20°,
∴∠BOC=2∠A=40°;
(2)作OH⊥BC于H,如图,则BH=CH=BC=5,
在Rt△OBH中,OH===12,
即点O到BC的距离为12.
22.解:如图所示:线段AB即为所求;
23.解:(1)如图,连接BD,
∵正方形ABCD内接于⊙O,P为上一点,
∴∠DBC=45°,
∵∠CPD=∠DBC,
∴∠CPD=45°.
故答案为:45;
(2)如图,作CH⊥DP于H,
∵CP=2,∠CPD=45°,
∴CH=PH=2,
∵DC=4,
∴DH===2,
∴DP=PH+DH=2+2.
24.(1)证明:∵AB是⊙O的直径,
∴∠ADB=90°,
∵OC∥BD,
∴∠AEO=∠ADB=90°,即OC⊥AD,
又∵OC为半径,
∴AE=ED,
(2)解:连接CD,OD,
∵OC∥BD,
∴∠OCB=∠CBD=30°,
∵OC=OB,
∴∠OCB=∠OBC=30°,
∴∠AOC=∠OCB+∠OBC=60°,
∵∠COD=2∠CBD=60°,
∴∠AOD=120°,
∵AB=6,
∴BD=3,AD=3,
∵OA=OB,AE=ED,
∴,
∴S阴影=S扇形AOD﹣S△AOD=﹣=3π﹣.
25.(1)证明:连结DE,
∵∠C=90°,
∴AD为直径,
∴DE⊥AB,
∵AD=BD,
∴AE=BE;
(2)答案不唯一.
①第一层次:若AC=4,求BC的长.答案:BC=8;
②第二层次:若CD=3,求BD的长.答案:BD=5;
③第三层次:若CD=3,求AC的长.
设BD=x,
∵∠B=∠B,∠C=∠DEB=90°,
∴△ABC~△DBE,
∴=,
∴=,
∴x=5,
∴AD=BD=5,
∴AC==4.
26.(1)证明:∵∠BCA=∠ECD,
∴∠BCA﹣∠ECA=∠ECD﹣∠ECA,
∴∠BCE=∠ACD,
在△BCE和△ACD中,,
∴△BCE≌△ACD(SAS),
∴BE=AD;
(2)解:图2、图3、图4中,BE=AD,理由如下:
∵∠BCA=∠ECD,
∴∠BCA﹣∠ECA=∠ECD﹣∠ECA,
∴∠BCE=∠ACD,
在△BCE和△ACD中,,
∴△BCE≌△ACD(SAS),
∴BE=AD.
27.(1)解:∵AB=AC,∠BAC=40°,
∴∠ABC=∠ACB=70°,
∵四边形ABCD是⊙O的内接四边形,
∴∠ADC=180°﹣∠BAC=110°,
故答案为:110;
(2)证明:∵BD⊥AC,
∴∠AEB=∠BEC=90°,
∴∠ACB=90°﹣∠CBD,
∵AB=AC,
∴∠ABC=∠ACB=90°﹣∠CBD,
∴∠BAC=180°﹣2∠ABC=2∠CBD,
∵∠DAC=∠CBD,
∴∠BAC=2∠DAC;
(3)解:过A作AH⊥BC于H,
∵AB=AC,
∴∠BAH=∠CAH=CAB,CH=BH,
∵∠BAC=2∠DAC,
∴∠CAG=∠CAH,
过C作CG⊥AD交AD的延长线于G,
∴∠G=∠AHC=90°,
∵AC=AC,
∴△AGC≌△AHC(AAS),
∴AG=AH,CG=CH,
∵∠CDG=∠ABC,
∴△CDG∽△ABH,
∴==,
∴=,
设BH=k,AH=2k,
∴AB==k=10,
∴k=2,
∴BC=2k=4.
同课章节目录
