26.2.2 二次函数y=ax2+bx+c的图象与性质同步练习(含解析)
文档属性
| 名称 | 26.2.2 二次函数y=ax2+bx+c的图象与性质同步练习(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-23 18:45:30 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
华东师大版26.2.2
二次函数y=ax?+bx+c的图象与性质
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.抛物线的对称轴是(
)
A.直线
B.直线
C.直线
D.直线
2.抛物线的开口方向和顶点坐标分别是(
)
A.向上,
B.向下,
C.向下,
D.向上,
3.抛物线y=ax2+bx+c(a≠0)的图象如下图所示,那么(
)
A.a<0,b>0,c>0
B.a<0,b<0,c>0
C.a<0,b>0,c<0
D.a<0,b<0,c<0
4.已知二次函数y=a(x-1)2+3,当x<1时,y随x的增大而增大,则a的取值范围是( )
A.a≥0
B.a≤0
C.a>0
D.a<0
5.二次函数的图象一定不经过(
)
A.第一象限
B.第二象限
C.第三象限
D.第四象限.
6.用配方法将化成的形式为:
A.
B.
C.
D.
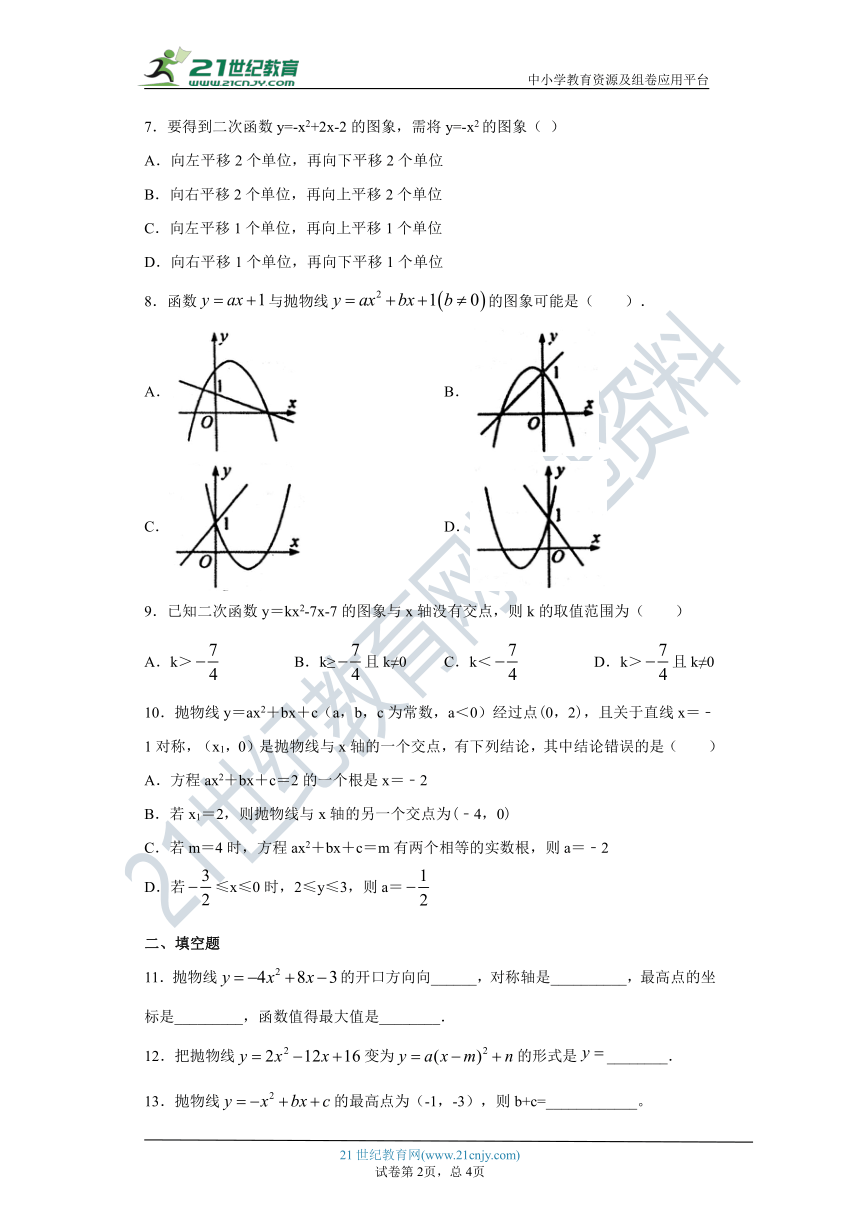
7.要得到二次函数y=-x2+2x-2的图象,需将y=-x2的图象(
)
A.向左平移2个单位,再向下平移2个单位
B.向右平移2个单位,再向上平移2个单位
C.向左平移1个单位,再向上平移1个单位
D.向右平移1个单位,再向下平移1个单位
8.函数与抛物线的图象可能是(
).
A.
B.
C.
D.
9.已知二次函数y=kx2-7x-7的图象与x轴没有交点,则k的取值范围为( )
A.k>
B.k≥且k≠0
C.k<
D.k>且k≠0
10.抛物线y=ax2+bx+c(a,b,c为常数,a<0)经过点(0,2),且关于直线x=﹣1对称,(x1,0)是抛物线与x轴的一个交点,有下列结论,其中结论错误的是(
)
A.方程ax2+bx+c=2的一个根是x=﹣2
B.若x1=2,则抛物线与x轴的另一个交点为(﹣4,0)
C.若m=4时,方程ax2+bx+c=m有两个相等的实数根,则a=﹣2
D.若≤x≤0时,2≤y≤3,则a=
二、填空题
11.抛物线的开口方向向______,对称轴是__________,最高点的坐标是_________,函数值得最大值是________.
12.把抛物线变为的形式是________.
13.抛物线的最高点为(-1,-3),则b+c=____________。
14.如图,若抛物线y=ax2+bx+c上的P(4,0),Q两点关于它的对称轴x=1对称,则Q点的坐标为________.
15.如图,二次函数y=ax2+bx+c(a>0)的图象的顶点为点D,其图象与x轴的交点A、B的横坐标分别为-1,3,与y轴负半轴交于点C.在下面五个结论中:①2a-b=0;②a+b+c>0;③c=-3a;④只有当a=时,△ABD是等腰直角三角形;⑤使△ACB为等腰三角形的a的值有4个.其中正确的结论是________(只填序号).
三、解答题
16.已知一个二次函数的图像经过、、三点.(1)求这个二次函数的解析式;(2)将这个二次函数图像平移,使顶点移到点的位置,求所得新抛物线的解析式.
已知:二次函数
(1)求出该函数图象的顶点坐标;(2)在所提供的网格中画出该函数的草图.
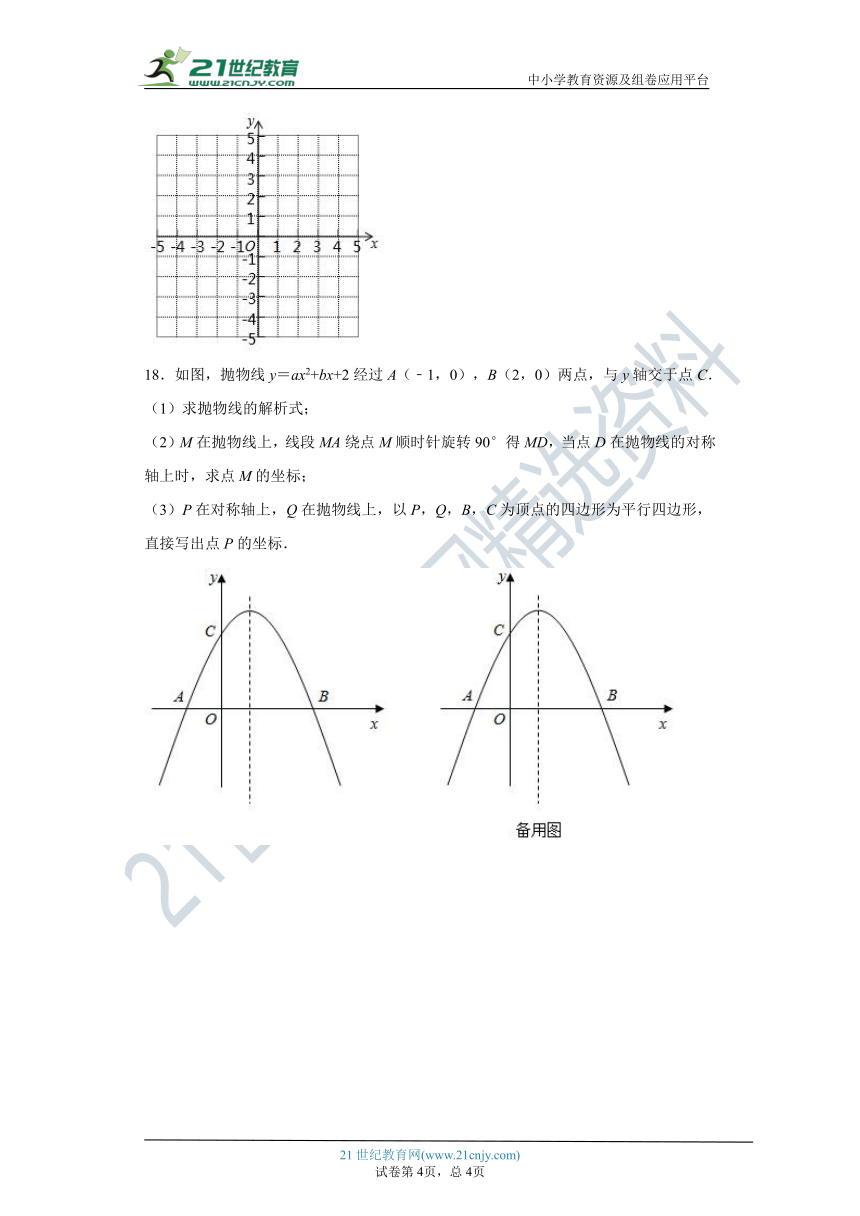
18.如图,抛物线y=ax2+bx+2经过A(﹣1,0),B(2,0)两点,与y轴交于点C.
(1)求抛物线的解析式;
(2)M在抛物线上,线段MA绕点M顺时针旋转90°得MD,当点D在抛物线的对称轴上时,求点M的坐标;
(3)P在对称轴上,Q在抛物线上,以P,Q,B,C为顶点的四边形为平行四边形,直接写出点P的坐标.
参考答案
1.C
解析:
【分析】
用对称轴公式即可得出答案.
解析:
抛物线的对称轴,
故选:C.
【点睛】
本题考查了抛物线的对称轴,熟记对称轴公式是解题的关键.
2.B
解析:
【分析】
对于抛物线y=a(x?h)2+k(a≠0),当a>0时,开口向上;当a<0时,开口向下,顶点坐标为(h,k),据此即可完成解答.
解析:
由二次函数图象的性质可知,抛物线y=?3x2+4=?3(x2-0)+4,则抛物线y=?3x2+4的开口向下,顶点坐标为(0,4).故选择B.
【点睛】
本题考查抛物线的开口方向、顶点坐标,解题的关键是掌握抛物线的开口方向、顶点坐标的求法.
3.B
【分析】
先根据图象的开口确定a的符号,利用对称轴知b的符号,与y轴的交点确定c的符号.
解析:
解:∵抛物线开口向下,
∴a<0,
∵抛物线的对称轴在y轴左侧,
∴x=-<0,
∴b<0,
∵抛物线与y轴的交点在x轴上方,
∴c>0,
故选B.
【点睛】
本题考查了二次函数图象与系数的关系:二次函数y=ax2+bx+c(a≠0),二次项系数a决定抛物线的开口方向和大小,当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;一次项系数b和二次项系数a共同决定对称轴的位置,当a与b同号时(即ab>0),对称轴在y轴左;
当a与b异号时(即ab<0),对称轴在y轴右;常数项c决定抛物线与y轴交点.抛物线与y轴交于(0,c);
4.D
解析:
:∵二次函数y=a(x-1)2+3,
∴该二次函数的对称轴为直线x=1,
又∵当x<1时,y随x的增大而增大,
∴a<0.
故选D.
【点睛】运用了二次函数的性质,解题的关键是明确在二次函数中,当a>0时,在对称轴左侧y随x的增大而减小,在对称轴右侧y随x的增大而增大;当a<0时,在对称轴左侧y随x的增大而增大,在对称轴右侧y随x的增大而减小.
5.A
解析:
∵二次函数y=ax2-2x-3(a<0)的对称轴为直线x,
∴其顶点坐标在第二或三象限,
∵当x=0时,y=-3,
∴抛物线一定经过第四象限,
∴此函数的图象一定不经过第一象限.
故选A.
6.B
解析:
试题解析:
故选B.
7.D
【分析】
根据顶点坐标的变化可以确定选项.
解析:
解:原抛物线的顶点坐标为(0,0),y=-x2+2x-2=-(x-1)2-1,所以新抛物线的顶点坐标为(1,-1),
∴将原抛物线向右平移1个单位,再向下平移1个单位可得到新抛物线.
故选D.
【点睛】
本题考查了二次函数的图象和性质,熟记平移规律和顶点坐标是解题关键.
8.C
【分析】
一次函数和二次函数与y轴交点坐标都是(0,1),然后再对a分a>0和a<0讨论即可.
解析:
解:由题意知:与抛物线与y轴的交点坐标均是(0,1),故排除选项A;
当a>0时,一次函数经过第一、二、三象限,二次函数开口向上,
故其图像有可能为选项C所示,但不可能为选项B所示;
当a<0时,一次函数经过第一、二、四象限,二次函数开口向下,不可能为为选项D所示;
故选:C.
【点睛】
本题考查了一次函数与二次函数的图像关系,熟练掌握函数的图像与系数之间的关系是解决本类题的关键.
9.C
【分析】
根据二次函数图像与x轴没有交点说明
,建立一个关于k的不等式,解不等式即可.
解析:
∵二次函数的图象与x轴无交点,
∴
即
解得
故选C.
【点睛】
本题主要考查一元二次方程根的判别式和二次函数图像与x轴交点个数的关系,掌握根的判别式是解题的关键.
10.D
【分析】
根据已知条件可将二次函数y=ax2+bx+c变形为y
=a(x+1)2﹣a+2,把x=-2代入,可对A进行判断;利用对称性可对B进行判断;依据一元二次方程根的差别式可对C进行判断;根据抛物线的图象与性质可对D进行判断.
解析:
解:由已知可得,c=2,b=2a,
∴y=ax2+2ax+2=a(x2+2x)+2=a(x+1)2﹣a+2,
A.当x=﹣2时,y=2,
∴方程ax2+bx+c=2的一个根是x=﹣2;故A正确,不符合题意;
B.若x1=2,函数的对称轴为直线x=﹣1,则抛物线与x轴的另一个交点为(﹣4,0),正确,不符合题意;
C.ax2+2ax+2=4时,△=4a2+8a=0,
∴a=0或a=﹣2,
∴a=﹣2,正确,不符合题意;
D.若﹣≤x≤0时2≤y≤3;
在﹣≤x≤0时,当x=﹣1时,y有最大值2﹣a,当x=0时,有最最小值2;
∴3=2﹣a,
∴a=﹣1,
故D.错误,符合题意;
故选:D.
【点睛】
本题考查二次函数的图象及性质;熟练掌握二次函数的图象及性质,灵活运用求根公式和函数图象的增减性是解题的关键.
11.下
直线x=1
(1,1)
1
解析:
y=-4x2+8x-3=-4(x2-2x+1)+1=-4(x-1)2+1,
∴开口方向向下,对称轴是直线x=1,最高点的坐标是(1,1),函数值的最大值是1.
故答案为下;直线x=1;(1,1);1.
点睛:函数y=ax2+bx+c=a(x+)2+,其对称轴为直线x=-,最高点坐标为(-,),函数的最值为(a>0时是最小值,a<0时是最大值).
12.
解析:
y=2x2-12x-12=2(x2-6x+9)-30=2(x-3)2-30,
则m=3,n=-30,
则mn=-90.
故答案为-90.
13.-6
解析:
由最高点为(-1,-3),
得-1=-,-3=,
解得b=-2,c=-4,
则b+c=-6.
故答案为-6.
14.(-2,0)
解析:
试题解析:因为P、Q点关于直线
对称,所以P点到直线的距离应该与Q点到直线的距离相等,P点坐标为(4,0),所以Q点的坐标为(-2,0).
故本题的答案为(-2,0).
15.③④
解析:
试题分析:先根据图象与x轴的交点A,B的横坐标分别为﹣1,3确定出AB的长及对称轴,再由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.①∵图象与x轴的交点A,B的横坐标分别为﹣1,3,∴AB=4,∴对称轴x=﹣=1,即2a+b=0.故①错误;②根据图示知,当x=1时,y<0,即a+b+c<0.故②错误;③∵A点坐标为(﹣1,0),∴a﹣b+c=0,而b=﹣2a,∴a+2a+c=0,即c=﹣3a.故③正确;④∵△ADB为等腰直角三角形.所以AD=BD=AB,设D(1,a+b+c),又b=﹣2a,c=﹣3a,故D(1,﹣4a);列方程求解得a=1/2或a=﹣1/2(舍去),∴只有a=1/2时三角形ABD为等腰直角三角形,故④正确;⑤要使△ACB为等腰三角形,则必须保证AB=BC=4或AB=AC=4或AC=BC,当AB=BC=4时,∵AO=1,△BOC为直角三角形,又∵OC的长即为|c|,∴c2=16﹣9=7,∵由抛物线与y轴的交点在y轴的负半轴上,∴c=﹣,与2a+b=0、a﹣b+c=0联立组成解方程组,解得a=;同理当AB=AC=4时,∵AO=1,△AOC为直角三角形,又∵OC的长即为|c|,∴c2=16﹣1=15,∵由抛物线与y轴的交点在y轴的负半轴上,∴c=﹣与2a+b=0、a﹣b+c=0联立组成解方程组,解得a=;同理当AC=BC时在△AOC中,AC2=1+c2,在△BOC中BC2=c2+9,∵AC=BC,∴1+c2=c2+9,此方程无解.经解方程组可知只有两个a值满足条件.故⑤错误.综上所述,正确的结论是③④.故答案是:③④.
考点:1.抛物线与x轴的交点;2.二次函数图象与系数的关系;3.等腰三角形的判定.
16.(1)
;(2)
【分析】
(1)利用待定系数法求抛物线解析式;
(2)利用顶点式写出所得新抛物线的表达式.
解析:
(1)设所求二次函数的解析式为:.
由题意,得
解得
该二次函数的解析式为.
(2)新抛物线是由二次函数的图像平移所得,
.
又顶点坐标是,
.
【点睛】
本题考查了二次函数图象与几何变换:由于抛物线平移后的形状不变,故a不变,所以求平移后的抛物线解析式通常可利用两种方法:一是求出原抛物线上任意两点平移后的坐标,利用待定系数法求出解析式;二是只考虑平移后的顶点坐标,即可求出解析式.
17.(1)
(-2,-1);(2)见解析
【分析】
(1)将二次函数化为顶点式即可得出顶点坐标;
(2)利用五点法画二次函数的图象即可.
解析:
(1)化为顶点式为
则该函数图象的顶点坐标为;
(2)先求出自变量x在处的函数值,再列出表格
当和时,
当和时,
当时,
列出表格如下:
由此画出该函数的草图如下:
【点睛】
本题考查了二次函数的顶点式、画二次函数的图象,掌握函数图象的画法是解题关键.
18.(1)y=﹣x2+x+2;(2)点M(,)或(,)或(1+,)或(1﹣,);(3)点P(,)或(,﹣)或(,).
【分析】
(1)抛物线的表达式为:y=a(x+1)(x﹣2)=a(x2﹣x﹣2),即可求解;
(2)设点M(m,﹣m2+m+2)顺时针旋转90°此时点M即为点D(﹣m2+m+2,﹣m﹣1),即可求解;
(3)分BC是平行四边形的边、BC是平行四边形的对角线两种情况,分别求解即可.
解析:
解:(1)抛物线的表达式为:y=a(x+1)(x﹣2)=a(x2﹣x﹣2),
﹣2a=2,解得:a=﹣1,
故抛物线的表达式为:y=﹣x2+x+2;
(2)设点M(m,﹣m2+m+2),
过点M作y轴的平行线HN,交过点A与x轴的平行线于点H,交x轴于点N,
∵∠DMH+∠HDM=90°,∠DMH+∠AMN=90°,
∴∠DHM=∠AMN,
又∵∠MHD=∠ANM=90°,AM=MD,
∴△MDH≌△AMN(ASA),
∴DH=MN,
即:﹣m2+m+2=|
﹣m|,
解得:m=
或1,
故点M(,)或(,)或(1+,)或(1﹣,);
(3)设点Q(m,n),n=﹣m2+m+2,点P(,s),点B、C的坐标分别为:(2,0)、(0,2),
①当BC是平行四边形的边时,
点C向右平移2个单位向上平移2个单位得到B,
同样点Q(P)向右平移2个单位向上平移2个单位得到点P(Q),
则m+2=,n﹣2=s或m﹣2=,n+2=s,
解得:s=或﹣,
故点P(,)或(,﹣);
②当BC是平行四边形的对角线时,
m+=2,n+s=2,
解得:s=,故点P(,),
综上,故点P的坐标为:(,)或(,﹣)或(,).
【点睛】
本题考查了二次函数的综合性问题,能够正确求出函数解析式以及读懂题干意思,画出具体图形,求出点的坐标是解题的关键
试卷第1页,总3页
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
试卷第1页,总3页
华东师大版26.2.2
二次函数y=ax?+bx+c的图象与性质
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.抛物线的对称轴是(
)
A.直线
B.直线
C.直线
D.直线
2.抛物线的开口方向和顶点坐标分别是(
)
A.向上,
B.向下,
C.向下,
D.向上,
3.抛物线y=ax2+bx+c(a≠0)的图象如下图所示,那么(
)
A.a<0,b>0,c>0
B.a<0,b<0,c>0
C.a<0,b>0,c<0
D.a<0,b<0,c<0
4.已知二次函数y=a(x-1)2+3,当x<1时,y随x的增大而增大,则a的取值范围是( )
A.a≥0
B.a≤0
C.a>0
D.a<0
5.二次函数的图象一定不经过(
)
A.第一象限
B.第二象限
C.第三象限
D.第四象限.
6.用配方法将化成的形式为:
A.
B.
C.
D.
7.要得到二次函数y=-x2+2x-2的图象,需将y=-x2的图象(
)
A.向左平移2个单位,再向下平移2个单位
B.向右平移2个单位,再向上平移2个单位
C.向左平移1个单位,再向上平移1个单位
D.向右平移1个单位,再向下平移1个单位
8.函数与抛物线的图象可能是(
).
A.
B.
C.
D.
9.已知二次函数y=kx2-7x-7的图象与x轴没有交点,则k的取值范围为( )
A.k>
B.k≥且k≠0
C.k<
D.k>且k≠0
10.抛物线y=ax2+bx+c(a,b,c为常数,a<0)经过点(0,2),且关于直线x=﹣1对称,(x1,0)是抛物线与x轴的一个交点,有下列结论,其中结论错误的是(
)
A.方程ax2+bx+c=2的一个根是x=﹣2
B.若x1=2,则抛物线与x轴的另一个交点为(﹣4,0)
C.若m=4时,方程ax2+bx+c=m有两个相等的实数根,则a=﹣2
D.若≤x≤0时,2≤y≤3,则a=
二、填空题
11.抛物线的开口方向向______,对称轴是__________,最高点的坐标是_________,函数值得最大值是________.
12.把抛物线变为的形式是________.
13.抛物线的最高点为(-1,-3),则b+c=____________。
14.如图,若抛物线y=ax2+bx+c上的P(4,0),Q两点关于它的对称轴x=1对称,则Q点的坐标为________.
15.如图,二次函数y=ax2+bx+c(a>0)的图象的顶点为点D,其图象与x轴的交点A、B的横坐标分别为-1,3,与y轴负半轴交于点C.在下面五个结论中:①2a-b=0;②a+b+c>0;③c=-3a;④只有当a=时,△ABD是等腰直角三角形;⑤使△ACB为等腰三角形的a的值有4个.其中正确的结论是________(只填序号).
三、解答题
16.已知一个二次函数的图像经过、、三点.(1)求这个二次函数的解析式;(2)将这个二次函数图像平移,使顶点移到点的位置,求所得新抛物线的解析式.
已知:二次函数
(1)求出该函数图象的顶点坐标;(2)在所提供的网格中画出该函数的草图.
18.如图,抛物线y=ax2+bx+2经过A(﹣1,0),B(2,0)两点,与y轴交于点C.
(1)求抛物线的解析式;
(2)M在抛物线上,线段MA绕点M顺时针旋转90°得MD,当点D在抛物线的对称轴上时,求点M的坐标;
(3)P在对称轴上,Q在抛物线上,以P,Q,B,C为顶点的四边形为平行四边形,直接写出点P的坐标.
参考答案
1.C
解析:
【分析】
用对称轴公式即可得出答案.
解析:
抛物线的对称轴,
故选:C.
【点睛】
本题考查了抛物线的对称轴,熟记对称轴公式是解题的关键.
2.B
解析:
【分析】
对于抛物线y=a(x?h)2+k(a≠0),当a>0时,开口向上;当a<0时,开口向下,顶点坐标为(h,k),据此即可完成解答.
解析:
由二次函数图象的性质可知,抛物线y=?3x2+4=?3(x2-0)+4,则抛物线y=?3x2+4的开口向下,顶点坐标为(0,4).故选择B.
【点睛】
本题考查抛物线的开口方向、顶点坐标,解题的关键是掌握抛物线的开口方向、顶点坐标的求法.
3.B
【分析】
先根据图象的开口确定a的符号,利用对称轴知b的符号,与y轴的交点确定c的符号.
解析:
解:∵抛物线开口向下,
∴a<0,
∵抛物线的对称轴在y轴左侧,
∴x=-<0,
∴b<0,
∵抛物线与y轴的交点在x轴上方,
∴c>0,
故选B.
【点睛】
本题考查了二次函数图象与系数的关系:二次函数y=ax2+bx+c(a≠0),二次项系数a决定抛物线的开口方向和大小,当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;一次项系数b和二次项系数a共同决定对称轴的位置,当a与b同号时(即ab>0),对称轴在y轴左;
当a与b异号时(即ab<0),对称轴在y轴右;常数项c决定抛物线与y轴交点.抛物线与y轴交于(0,c);
4.D
解析:
:∵二次函数y=a(x-1)2+3,
∴该二次函数的对称轴为直线x=1,
又∵当x<1时,y随x的增大而增大,
∴a<0.
故选D.
【点睛】运用了二次函数的性质,解题的关键是明确在二次函数中,当a>0时,在对称轴左侧y随x的增大而减小,在对称轴右侧y随x的增大而增大;当a<0时,在对称轴左侧y随x的增大而增大,在对称轴右侧y随x的增大而减小.
5.A
解析:
∵二次函数y=ax2-2x-3(a<0)的对称轴为直线x,
∴其顶点坐标在第二或三象限,
∵当x=0时,y=-3,
∴抛物线一定经过第四象限,
∴此函数的图象一定不经过第一象限.
故选A.
6.B
解析:
试题解析:
故选B.
7.D
【分析】
根据顶点坐标的变化可以确定选项.
解析:
解:原抛物线的顶点坐标为(0,0),y=-x2+2x-2=-(x-1)2-1,所以新抛物线的顶点坐标为(1,-1),
∴将原抛物线向右平移1个单位,再向下平移1个单位可得到新抛物线.
故选D.
【点睛】
本题考查了二次函数的图象和性质,熟记平移规律和顶点坐标是解题关键.
8.C
【分析】
一次函数和二次函数与y轴交点坐标都是(0,1),然后再对a分a>0和a<0讨论即可.
解析:
解:由题意知:与抛物线与y轴的交点坐标均是(0,1),故排除选项A;
当a>0时,一次函数经过第一、二、三象限,二次函数开口向上,
故其图像有可能为选项C所示,但不可能为选项B所示;
当a<0时,一次函数经过第一、二、四象限,二次函数开口向下,不可能为为选项D所示;
故选:C.
【点睛】
本题考查了一次函数与二次函数的图像关系,熟练掌握函数的图像与系数之间的关系是解决本类题的关键.
9.C
【分析】
根据二次函数图像与x轴没有交点说明
,建立一个关于k的不等式,解不等式即可.
解析:
∵二次函数的图象与x轴无交点,
∴
即
解得
故选C.
【点睛】
本题主要考查一元二次方程根的判别式和二次函数图像与x轴交点个数的关系,掌握根的判别式是解题的关键.
10.D
【分析】
根据已知条件可将二次函数y=ax2+bx+c变形为y
=a(x+1)2﹣a+2,把x=-2代入,可对A进行判断;利用对称性可对B进行判断;依据一元二次方程根的差别式可对C进行判断;根据抛物线的图象与性质可对D进行判断.
解析:
解:由已知可得,c=2,b=2a,
∴y=ax2+2ax+2=a(x2+2x)+2=a(x+1)2﹣a+2,
A.当x=﹣2时,y=2,
∴方程ax2+bx+c=2的一个根是x=﹣2;故A正确,不符合题意;
B.若x1=2,函数的对称轴为直线x=﹣1,则抛物线与x轴的另一个交点为(﹣4,0),正确,不符合题意;
C.ax2+2ax+2=4时,△=4a2+8a=0,
∴a=0或a=﹣2,
∴a=﹣2,正确,不符合题意;
D.若﹣≤x≤0时2≤y≤3;
在﹣≤x≤0时,当x=﹣1时,y有最大值2﹣a,当x=0时,有最最小值2;
∴3=2﹣a,
∴a=﹣1,
故D.错误,符合题意;
故选:D.
【点睛】
本题考查二次函数的图象及性质;熟练掌握二次函数的图象及性质,灵活运用求根公式和函数图象的增减性是解题的关键.
11.下
直线x=1
(1,1)
1
解析:
y=-4x2+8x-3=-4(x2-2x+1)+1=-4(x-1)2+1,
∴开口方向向下,对称轴是直线x=1,最高点的坐标是(1,1),函数值的最大值是1.
故答案为下;直线x=1;(1,1);1.
点睛:函数y=ax2+bx+c=a(x+)2+,其对称轴为直线x=-,最高点坐标为(-,),函数的最值为(a>0时是最小值,a<0时是最大值).
12.
解析:
y=2x2-12x-12=2(x2-6x+9)-30=2(x-3)2-30,
则m=3,n=-30,
则mn=-90.
故答案为-90.
13.-6
解析:
由最高点为(-1,-3),
得-1=-,-3=,
解得b=-2,c=-4,
则b+c=-6.
故答案为-6.
14.(-2,0)
解析:
试题解析:因为P、Q点关于直线
对称,所以P点到直线的距离应该与Q点到直线的距离相等,P点坐标为(4,0),所以Q点的坐标为(-2,0).
故本题的答案为(-2,0).
15.③④
解析:
试题分析:先根据图象与x轴的交点A,B的横坐标分别为﹣1,3确定出AB的长及对称轴,再由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.①∵图象与x轴的交点A,B的横坐标分别为﹣1,3,∴AB=4,∴对称轴x=﹣=1,即2a+b=0.故①错误;②根据图示知,当x=1时,y<0,即a+b+c<0.故②错误;③∵A点坐标为(﹣1,0),∴a﹣b+c=0,而b=﹣2a,∴a+2a+c=0,即c=﹣3a.故③正确;④∵△ADB为等腰直角三角形.所以AD=BD=AB,设D(1,a+b+c),又b=﹣2a,c=﹣3a,故D(1,﹣4a);列方程求解得a=1/2或a=﹣1/2(舍去),∴只有a=1/2时三角形ABD为等腰直角三角形,故④正确;⑤要使△ACB为等腰三角形,则必须保证AB=BC=4或AB=AC=4或AC=BC,当AB=BC=4时,∵AO=1,△BOC为直角三角形,又∵OC的长即为|c|,∴c2=16﹣9=7,∵由抛物线与y轴的交点在y轴的负半轴上,∴c=﹣,与2a+b=0、a﹣b+c=0联立组成解方程组,解得a=;同理当AB=AC=4时,∵AO=1,△AOC为直角三角形,又∵OC的长即为|c|,∴c2=16﹣1=15,∵由抛物线与y轴的交点在y轴的负半轴上,∴c=﹣与2a+b=0、a﹣b+c=0联立组成解方程组,解得a=;同理当AC=BC时在△AOC中,AC2=1+c2,在△BOC中BC2=c2+9,∵AC=BC,∴1+c2=c2+9,此方程无解.经解方程组可知只有两个a值满足条件.故⑤错误.综上所述,正确的结论是③④.故答案是:③④.
考点:1.抛物线与x轴的交点;2.二次函数图象与系数的关系;3.等腰三角形的判定.
16.(1)
;(2)
【分析】
(1)利用待定系数法求抛物线解析式;
(2)利用顶点式写出所得新抛物线的表达式.
解析:
(1)设所求二次函数的解析式为:.
由题意,得
解得
该二次函数的解析式为.
(2)新抛物线是由二次函数的图像平移所得,
.
又顶点坐标是,
.
【点睛】
本题考查了二次函数图象与几何变换:由于抛物线平移后的形状不变,故a不变,所以求平移后的抛物线解析式通常可利用两种方法:一是求出原抛物线上任意两点平移后的坐标,利用待定系数法求出解析式;二是只考虑平移后的顶点坐标,即可求出解析式.
17.(1)
(-2,-1);(2)见解析
【分析】
(1)将二次函数化为顶点式即可得出顶点坐标;
(2)利用五点法画二次函数的图象即可.
解析:
(1)化为顶点式为
则该函数图象的顶点坐标为;
(2)先求出自变量x在处的函数值,再列出表格
当和时,
当和时,
当时,
列出表格如下:
由此画出该函数的草图如下:
【点睛】
本题考查了二次函数的顶点式、画二次函数的图象,掌握函数图象的画法是解题关键.
18.(1)y=﹣x2+x+2;(2)点M(,)或(,)或(1+,)或(1﹣,);(3)点P(,)或(,﹣)或(,).
【分析】
(1)抛物线的表达式为:y=a(x+1)(x﹣2)=a(x2﹣x﹣2),即可求解;
(2)设点M(m,﹣m2+m+2)顺时针旋转90°此时点M即为点D(﹣m2+m+2,﹣m﹣1),即可求解;
(3)分BC是平行四边形的边、BC是平行四边形的对角线两种情况,分别求解即可.
解析:
解:(1)抛物线的表达式为:y=a(x+1)(x﹣2)=a(x2﹣x﹣2),
﹣2a=2,解得:a=﹣1,
故抛物线的表达式为:y=﹣x2+x+2;
(2)设点M(m,﹣m2+m+2),
过点M作y轴的平行线HN,交过点A与x轴的平行线于点H,交x轴于点N,
∵∠DMH+∠HDM=90°,∠DMH+∠AMN=90°,
∴∠DHM=∠AMN,
又∵∠MHD=∠ANM=90°,AM=MD,
∴△MDH≌△AMN(ASA),
∴DH=MN,
即:﹣m2+m+2=|
﹣m|,
解得:m=
或1,
故点M(,)或(,)或(1+,)或(1﹣,);
(3)设点Q(m,n),n=﹣m2+m+2,点P(,s),点B、C的坐标分别为:(2,0)、(0,2),
①当BC是平行四边形的边时,
点C向右平移2个单位向上平移2个单位得到B,
同样点Q(P)向右平移2个单位向上平移2个单位得到点P(Q),
则m+2=,n﹣2=s或m﹣2=,n+2=s,
解得:s=或﹣,
故点P(,)或(,﹣);
②当BC是平行四边形的对角线时,
m+=2,n+s=2,
解得:s=,故点P(,),
综上,故点P的坐标为:(,)或(,﹣)或(,).
【点睛】
本题考查了二次函数的综合性问题,能够正确求出函数解析式以及读懂题干意思,画出具体图形,求出点的坐标是解题的关键
试卷第1页,总3页
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
试卷第1页,总3页
