5.3 一元一次方程的应用(2)

(共15张PPT)
首先把宇宙万物的所有问题都转化为数学问题；其次，把所有的数学问题转化为代数问题；最后，把所有的代数问题转化为解方程。
笛卡尔
一个伟大的设想
东恩中学 李珊珊
运用方程解决实际问题的一般过程是:
1.审题
2.设元
3.列方程
4.解方程
5.检验
温习室
一瓶开水，可以倒满7小杯和2大杯，或者4小杯和4大杯，大杯的容量是30ml，求小杯的容量是多少
情景屋
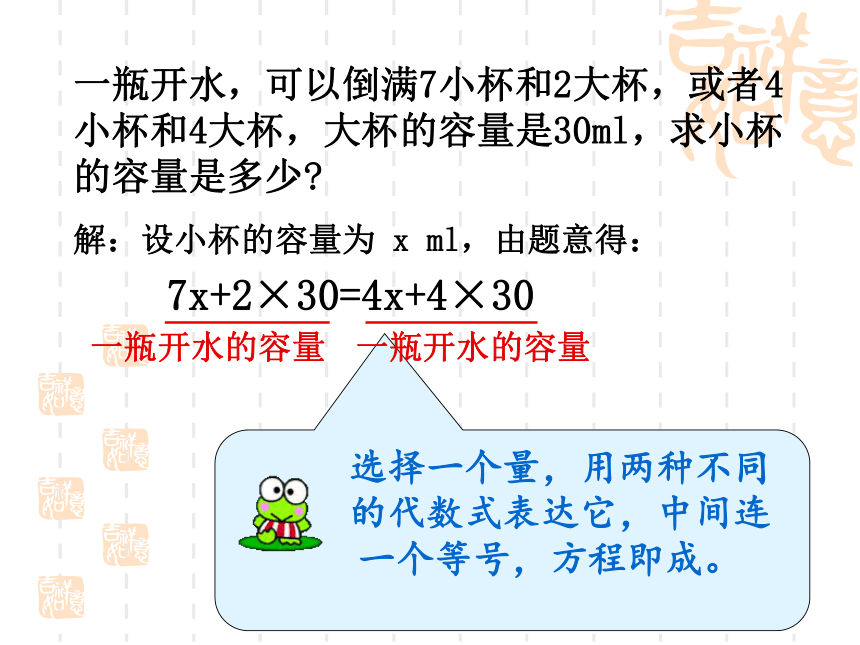
一瓶开水，可以倒满7小杯和2大杯，或者4小杯和4大杯，大杯的容量是30ml，求小杯的容量是多少
解：设小杯的容量为 x ml，由题意得：
7x+2×30=4x+4×30
选择一个量，用两种不同
的代数式表达它，中间连
一个等号，方程即成。
一瓶开水的容量
一瓶开水的容量
一瓶开水，可以倒满7小杯和2大杯，或者4小杯和4大杯，大杯的容量是30ml，求小杯的容量是多少
解：设小杯的容量为 x ml，由题意得：
7x+2×30=4x+4×30 (两种方式表示一瓶开水的容量）
7x=4x+4×30-2×30 (两种方式表示7小杯的容量）
2×30=4x+4×30-7x (两种方式表示2大杯的容量）
4x=7x+2×30-4×30 (两种方式表示4小杯的容量）
………………
(两种方式表示1小杯的容量）
1、请指出下列过程中，哪些量发生了变化，哪些量保持不变？
（2）把一小杯水倒入另一只大杯中。
解：水的底面积、高度发生了变化；水的体积和质量保持不变。
（1）用一根15cm长的铁丝围成一个三角形，然后把它改围成长方形。
解：围成的图形的面积发生了变化；铁丝的长度不变。
（3）用一块橡皮泥做成一个立方体，再把它改做成球。
解：形状改变；体积不变。
等积变形问题
例3、一纪念碑建筑的底面呈正方形，其四周铺上花岗石，形成一个宽为3米的正方形边框（如图中阴影部分），已知铺这个边框恰好用了192块边长为0.75米的正方形花岗石（接缝忽略不计）,问纪念碑建筑底面的边长是多少米
x
3
3
问题苑
解：设建筑的底面边长为x米，由题意得：
X
3
X
3
X
3
X
3
例4、初一年级组织植树活动,已知在甲处植树的有23人,在乙处植树的有17人.现调20人去支援,使在甲处植树的人数是乙处植树人数的2倍,应调往甲,乙两处各多少人
甲处 乙处
原有人数
增加人数
增加后人数
17+20-x
23+x
20-x
x
23
17
分析 设应调往甲处x人,题目中所涉及的有关数量及其关系可以用右表表示:
实践营
例4、初一年级组织植树活动,已知在甲处植树的有23人,在乙处植树的有17人.现调20人去支援,使在甲处植树的人数是乙处植树人数的2倍,应调往甲,乙两处各多少人
解：设应调往甲处x人，根据题意得：
23+x=2（17+20-x）
解得 x=17
20-17=3（人）
答：应调往甲处17人，乙处3人。
想一想：如果调往乙处的人数为x，方程应怎样列
调配问题
变式一、初二年级也在组织植树活动，原来丙处的人数比丁处的2倍少38人，若此时从丙处调10人去丁处，并调原来丁处人数的一半去丙处，这时，调整后的丙处比丁处多6人，求原丙处、丁处各有多少人？
训练场
解：设原来丁处有x人，原来丙处有（2x-38）人，根据题意得：
解得 x=32
2×32-38=26（人）
答：原来丙处有26人，丁处有32人。
变式二、学校组织植树之前先组织了初三年级120名团员先去挖土运土，另外还调来了一台挖土机，已知挖土机每天能挖土400m3，每位团员每天能挖土3m3或运土5m3，如何分配挖土和运土人数，才能使挖出的土可以及时运走？
拓展吧
解：设分配x人挖土，（120-x）人运土，根据题意得：
400+3x=5（120-x）
解得 x=25
120-25=95（人）
答：分配25人挖土，95人运土才能使挖出的土及时运走。
在等积变形的题目中，要抓住面积或体积不变的等量关系，来进行列方程，以便更好的解决实际问题。
点睛帚
在调配问题的题目中，我们一般可以通过分析实际问题, 抽象出数学问题, 然后运用数学思想方法解决问题.用列表分析数量关系是常用的方法.
选择一个量，用两种不同的代数式表达它，中间连一个等号，方程即成。
作业：
课时训练5.3（2）
作业本5.3（2）
同学们， 是金子总会发光, 相信自己是最棒的!