浙教版九年级数学上册作业本:第4章 相似三角形检测卷(含答案)
文档属性
| 名称 | 浙教版九年级数学上册作业本:第4章 相似三角形检测卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 183.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-25 00:00:00 | ||
图片预览

文档简介
1082040012065000第4章 相似三角形检测卷
一、选择题(本大题共10小题,每小题4分,共40分)
1.若x是3和6的比例中项,则x的值为( )
A.3 B.-3 C.±2 D.±3
2.在比例尺是1∶38000的南京交通游览图上,玄武湖隧道的长约为7cm,它的实际长度约为( )
A.0.266km B.2.66km C.26.6km D.266km
3.(连云港中考)如图,已知△ABC∽△DEF,AB∶DE=1∶2,则下列等式一定成立的是( )
A.= B.=
C.= D.=
第3题图
第4题图
4.如图,△ABC中,P为AB上一点,在下列四个条件中:①∠ACP=∠B;②∠APC=∠ACB;③AC2=AP×AB;④AB×CP=AP×CB,能满足△ACP与△ACB相似的条件是( )
A.①②③ B.①③④ C.②③④ D.①②④
第5题图
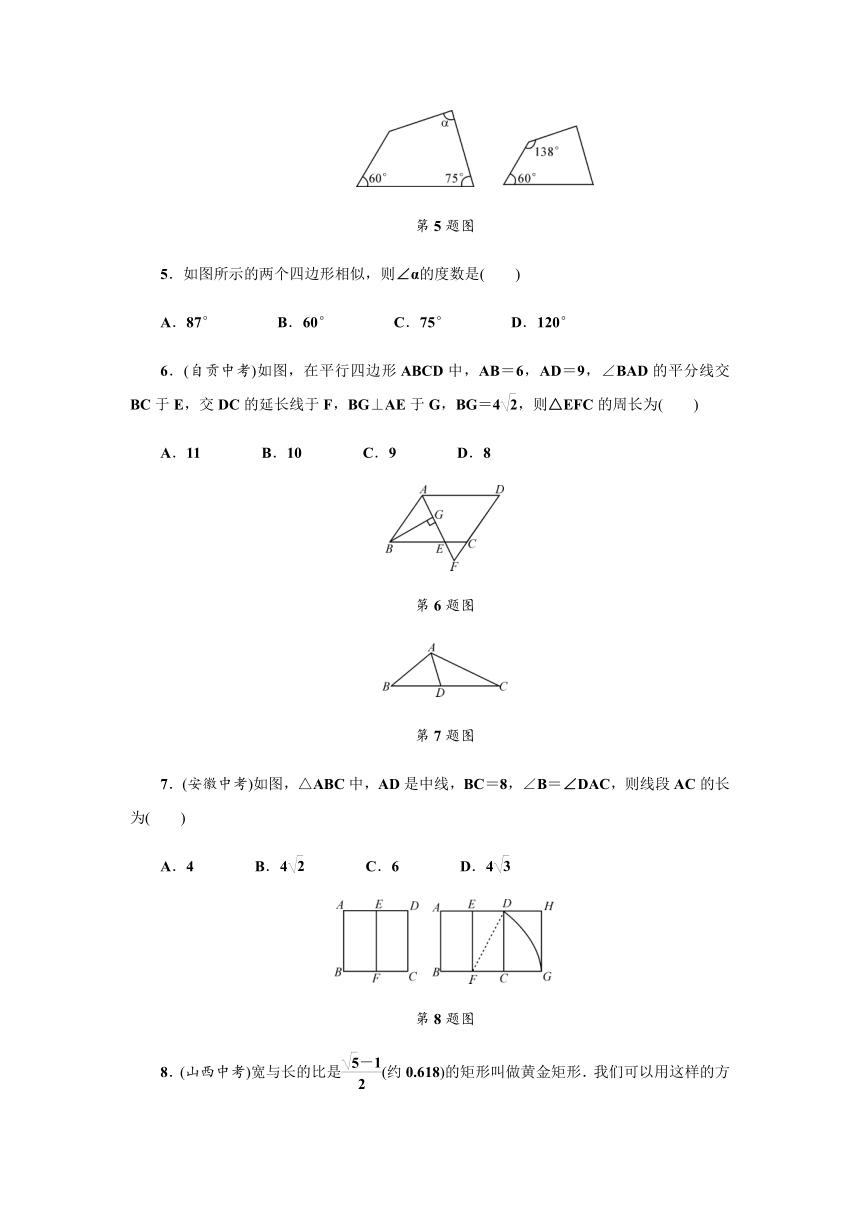
5.如图所示的两个四边形相似,则∠α的度数是( )
A.87° B.60° C.75° D.120°
6.(自贡中考)如图,在平行四边形ABCD中,AB=6,AD=9,∠BAD的平分线交BC于E,交DC的延长线于F,BG⊥AE于G,BG=4,则△EFC的周长为( )
A.11 B.10 C.9 D.8
第6题图
第7题图
7.(安徽中考)如图,△ABC中,AD是中线,BC=8,∠B=∠DAC,则线段AC的长为( )
A.4 B.4 C.6 D.4
第8题图
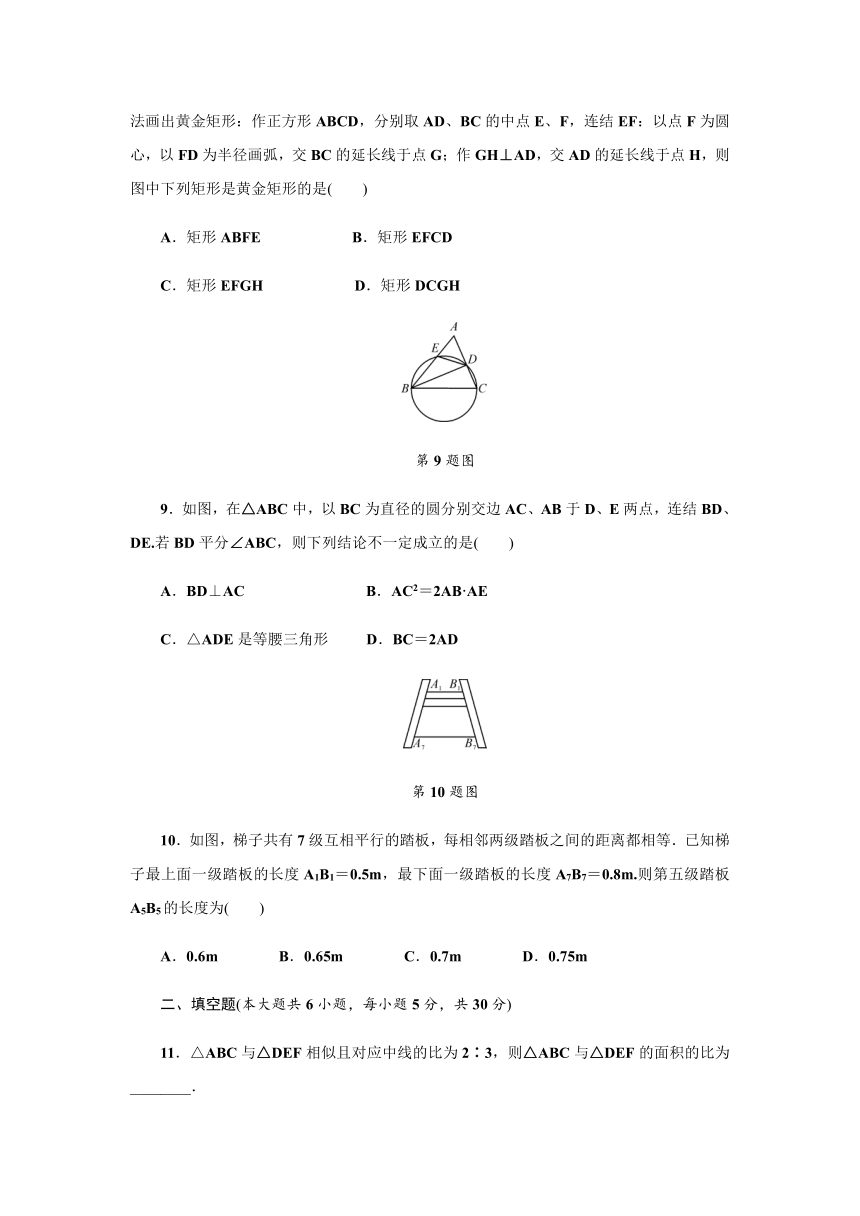
8.(山西中考)宽与长的比是(约0.618)的矩形叫做黄金矩形.我们可以用这样的方法画出黄金矩形:作正方形ABCD,分别取AD、BC的中点E、F,连结EF:以点F为圆心,以FD为半径画弧,交BC的延长线于点G;作GH⊥AD,交AD的延长线于点H,则图中下列矩形是黄金矩形的是( )
A.矩形ABFE B.矩形EFCD
C.矩形EFGH D.矩形DCGH
第9题图
9.如图,在△ABC中,以BC为直径的圆分别交边AC、AB于D、E两点,连结BD、DE.若BD平分∠ABC,则下列结论不一定成立的是( )
A.BD⊥AC B.AC2=2AB·AE
C.△ADE是等腰三角形 D.BC=2AD
第10题图
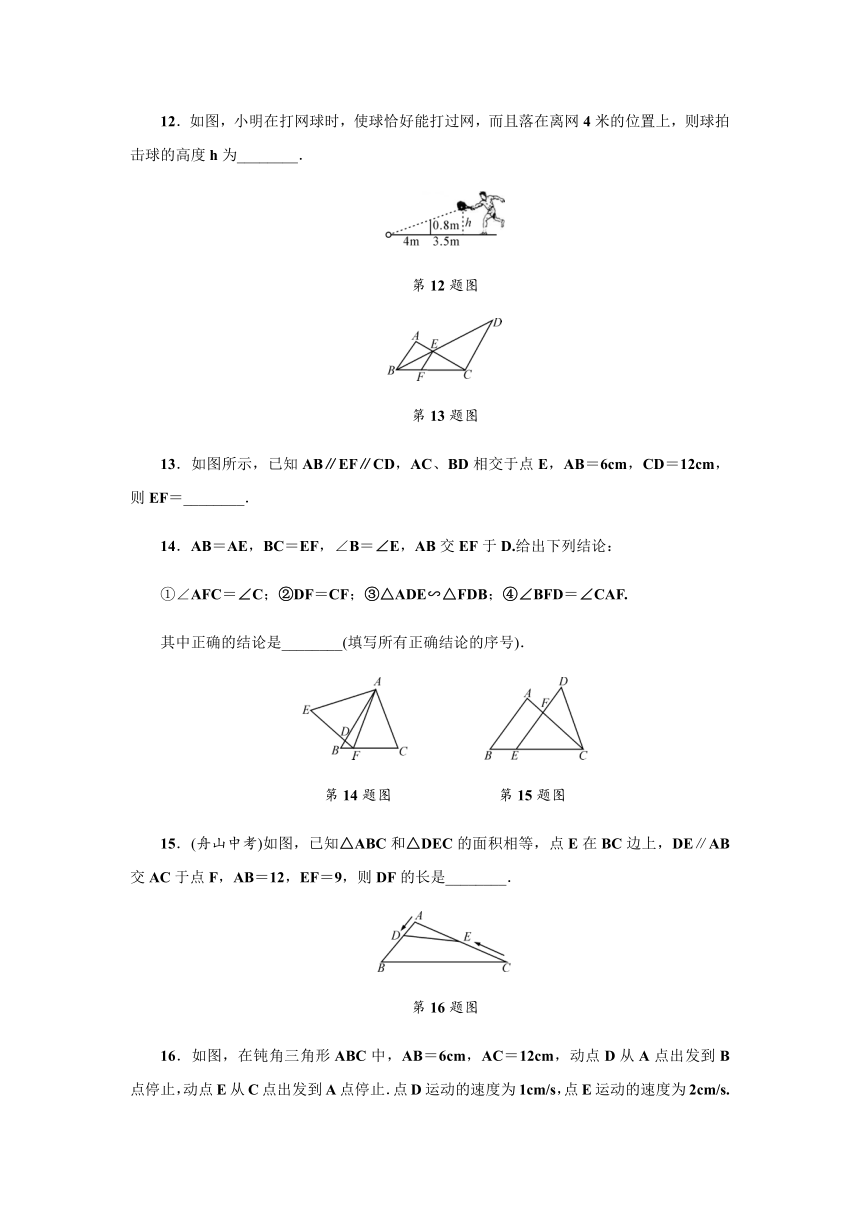
10.如图,梯子共有7级互相平行的踏板,每相邻两级踏板之间的距离都相等.已知梯子最上面一级踏板的长度A1B1=0.5m,最下面一级踏板的长度A7B7=0.8m.则第五级踏板A5B5的长度为( )
A.0.6m B.0.65m C.0.7m D.0.75m
二、填空题(本大题共6小题,每小题5分,共30分)
11.△ABC与△DEF相似且对应中线的比为2∶3,则△ABC与△DEF的面积的比为________.
12.如图,小明在打网球时,使球恰好能打过网,而且落在离网4米的位置上,则球拍击球的高度h为________.
第12题图
第13题图
13.如图所示,已知AB∥EF∥CD,AC、BD相交于点E,AB=6cm,CD=12cm,则EF=________.
14.AB=AE,BC=EF,∠B=∠E,AB交EF于D.给出下列结论:
①∠AFC=∠C;②DF=CF;③△ADE∽△FDB;④∠BFD=∠CAF.
其中正确的结论是________(填写所有正确结论的序号).
第14题图 第15题图
15.(舟山中考)如图,已知△ABC和△DEC的面积相等,点E在BC边上,DE∥AB交AC于点F,AB=12,EF=9,则DF的长是________.
第16题图
16.如图,在钝角三角形ABC中,AB=6cm,AC=12cm,动点D从A点出发到B点停止,动点E从C点出发到A点停止.点D运动的速度为1cm/s,点E运动的速度为2cm/s.如果两点同时运动,那么当以点A,D,E为顶点的三角形与△ABC相似时,运动的时间t为________s.
三、解答题(本大题共8小题,共80分)
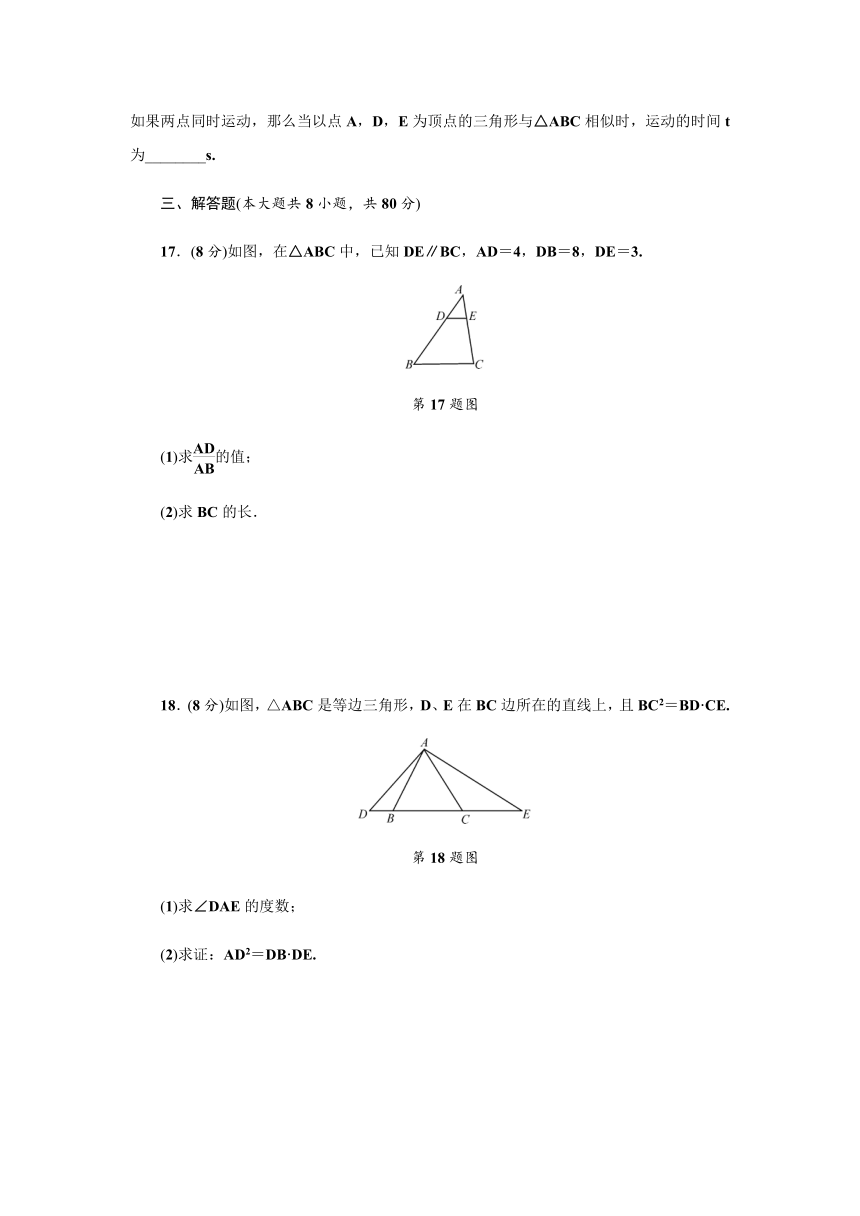
17.(8分)如图,在△ABC中,已知DE∥BC,AD=4,DB=8,DE=3.
第17题图
(1)求的值;
(2)求BC的长.
18.(8分)如图,△ABC是等边三角形,D、E在BC边所在的直线上,且BC2=BD·CE.
第18题图
(1)求∠DAE的度数;
(2)求证:AD2=DB·DE.
19.(8分)已知矩形ABCD的一条边AD=8,将矩形ABCD折叠,使得顶点B落在CD边上的P点处.如图,已知折痕与边BC交于O,连结AP、OP、OA.
(1)求证:△OCP∽△PDA;
(2)若△OCP与△PDA的面积比为1∶4,求边AB的长.
第19题图
20.(8分)(杭州中考)如图,在△ABC中,点D,E分别在边AB,AC上,∠AED=∠B,射线AG分别交线段DE,BC于点F,G,且=.
(1)求证:△ADF∽△ACG;
(2)若=,求的值.
第20题图
21.(10分)(威海中考)(1)如图1,已知∠ACB=∠DCE=90°,AC=BC=6,CD=CE,AE=3,∠CAE=45°,求AD的长;
(2)如图,已知∠ACB=∠DCE=90°,∠ABC=∠CED=∠CAE=30°,AC=3,AE=8,求AD的长.
第21题图
22.(12分)如图△ABC的三个顶点都在⊙O上,∠BAC的平分线与BC边和⊙O分别交于点D、E.
(1)指出图中相似的三角形,并说明理由;
(2)若EC=4,DE=2,求AD的长.
第22题图
23.(12分)如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连结DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC;
(2)若AB=4,AD=3,AE=3,求AF的长.
第23题图
24.(14分)函数y=-x-12的图象分别交x轴,y轴于A,C两点.
(1)在x轴上找出点B,使△ACB∽△AOC,若抛物线经过A、B、C三点,求出抛物线的解析式;
(2)在(1)的条件下,设动点P、Q分别从A、B两点同时出发,以相同的速度沿AC、BA向C、A运动,连结PQ,设AP=m,是否存在m值,使以A、P、Q为顶点的三角形与△ABC相似,若存在,求出所有的m值;若不存在,请说明理由.
第24题图
参考答案
1.D 2.B 3.D 4.A 5.A 6.D 7.B 8.D 9.D
10.C 11.4∶9 12.1.5米 13.4cm 14.①③④ 15.7 16.3或4.8 17.(1); (2)BC=9. 18.(1)∵△ABC是等边三角形,∴∠ABC=∠ACB=60°,AB=AC=BC,∴∠ABD=∠ACE,∵BC2=BD·CE,∴AB·AC=BD·CE,即=,∴△ABD∽△ECA;∴∠DAB=∠E,∴∠DAE=∠DAB+∠BAC+∠EAC=120°; (2)证明:∵∠DAE=∠ABD=120°,∠D=∠D,∴△ABD∽△EAD,∴=,∴AD2=DB·DE. 19.(1)∵四边形ABCD是矩形,∴AD=BC,DC=AB,∠DAB=∠B=∠C=∠D=90°.由折叠可得:AP=AB,PO=BO,∠PAO=∠BAO,∠APO=∠B.∴∠APO=90°.∴∠APD=90°-∠CPO=∠POC.∵∠D=∠C,∠APD=∠POC,∴△OCP∽△PDA. (2)∵△OCP与△PDA的面积比为1∶4,∴====.∴PD=2OC,PA=2OP,DA=2CP.∵AD=8,∴CP=4,BC=8.设OP=x,则OB=x,CO=8-x,在Rt△PCO中,∵∠C=90°,CP=4,OP=x,CO=8-x,∴x2=(8-x)2+42.解得:x=5.∵AB=AP=2OP=10,∴边AB的长为10. 20.(1)证明:∵∠AED=∠B,∠DAE=∠BAC,∴∠ADF=∠C,∵=,∴△ADF∽△ACG; (2)∵△ADF∽△ACG,∴=,又∵=,∴=,∴=1.
21.(1)如图1,连结BE,∵∠ACB=∠DCE=90°,∴∠ACB+∠ACE=∠DCE+∠ACE,即∠BCE=∠ACD,又∵AC=BC,DC=EC,在△ACD和△BCE中,
∴△ACD≌△BCE,∴AD=BE,∵AC=BC=6,∴AB=6,∵∠BAC=∠CAE=45°,∴∠BAE=90°,在Rt△BAE中,AB=6,AE=3,∴BE=9,∴AD=9;
第21题图
(2)如图2,连结BE,在Rt△ACB和Rt△CDE中,∠ABC=∠CED=30°,易知==,∵∠ACB=∠DCE=90°,∴∠BCE=∠ACD,∴△ACD∽△BCE,∴==,∵∠BAC=60°,∠CAE=30°,∴∠BAE=90°,又AB=6,AE=8,∴BE=10,∴AD=. 22.(1)∵AE平分∠BAC,∴∠BAE=∠CAE.又∠B与∠AEC都对应,∴∠B=∠AEC.又∠ADB=∠CDE.∴△ABD∽△AEC∽△CED; (2)∵△AEC∽△CED,∴=,∴=,解得AE=8.∴AD=AE-DE=8-2=6. 23.(1)证明:∵四边形ABCD是平行四边形,∴AD∥BC,AB∥CD,∴∠ADF=∠CED,∠B+∠C=180°,∵∠AFE+∠AFD=180°,∠AFE=∠B,∴∠AFD=∠C,∴△ADF∽△DEC; (2)∵四边形ABCD是平行四边形,∴AD∥BC,CD=AB=4,又∵AE⊥BC,∴AE⊥AD,在Rt△ADE中,DE===6,∵△ADF∽△DEC,∴=,∴=,AF=2.
第24题图
24.(1)∵y=-x-12,∴A(-16,0),C(0,-12),∵使△ACB∽△AOC,∴过C作CB⊥AC交x轴于B,设OB=n,∴=,∴n=9,∴B(9,0),过A,B,C三点的抛物线解析式为y=(x+16)(x-9); (2)存在;∵AP=BQ=m,∴=,∴m=或=,∴m=,综上可知,m=或.
一、选择题(本大题共10小题,每小题4分,共40分)
1.若x是3和6的比例中项,则x的值为( )
A.3 B.-3 C.±2 D.±3
2.在比例尺是1∶38000的南京交通游览图上,玄武湖隧道的长约为7cm,它的实际长度约为( )
A.0.266km B.2.66km C.26.6km D.266km
3.(连云港中考)如图,已知△ABC∽△DEF,AB∶DE=1∶2,则下列等式一定成立的是( )
A.= B.=
C.= D.=
第3题图
第4题图
4.如图,△ABC中,P为AB上一点,在下列四个条件中:①∠ACP=∠B;②∠APC=∠ACB;③AC2=AP×AB;④AB×CP=AP×CB,能满足△ACP与△ACB相似的条件是( )
A.①②③ B.①③④ C.②③④ D.①②④
第5题图
5.如图所示的两个四边形相似,则∠α的度数是( )
A.87° B.60° C.75° D.120°
6.(自贡中考)如图,在平行四边形ABCD中,AB=6,AD=9,∠BAD的平分线交BC于E,交DC的延长线于F,BG⊥AE于G,BG=4,则△EFC的周长为( )
A.11 B.10 C.9 D.8
第6题图
第7题图
7.(安徽中考)如图,△ABC中,AD是中线,BC=8,∠B=∠DAC,则线段AC的长为( )
A.4 B.4 C.6 D.4
第8题图
8.(山西中考)宽与长的比是(约0.618)的矩形叫做黄金矩形.我们可以用这样的方法画出黄金矩形:作正方形ABCD,分别取AD、BC的中点E、F,连结EF:以点F为圆心,以FD为半径画弧,交BC的延长线于点G;作GH⊥AD,交AD的延长线于点H,则图中下列矩形是黄金矩形的是( )
A.矩形ABFE B.矩形EFCD
C.矩形EFGH D.矩形DCGH
第9题图
9.如图,在△ABC中,以BC为直径的圆分别交边AC、AB于D、E两点,连结BD、DE.若BD平分∠ABC,则下列结论不一定成立的是( )
A.BD⊥AC B.AC2=2AB·AE
C.△ADE是等腰三角形 D.BC=2AD
第10题图
10.如图,梯子共有7级互相平行的踏板,每相邻两级踏板之间的距离都相等.已知梯子最上面一级踏板的长度A1B1=0.5m,最下面一级踏板的长度A7B7=0.8m.则第五级踏板A5B5的长度为( )
A.0.6m B.0.65m C.0.7m D.0.75m
二、填空题(本大题共6小题,每小题5分,共30分)
11.△ABC与△DEF相似且对应中线的比为2∶3,则△ABC与△DEF的面积的比为________.
12.如图,小明在打网球时,使球恰好能打过网,而且落在离网4米的位置上,则球拍击球的高度h为________.
第12题图
第13题图
13.如图所示,已知AB∥EF∥CD,AC、BD相交于点E,AB=6cm,CD=12cm,则EF=________.
14.AB=AE,BC=EF,∠B=∠E,AB交EF于D.给出下列结论:
①∠AFC=∠C;②DF=CF;③△ADE∽△FDB;④∠BFD=∠CAF.
其中正确的结论是________(填写所有正确结论的序号).
第14题图 第15题图
15.(舟山中考)如图,已知△ABC和△DEC的面积相等,点E在BC边上,DE∥AB交AC于点F,AB=12,EF=9,则DF的长是________.
第16题图
16.如图,在钝角三角形ABC中,AB=6cm,AC=12cm,动点D从A点出发到B点停止,动点E从C点出发到A点停止.点D运动的速度为1cm/s,点E运动的速度为2cm/s.如果两点同时运动,那么当以点A,D,E为顶点的三角形与△ABC相似时,运动的时间t为________s.
三、解答题(本大题共8小题,共80分)
17.(8分)如图,在△ABC中,已知DE∥BC,AD=4,DB=8,DE=3.
第17题图
(1)求的值;
(2)求BC的长.
18.(8分)如图,△ABC是等边三角形,D、E在BC边所在的直线上,且BC2=BD·CE.
第18题图
(1)求∠DAE的度数;
(2)求证:AD2=DB·DE.
19.(8分)已知矩形ABCD的一条边AD=8,将矩形ABCD折叠,使得顶点B落在CD边上的P点处.如图,已知折痕与边BC交于O,连结AP、OP、OA.
(1)求证:△OCP∽△PDA;
(2)若△OCP与△PDA的面积比为1∶4,求边AB的长.
第19题图
20.(8分)(杭州中考)如图,在△ABC中,点D,E分别在边AB,AC上,∠AED=∠B,射线AG分别交线段DE,BC于点F,G,且=.
(1)求证:△ADF∽△ACG;
(2)若=,求的值.
第20题图
21.(10分)(威海中考)(1)如图1,已知∠ACB=∠DCE=90°,AC=BC=6,CD=CE,AE=3,∠CAE=45°,求AD的长;
(2)如图,已知∠ACB=∠DCE=90°,∠ABC=∠CED=∠CAE=30°,AC=3,AE=8,求AD的长.
第21题图
22.(12分)如图△ABC的三个顶点都在⊙O上,∠BAC的平分线与BC边和⊙O分别交于点D、E.
(1)指出图中相似的三角形,并说明理由;
(2)若EC=4,DE=2,求AD的长.
第22题图
23.(12分)如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连结DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC;
(2)若AB=4,AD=3,AE=3,求AF的长.
第23题图
24.(14分)函数y=-x-12的图象分别交x轴,y轴于A,C两点.
(1)在x轴上找出点B,使△ACB∽△AOC,若抛物线经过A、B、C三点,求出抛物线的解析式;
(2)在(1)的条件下,设动点P、Q分别从A、B两点同时出发,以相同的速度沿AC、BA向C、A运动,连结PQ,设AP=m,是否存在m值,使以A、P、Q为顶点的三角形与△ABC相似,若存在,求出所有的m值;若不存在,请说明理由.
第24题图
参考答案
1.D 2.B 3.D 4.A 5.A 6.D 7.B 8.D 9.D
10.C 11.4∶9 12.1.5米 13.4cm 14.①③④ 15.7 16.3或4.8 17.(1); (2)BC=9. 18.(1)∵△ABC是等边三角形,∴∠ABC=∠ACB=60°,AB=AC=BC,∴∠ABD=∠ACE,∵BC2=BD·CE,∴AB·AC=BD·CE,即=,∴△ABD∽△ECA;∴∠DAB=∠E,∴∠DAE=∠DAB+∠BAC+∠EAC=120°; (2)证明:∵∠DAE=∠ABD=120°,∠D=∠D,∴△ABD∽△EAD,∴=,∴AD2=DB·DE. 19.(1)∵四边形ABCD是矩形,∴AD=BC,DC=AB,∠DAB=∠B=∠C=∠D=90°.由折叠可得:AP=AB,PO=BO,∠PAO=∠BAO,∠APO=∠B.∴∠APO=90°.∴∠APD=90°-∠CPO=∠POC.∵∠D=∠C,∠APD=∠POC,∴△OCP∽△PDA. (2)∵△OCP与△PDA的面积比为1∶4,∴====.∴PD=2OC,PA=2OP,DA=2CP.∵AD=8,∴CP=4,BC=8.设OP=x,则OB=x,CO=8-x,在Rt△PCO中,∵∠C=90°,CP=4,OP=x,CO=8-x,∴x2=(8-x)2+42.解得:x=5.∵AB=AP=2OP=10,∴边AB的长为10. 20.(1)证明:∵∠AED=∠B,∠DAE=∠BAC,∴∠ADF=∠C,∵=,∴△ADF∽△ACG; (2)∵△ADF∽△ACG,∴=,又∵=,∴=,∴=1.
21.(1)如图1,连结BE,∵∠ACB=∠DCE=90°,∴∠ACB+∠ACE=∠DCE+∠ACE,即∠BCE=∠ACD,又∵AC=BC,DC=EC,在△ACD和△BCE中,
∴△ACD≌△BCE,∴AD=BE,∵AC=BC=6,∴AB=6,∵∠BAC=∠CAE=45°,∴∠BAE=90°,在Rt△BAE中,AB=6,AE=3,∴BE=9,∴AD=9;
第21题图
(2)如图2,连结BE,在Rt△ACB和Rt△CDE中,∠ABC=∠CED=30°,易知==,∵∠ACB=∠DCE=90°,∴∠BCE=∠ACD,∴△ACD∽△BCE,∴==,∵∠BAC=60°,∠CAE=30°,∴∠BAE=90°,又AB=6,AE=8,∴BE=10,∴AD=. 22.(1)∵AE平分∠BAC,∴∠BAE=∠CAE.又∠B与∠AEC都对应,∴∠B=∠AEC.又∠ADB=∠CDE.∴△ABD∽△AEC∽△CED; (2)∵△AEC∽△CED,∴=,∴=,解得AE=8.∴AD=AE-DE=8-2=6. 23.(1)证明:∵四边形ABCD是平行四边形,∴AD∥BC,AB∥CD,∴∠ADF=∠CED,∠B+∠C=180°,∵∠AFE+∠AFD=180°,∠AFE=∠B,∴∠AFD=∠C,∴△ADF∽△DEC; (2)∵四边形ABCD是平行四边形,∴AD∥BC,CD=AB=4,又∵AE⊥BC,∴AE⊥AD,在Rt△ADE中,DE===6,∵△ADF∽△DEC,∴=,∴=,AF=2.
第24题图
24.(1)∵y=-x-12,∴A(-16,0),C(0,-12),∵使△ACB∽△AOC,∴过C作CB⊥AC交x轴于B,设OB=n,∴=,∴n=9,∴B(9,0),过A,B,C三点的抛物线解析式为y=(x+16)(x-9); (2)存在;∵AP=BQ=m,∴=,∴m=或=,∴m=,综上可知,m=或.
同课章节目录
