浙教版八上第5章 一次函数实际运用综合专项训练(含解析)
文档属性
| 名称 | 浙教版八上第5章 一次函数实际运用综合专项训练(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-26 20:20:24 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
一次函数实际运用综合专项训练
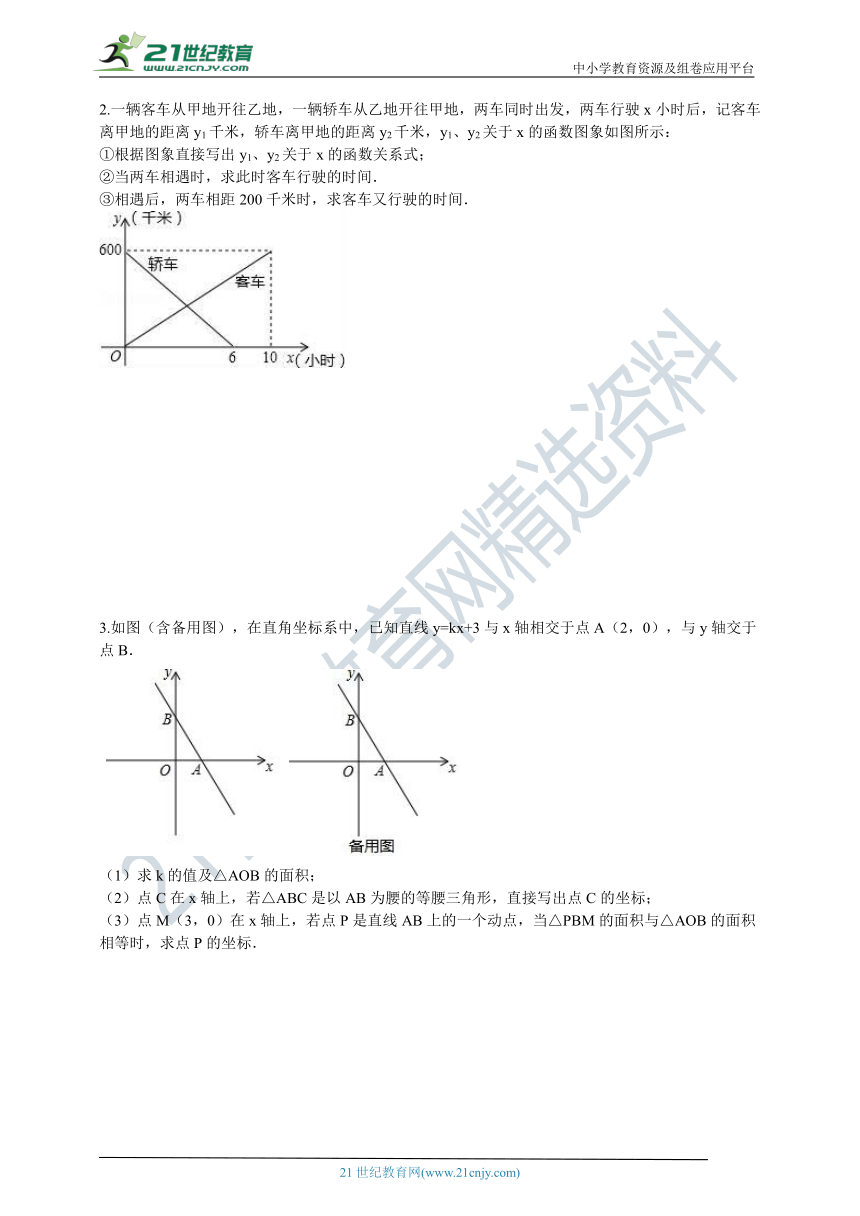
1.在“看图说故事”活动中,某学习小组结合图象设计了一个问题情境.
已知小亮所在学校的宿舍、食堂、图书馆依次在同一条直线上,食堂离宿舍
,图书馆离宿舍
.周末,小亮从宿舍出发,匀速走了
到食堂;在食堂停留
吃早餐后,匀速走了
到图书馆;在图书馆停留
借书后,匀速走了
返回宿舍,给出的图象反映了这个过程中小亮离宿舍的距离
与离开宿舍的时间
之间的对应关系.
请根据相关信息,解答下列问题:
(1)填表:
离开宿舍的时间/
2
5
20
23
30
离宿舍的距离/
0.2
________
0.7
________
________
(2)填空:
①食堂到图书馆的距离为________
.
②小亮从食堂到图书馆的速度为________
.
③小亮从图书馆返回宿舍的速度为________
.
④当小亮离宿舍的距离为
时,他离开宿舍的时间为________
.
(3)当
时,请直接写出y关于x的函数解析式.
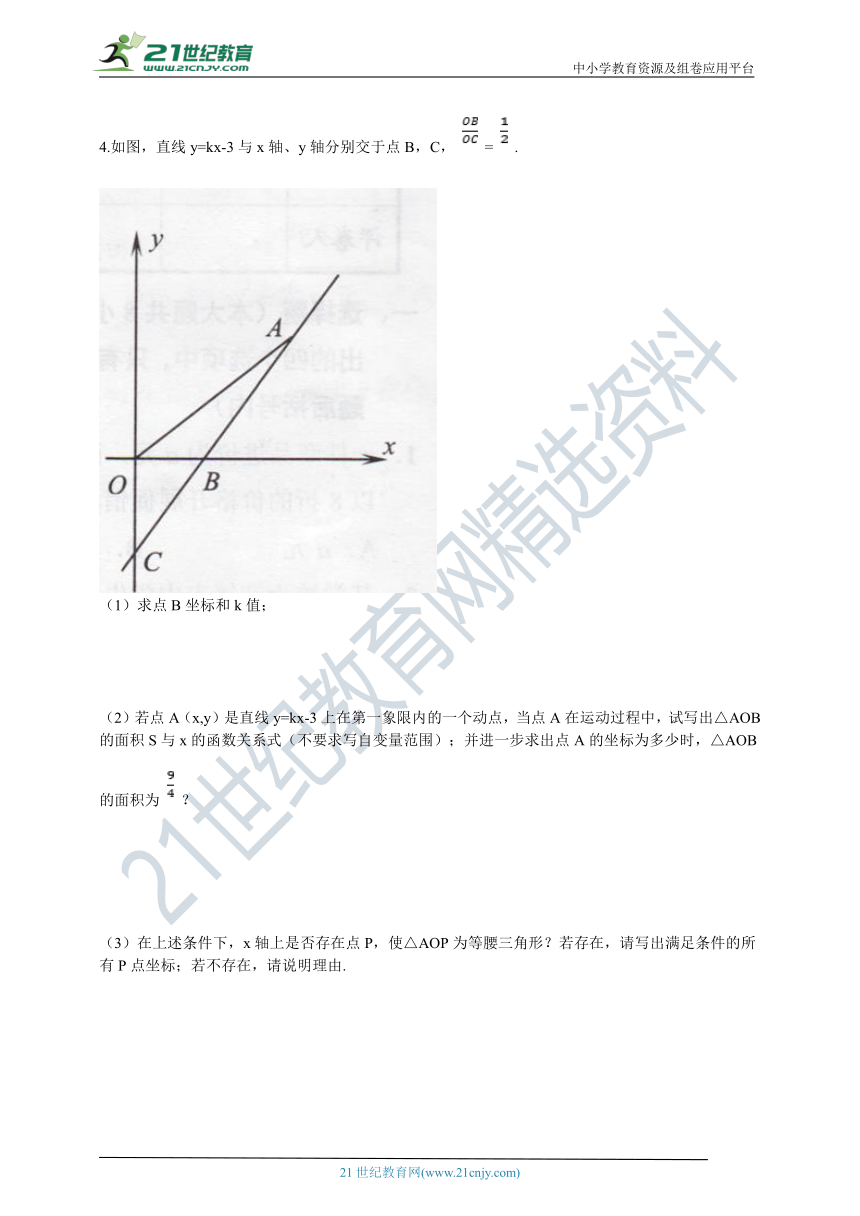
2.一辆客车从甲地开往乙地,一辆轿车从乙地开往甲地,两车同时出发,两车行驶x小时后,记客车离甲地的距离y1千米,轿车离甲地的距离y2千米,y1、y2关于x的函数图象如图所示:
①根据图象直接写出y1、y2关于x的函数关系式;
②当两车相遇时,求此时客车行驶的时间.
③相遇后,两车相距200千米时,求客车又行驶的时间.
3.如图(含备用图),在直角坐标系中,已知直线y=kx+3与x轴相交于点A(2,0),与y轴交于点B.
(1)求k的值及△AOB的面积;
(2)点C在x轴上,若△ABC是以AB为腰的等腰三角形,直接写出点C的坐标;
(3)点M(3,0)在x轴上,若点P是直线AB上的一个动点,当△PBM的面积与△AOB的面积相等时,求点P的坐标.
4.如图,直线y=kx-3与x轴、y轴分别交于点B,C,
=
.
(1)求点B坐标和k值;
(2)若点A(x,y)是直线y=kx-3上在第一象限内的一个动点,当点A在运动过程中,试写出△AOB的面积S与x的函数关系式(不要求写自变量范围);并进一步求出点A的坐标为多少时,△AOB的面积为
?
(3)在上述条件下,x轴上是否存在点P,使△AOP为等腰三角形?若存在,请写出满足条件的所有P点坐标;若不存在,请说明理由.
5.我市为创建“国家级森林城市”,政府决定对江边一处废弃荒地进行绿化,要求栽植甲、乙两种不同的树苗共6000棵,且甲种树苗不得多于乙种树苗.某承包商以26万元的报价中标承包了这项工程.根据调查及相关资料表明:移栽一棵树苗的平均费用为8元,甲、乙两种树苗的购买价及成活率如表:
品种
购买价(元/棵)
成活率
甲
20
90%
乙
32
95%
设购买甲种树苗x棵,承包商获得的利润为y元.请根据以上信息解答下列问题:
(1)设y与x之间的函数关系式,并写出自变量x的取值范围;
(2)承包商要获得不低于中标价16%的利润,应如何选购树苗?
(3)政府与承包商的合同要求,栽植这批树苗的成活率必须不低于93%,否则承包商出资补栽;若成货率达到94%以上(含94%),则政府另给予工程款总额6%的奖励,该承包商应如何选购树苗才能获得最大利润?最大利润是多少?
6.如图,在平面直角坐标系xOy中,直线y=2x+2与y轴交于点A,与x轴交于点B.直线l⊥x轴负半轴于点C,点D是直线l上一点且位于x轴上方.已知CO=CD=4.
(1)求经过A,D两点的直线的函数关系式和点B的坐标;
(2)在直线l上是否存在点P使得△BDP为等腰三角形,若存在,直接写出P点坐标,若不存在,请说明理由.
7.如图,直线y=
x+6与x轴、y轴分别相交于点E、F,点A的坐标为(-6,0),P(x,y)是直线y=
x+6上一个动点.
(1)在点P运动过程中,试写出△OPA的面积s与x的函数关系式;
(2)当P运动到什么位置,△OPA的面积为
,求出此时点P的坐标;
(3)过P作EF的垂线分别交x轴、y轴于C、D.是否存在这样的点P,使△COD≌△FOE?若存在,直接写出此时点P的坐标(不要求写解答过程);若不存在,请说明理由.
8.某天早晨,张强从家跑步去体育锻炼,同时妈妈从体育场晨练结束回家,途中两人相遇,张强跑到体育场后发现要下雨,立即按原路返回,遇到妈妈后两人一起回到家(张强和妈妈始终在同一条笔直的公路上行走).如图是两人离家的距离y(米)与张强出发的时间x(分)之间的函数图象,根据图象信息解答下列问题:
(1)求张强返回时的速度;
(2)妈妈比按原速返回提前多少分钟到家?
(3)请直接写出张强与妈妈何时相距1000米?
9.如图,在平面直角坐标系xOy中,一次函数y=k1x+b的图象与x轴交于点A(-3,0),与y轴交于点B,且与正比例函数y=kx的图象交点为C(3,4).
(1)求正比例函数与一次函数的关系式;
(2)若点D在第二象限,△DAB是以AB为直角边的等腰直角三角形,请求出点D的坐标;
(3)在x轴上是否存在一点E使△BCE周长最小,若存在,求出点E的坐标
在x轴上求一点P使△POC为等腰三角形,请直接写出所有符合条件的点P的坐标.
10.甲、乙两人利用不同的交通工具,沿同一路线分别从A、B两地同时出发匀速前往C地(B在A、C两地的途中).设甲、乙两车距A地的路程分别为y甲、y乙(千米),行驶的时间为x(小时),y甲、y乙与x之间的函数图象如图所示.
(1)直接写出y甲、y乙与x之间的函数表达式;
(2)如图,过点(1,0)作x轴的垂线,分别交y甲、y乙的图象于点M,N.求线段MN的长,并解释线段MN的实际意义;
(3)在乙行驶的过程中,当甲、乙两人距A地的路程差小于30千米时,求x的取值范围.
11.如图,Rt△AOB?在平面直角坐标系中,点O与坐标原点重合,点A在x轴上,点B在y轴上,
,将△AOB沿直线BE折叠,使得OB边落在AB上,点O与点D重合.
(1)求直线BE的解析式;
(2)求点D的坐标;
(3)x轴上是否存在点P,使△PAD为等腰三角形?若存在,请直接写出点P的坐标,若不存在,请说明理由。
12.小李和小陆从
A
地出发,骑自行车沿同一条路行驶到
B
地,他们离出发地的距离s和行驶时间t之间的关系的图象如图,根据图象回答下列问题:
(1)小李在途中逗留的时间为________h,小陆从
A
地到
B
地的速度是________km/h.
(2)当小李和小陆相遇时,他们离
B
地的路程是________千米;
(3)写出小李在逗留之前离
A
地的路程s和行驶时间t之间的函数关系式为________
13.在一条笔直的公路上有A、B两地.甲、乙两人同时出发,甲骑电动车从A地到B地,中途出现故障后停车维修,修好车后以原速继续行驶到B地;乙骑摩托车从B地到A地,到达A地后立即按原原速返回,结果两人同时到B地.如图是甲、乙两人与B地的距离y(km)与乙行驶时间x(h)之间的函数图象。
(1)A、B两地间的距离为________km;
(2)求乙与B地的距离y(km)与乙行驶时间x(h)之间的函数关系式;
(3)求甲、乙第一次相遇的时间;
(4)若两人之间的距离不超过10km时,能够用无线对讲机保持联系,请求出乙在行进中能用无线对讲机与甲保持联系的x取值范围。
14.小明某天上午9时骑自行车离开家,15时回家,他有意描绘了离家的距离与时间的变化情况(如图所示)
(1)图象表示了哪两个变量的关系?哪个是自变量?哪个是因变量?
(2)10时和13时,他分别离家多远?
(3)他到达离家最远的地方是什么时间?离家多远?
(4)11时到12时他行驶了多少千米?
(5)他可能在哪段时间内休息,并吃午餐?
(6)他由离家最远的地方返回时的平均速度是多少?
15.已知y=(m+1)x2-|m|+n+4
(1)当m、n取何值时,y是x的一次函数?
(2)当m、n取何值时,y是x的正比例函数?
16.“低碳环保,绿色出行”的理念得到广大群众的接受,越来越多的人再次选择自行车作为出行工具,小军和爸爸同时从家骑自行车去图书馆,爸爸先以150米/分的速度骑行一段时间,休息了5分钟,再以m米/分的速度到达图书馆,小军始终以同一速度骑行,两人行驶的路程y(米)与时间x(分钟)的关系如图,请结合图象,解答下列问题:
(1)a=?
________,b=
________,m=
________;
(2)若小军的速度是120米/分,求小军在途中与爸爸第二次相遇时,距图书馆的距离;
(3)在(2)的条件下,爸爸自第二次出发至到达图书馆前,何时与小军相距100米?
(4)若小军的行驶速度是v米/分,且在途中与爸爸恰好相遇两次(不包括家、图书馆两地),请直接写出v的取值范围.
17.一次函数y=kx+b的图象经过点A(0,9),并且与直线y=
x相交于点B,与x轴相交于点C
(1)若点B的横坐标为3,求点B的坐标和k,b的值
(2)在y轴上是否存在这样的点P,便得以点P,B,A为顶点的三角形是等腰三角形?若存在,请直接写出点P的坐标,若不存在,请说明理由。
(3)在直线y=kx+b上是否存在点Q,使△OBQ的面积等于
,若存在,请求出点Q的坐标,若不存在,请说明理由。
18.甲、乙两人在净月大街上同起点、同终点、同方向匀速步行2400米,先到终点的人原地休息.已知甲先出发4分钟,在整个步行过程中,甲、乙两人间的距离y(米)与甲出发的时间x(分)之间的关系如图中折线OA﹣AB﹣BC﹣CD所示.
(1)甲的速度为________米/分,乙的速度为________米/分.
(2)求线段AB的表达式,并写出自变量x的取值范围.
(3)求乙比甲早几分钟到达终点?
19.一辆客车从甲地开往乙地,一辆轿车从乙地开往甲地,两车同时出发,两车行驶x小时后,记客车离甲地的距离为y1千米,轿车离甲地的距离为y2千米,y1、y2关于x的函数图象如图
(1)根据图象,求出y1、y2关于x的函数关系式
(2)当两车相遇时,求此时客车行驶的时间;
(3)两车相距200千米时,求客车行驶的时间。
20.每年“双11"天猫商城都会推出各种优惠活动进行促销,今年,王阿姨的“双11“到来之前准备在两家天期店铺中选择一家购买原价均为10000元/条的被子2条和原价均为600元/个的颈椎枕若干个,已如网家店铺在活动明间分别给子以下优惠:
A店铺:"双11"当天购实所有商品可以享受8折优惠:
B店铺:买2条被子,赠送1个预椎枕、同时“双11"当天下单,还可立减160元;
设购买颈椎枕x(个),若王阿姨在“双11"当天下单,A,B两个店铺优惠后所付金额分别为yA(元)、yB(元)。
(1)试分别表示yA、yB与x的函数关系式;
(2)王阿姨准备在”双11"当天购买4个颈椎枕,通过计算说明在哪家店铺购买更省钱?
21.甲、乙两车同时从A地出发,沿同一路线各自匀速向B地行驶,甲到达B地停留1小时后按原路以另一速度匀速返回,直到与乙车相遇.乙车的速度为每小时60千米.两车之间的距离y(千米)与乙车行驶时间x(小时)之间的函数图象如图所示,则下列结论错误的是(???
)
A.?行驶3小时后,两车相距120千米
B.?甲车从A到B的速度为100千米/小时
C.?甲车返回是行驶的速度为95千米/小时
D.?A,B两地之间的距离为300千米
22.甲、乙两地高速铁路建设成功,一列动车从甲地开往乙地,
一列普通列车从乙地开往中地。两车均匀速行驶并同时出发,设普通列车行驶的时间为x(小时),两车之间的距离为y(千米),图中的折线表示y与x之间的函数关系,
下列结论:
①甲、乙两地相距1800千米
②点
B的实际意义是两车出发后4小时相遇
③动车的速度是280千米/小时
④m=6,n=900
其中正确的题________(写出所有正确结论的序号)
23.已知
与x成正比,当
时,
(1)求y与x之间的函数关系式,在下列坐标系中画出函数图象;
(2)当
时,求函数y的值;
(3)结合图象和函数的增减性,求当
时自变量x的取值范围.
答案解析部分
一、解答题
1.【答案】
(1)0.5;0.7;1
(2)0.3;0.06;0.1;6或62
(3)解:当
时,
;
当
时,
当
时,设
,将(23,0.7)(28,1)代入解析式
,解得
∴
.
2.【答案】
解:①设y1=kx,则将(10,600)代入得出:600=10k,
解得:k=60,
∴y1=60x
(0≤x≤10),
设y2=ax+b,则将(0,600),(6,0)代入得出:
,
解得:
,
∴y2=﹣100x+600
(0≤x≤6);
②当两车相遇时,y1=y2
,
即60x=﹣100x+600
解得:x=
;
∴当两车相遇时,此时客车行驶了
小时;
③相遇后相距200千米,则y1﹣y2=200,即60x+100x﹣600=200,
解得:x=5
5﹣
=
,
∴相遇后,两车相距200千米时,客车又行驶的时间
小时.
3.【答案】
(1)解:将点A(2,0)代入直线y=kx+3,得
0=2k+3,
解得k=-
,
∴y=-
x+3.
当x=0时,y=3.
∴B(0,3),OB=3.
当y=0时,-
x+3=0,
∴x=2,
∴A(2,0),OA=2,
∴S△AOB=
OA?OB=
×2×3=3
(2)解:如图2,
①当AB=BC时,点C与点A(2,0)关于y轴对称,故C(-2,0)符合题意;
②当AB=AC时,由A(2,0),B(0,3)得到AB=
=
,由AC=AC′=
得到C′(
+2,0)、C″(
-2,0).
综上所述,符合条件的点C的坐标是(-2,0)或(
+2,0)或(
-2,0)
(3)解:∵M(0,3),
∴OM=3,
∴AM=3-2=1.
由(1)知,S△AOB=3,
∴S△PBM=S△AOB=3;
①当点P在x轴下方时,S△PBM=S△PBM+S△APM=
+
?AM?|yP|=
+
×1×|yP|=3,
∴|yP|=3,
∵点P在x轴下方,
∴yP=-3.
当y=-3时,代入y=-
x+3得,-3=-
x+3,
解得x=4.
∴P(4,-3);
②当点P在x轴上方时,S△PBM=S△PBM-S△APM=
?AM?|yP|-
=
×1×|yP|-
=3,
∴|yP|=9,
∵点P在x轴上方,
∴yP=3.
当y=9时,代入y=-
x+3得,9=-
x+3,
解得x=-4.
∴P(-4,9).
4.【答案】
(1)(1)∵直线y=kx-3与y轴的交点为C(0,-3)
∴OC=3
∵
=
∴OB=
∴B点坐标为(
,0)
将B(
,0)代入y=kx-3,得
k-1=0
解得k=2.
(2)解:由(1)可知直线的解析式是y=2x-3,
S=
×OB×yA
=
×
×(2x-3)
=
x-
即:三角形AOB的面积S与x的函数关系式为S=
x-
,
当S=
时,
x-
=
,解得x=3,则2x-3=3,即A(3,3).
所以当点A的坐标为(3,3)时,△AOB的面积为
?
(3)解:存在.由(2)得A(3,3),AO=3
,∠AOB=45°,
当OP=AO=3
时,P(3
,0)或P(-3
,0);
当AP=OA=3
时,∠APO=∠AOP=45°,则OP=
OA=6,P(6,0);
当OP=AP时,P(3,0).
5.【答案】
(1)解:y=260000-[20x+32(6000-x)+8×6000]=12x+20000
自变量的取值范围是:0<x≤3000
(2)解:由题意,得12x+20000≥260000×16%,解得:x≥1800,
∴1800≤x≤3000,
购买甲种树苗不少于1800棵且不多于3000棵;
(3)解:①若成活率不低于93%且低于94%时,由题意得:
解得1200<x≤2400
在y=12x+20000中,∵12>0,∴y随x的增大而增大,
∴当x=2400时,y最大=48800,
②若成活率达到94%以上(含94%),则0.9x+0.95(6000-x)≥0.94×6000,解得:x≤1200,
由题意得y=12x+20000+260000×6%=12x+35600,
∵12>0,
∴y随x的增大而增大,
∴当x=1200时,y最大值=5000,
综上所述,50000>48800
∴购买甲种树苗1200棵,一种树苗4800棵,可获得最大利润,最大利润是50000元.
6.【答案】
(1)解:对于直线y=2x+2,当x=0时,y=2;当y=0时,x=-1
∴点A的坐标为(0,2),点B的坐标为(-1,0)
又∵CO=CD=4,
∴点D的坐标为(-4,4)
设直线AD的函数表达式为y=kx+b,则有
?,解得
,
∴直线AD的函数表达式为y=-
x+2;
(2)解:存在,共有四个点满足要求.
分别是P1(-4,9),P2(-4,-4),P3(-4,-1),P4(-4,
).
7.【答案】
(1)解:∵点A的坐标为(-6,0),
∴OA=6,
∵点P在直线
上,
∴可设点P的坐标为
,
∵直线
与x轴交于点E,和y轴交于点F,
∴点E、F的坐标分别为(-8,0)和(0,6),
∴当点P在第一、二象限时,△OPA的面积S=
·OA·
=
;
当点P在第三象限时,△OPA的面积S=
·OA·
=
;
∴点P运动过程中,△OPA的面积S与x的函数关系式是S=
或S=
(2)解:把S=
代入S=
和S=
得:
和
,
解得:
或
,
∴点P的坐标为
或
(3)解:假设存在P点,使△COD≌△FOE,则OD=OE=8,OC=OF=6,
①如图,
当点D在y轴的负半轴时,点C在x轴的负半轴,
∵OD=8,OC=6,
∴点D、C的坐标分别为(0,-8)和(-6,0),
设直线CD的解析式为:y=kx+b,则:
,解得
,
∴
,
由
,解得:
,
∴点P的坐标为
;
②如下图所示:当点D在y轴正半轴时,点C在x轴的正半轴,同理可解得此时点P的坐标为
;
综上所述,存在P点,使△COD≌△FOE,P的坐标是
或
8.【答案】
(1)解:3000÷(50﹣30)=3000÷20=150(米/分),
答:张强返回时的速度为150米/分。
(2)解:(45﹣30)×150=2250(米),点B的坐标为(45,750),
妈妈原来的速度为:2250÷45=50(米/分),
妈妈原来回家所用的时间为:3000÷50=60(分)
60﹣50=10(分),
答:妈妈比按原速返回提前10分钟到家。
(3)解:如图:
设线段BD的函数解析式为:y=kx+b,
把(0,3000),(45,750)代入得:
,解得:
,
∴y=﹣50x+3000,
线段OA的函数解析式为:y=100x(0≤x≤30),
设线段AC的解析式为:y=k1x+b1
,
把(30,3000),(50,0)代入得:
,解得:
,
∴y=﹣150x+7500,(30<x≤50)
当张强与妈妈相距1000米时,
即﹣50x+3000﹣100x=1000或100x﹣(﹣50x+3000)=1000或(﹣150x+7500)﹣(﹣50x+3000)=1000,
解得:x=35或x=
或x=
,
∴当时间为35分或
分或
分时,张强与妈妈何时相距1000米.
二、综合题
9.【答案】
(1)解:∵一次函数y=k1x+b过点A(-3,0);
C(3,4)
??????
∴
????
解得:
?
∴一次函数关系式为y=
x+2
∵正比例函数y=kx的图象过点为C(3,4)
∴4=-3k2
∴k2=
???
正比例函数:y=
x
(2)解:如图所示,作D1M⊥X轴于M点,作D2N⊥Y轴于N,在等腰△AD1B中,
?
A
D1=AB
;?
∠D1AB=90°??
∠D1DA=∠AOB=90°
∴∠D1AM+∠BAO=90°???
又∵∠ABO+∠BAO=90°
∴∠D1AM
=∠BAO
在△D1DA与△
OAB中
????
∠D1AM
=∠BAO(已证)
?????
∠D1MA=∠AOB(已证)
?????
A
D1=AB
(已证)
∴△D1MA≌△OAB(AAS)
∴D1
M=OA=3;AM=BO=2??
∴OM=5
∵D1在第二象限,∴D1(-5,3)
同理证:△D2NB≌△BOA(AAS)?
∴D2(-2,5)
(3)解:存在;作C关于X轴对称点C1
,
连接BC1
,
交X轴于E,此时△BCE周长最小。
∵
??????????????
∴
??
∴BC1的解析式为:y=-2x+2
令y=0,得0=-2x+2,??
x=1
∴E点的坐标为(1,0)
(4)解:P
(5,0)
????
P
(-5,0)
????
P?
(6,
0)
????
P?
(
,0)
10.【答案】
(1)解:设y甲=kx,
把(3,180)代入,得3k=180,解得k=60,
则y甲=60x;
设y乙=mx+n,
把(0,60),(3,180)代入,
得
,解得
,
则y乙=40x+60
(2)解:当x=1时,
y甲=60x=60,y乙=40x+60=100,
则MN=100﹣60=40(千米),
线段MN的实际意义:表示甲、乙两人出发1小时后,他们相距40千米
(3)解:分三种情况:
①当0<x≤3时,
(40x+60)﹣60x<30,解得x>1.5;
∴1.5<x≤3.
②当3<x≤5时,
60x﹣(40x+60)<30,解得x<4.5;
∴3<x≤4.5.
③当5<x≤6时,
300﹣(40x+60)<30,解得x>5.25.
∴5.25<x≤6.
综上所述,在乙行驶的过程中,当甲、乙两人距A地的路程差小于30千米时,x的取值范围是1.5<x<4.5或5.25<x≤6
11.【答案】
(1)解:∵OB=
,AO=6,∴AB=
=
,
∴∠BAO=30°,∴∠ABO=60°.
∵沿BE折叠O、D重合,
∴∠EBO=30°,OE=
BE,设OE=x,则(2x)2=x2+
,
∴x=2,即
BE=4,E(﹣2,0),设y=kx+b代入得:
,
解得:
,
∴直线BE的解析式是:
;
(2)解:过D作DG⊥OA于G.
∵沿BE折叠O、D重合,∴DE=2.
∵∠DAE=30°,∴∠DEA=60°,∠ADE=∠BOE=90°,
∴∠EDG=30°,
∴GE=1,DG=
,
∴OG=1+2=3
∴D的坐标是:D
;
(3)解:设P(x,0).
∵∠OAB=30°,DG=
,∴AD=2DG=
.分三种情况讨论:
①以A为圆心,AD为半径作圆与x轴交于点P,则AP=AD=
,∴P(
,0);
②以D为圆心,DA为半径作圆与x轴交于点P,则AP=2AG=
DG=6.
∵OA=6,∴P与O重合,∴P(0,0);
③设线段AD的垂直平分线交x轴于P,则PA=PD,
∴
,解得:x=-4,∴P(-4,0).
综上所述:P的坐标为:P(
,0)或P(0,0)或P(-4,0).
12.【答案】
(1)0.5;
(2)
(3)
13.【答案】
(1)30
(2)设乙前往A地的距离y(km)与乙行驶时间x(h)之间的关系式为y乙1=k1x,由题意,得
30=k1
,
∴y乙1=30x
设乙返回B地距离B地的距离y(km)与乙行驶时间x(h)之间的关系式为y乙2=k2x+b2
,
由题意,得
解得:
所以y=-30x+60
(3)由函数图象,得
(30+20)x=30,
解得x=0.6.
∴甲、乙第一次相遇是在出发后0.6小时
(4)
甲在修车前y与x之间的函数关系式为y甲1=kx+b,由题意,得;
解得:
y甲1=-20x+30,
设甲在修车后y与x之间的函数关系式为y甲2=k3x+b3
,
由题意,得
解得:
∴y甲2=-20x+40,
解得:
设乙前往A地的距离y(km)与乙行驶时间x(h)之间的关系式为y乙1=k1x,由题意,得
设乙返回B地距离B地的距离y(km)与乙行驶时间x(h)之间的关系式为y乙2=k2x+b2,由题意,
∴y=-30x+60.
当时
∴
14.【答案】
(1)解答:由函数图象,得图象表示了时间、距离的关系,自变量是时间,因变量是距离;
(2)解答:由纵坐标看出10时他距家15千米,13时他距家30千米;
(3)解答:由横坐标看出12:00时离家最远,由纵坐标看出离家30千米;
(4)解答:由纵坐标看出11时距家19千米,12时距家30千米,11时到12时他行驶了30-19=11(千米);
答:11时到12时他行驶了11千米.
(5)解答:由纵坐标看出12:00-13:00时距离没变且时间较长,得12:00-13:00休息并吃午饭;
(6)解答:由横坐标看出回家时用了2两小时,由纵坐标看出路程是30千米,回家的速度是30÷2=15(千米/小时)
答:他由离家最远的地方返回时的平均速度是15千米/小时。
15.【答案】
(1)解答:根据一次函数的定义,得:2-|m|=1,
解得m=±1.又∵m+1≠0即m≠-1,
∴当m=1,n为任意实数时,这个函数是一次函数;
(2)解答:根据正比例函数的定义,得:2-|m|=1,n+4=0,
解得m=±1,n=-4,
又∵m+1≠0即m≠-1,
∴当m=1,n=-4时,这个函数是正比例函数.
16.【答案】
(1)10;15;200
(2)解:线段BC所在直线的函数解析式为y=1500+200(x﹣15)=200x﹣1500;
线段OD所在的直线的函数解析式为y=120x.
联立两函数解析式成方程组,
,解得:
,
∴3000﹣2250=750(米).
答:小军在途中与爸爸第二次相遇时,距图书馆的距离是750米.
(3)解:根据题意得:|200x﹣1500﹣120x|=100,
解得:x1=
=17.5,x2=20.
答:爸爸自第二次出发至到达图书馆前,17.5分钟时和20分钟时与小军相距100米.
(4)解:当线段OD过点B时,小军的速度为1500÷15=100(米/分钟);
当线段OD过点C时,小军的速度为3000÷22.5=
(米/分钟).
结合图形可知,当100<v<
时,小军在途中与爸爸恰好相遇两次(不包括家、图书馆两地).
17.【答案】
(1)解:
∵B点的横坐标为3,
∴y=×3=5,
∴B(3,5),
又∵A(0,9),B(3,5)在y=kx+b上,
∴
,
解得:.
(2)解:
,解得
,即B(
,
),AB=
①以A为顶点时,P1(0.9+
)P20.9-
)
②以B为顶点时,P1(0,
)
③以P为顶点时,P1(0,
)
(3)解:①当点Q在点B右侧时,设Q(a,ka+9),C(-
,0)
S△OEQ=
,
.Q
②当点Q在点B左侧时,设Q(a,ka+9)
S△OEQ=
,a=
Q(
,
)
综上所述,Q
或Q(
,
)
18.【答案】
(1)60;80
(2)解:根据题意得:
设线段AB的表达式为:y=kx+b
,
把(4,240),(16,0)代入得:
,解得
,
即线段AB的表达式为:
;
(3)解:在B处甲乙相遇时,与出发点的距离为:240+(16﹣4)×60=960(米),
与终点的距离为:2400﹣960=1440(米),
相遇后,到达终点甲所用的时间为:
=24(分),
相遇后,到达终点乙所用的时间为:
=18(分),
24﹣18=6(分),
答:乙比甲早6分钟到达终点.
19.【答案】
(1)解:设y1=kx,则将(10,600)代入得出:
600=10k,
解得:k=60,
∴y1=60x(0≤x≤10),
设y2=ax+b,则将(0,600),(6,0)代入得出:
解得:
∴y2=-100x+600(0≤x≤6)
(2)解:当两车相遇时,y1=y2
,
即60x=-100x+600
解得:x=
∴当两车相遇时,求此时客车行驶了
小时
(3)解:若相遇前两车相距200千米,则y2-y1=200,
∴-100x+600
-
60x=
200,
解得:x=
若相遇后相距200千米,则y1-y2=200,即60x+100x-600=200,
解得:x=5
∴两车相距200千米时,客车行驶的时间为
小时或5小时
20.【答案】
(1)解:由题意得:
yA=1000×2×0.8+0.8×600x=480x+1600;
yB=
1000×2+600(x-1)-160=600x+1240
(2)解:当x=4时,ya=480×4+1600=3520;
yB=
600×4+1240=3640;
∵3520<3640,
∴在A店铺购买更省钱
三、单选题
21.【答案】
C
四、填空题
22.【答案】
①②④
五、作图题
23.【答案】
(1)解:设
,
当
时,
,
,解得
,
,
与x之间的函数关系式为
;
如图,
(2)解:当
时,
;
(3)解:当
时自变量x的取值范围为
.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
一次函数实际运用综合专项训练
1.在“看图说故事”活动中,某学习小组结合图象设计了一个问题情境.
已知小亮所在学校的宿舍、食堂、图书馆依次在同一条直线上,食堂离宿舍
,图书馆离宿舍
.周末,小亮从宿舍出发,匀速走了
到食堂;在食堂停留
吃早餐后,匀速走了
到图书馆;在图书馆停留
借书后,匀速走了
返回宿舍,给出的图象反映了这个过程中小亮离宿舍的距离
与离开宿舍的时间
之间的对应关系.
请根据相关信息,解答下列问题:
(1)填表:
离开宿舍的时间/
2
5
20
23
30
离宿舍的距离/
0.2
________
0.7
________
________
(2)填空:
①食堂到图书馆的距离为________
.
②小亮从食堂到图书馆的速度为________
.
③小亮从图书馆返回宿舍的速度为________
.
④当小亮离宿舍的距离为
时,他离开宿舍的时间为________
.
(3)当
时,请直接写出y关于x的函数解析式.
2.一辆客车从甲地开往乙地,一辆轿车从乙地开往甲地,两车同时出发,两车行驶x小时后,记客车离甲地的距离y1千米,轿车离甲地的距离y2千米,y1、y2关于x的函数图象如图所示:
①根据图象直接写出y1、y2关于x的函数关系式;
②当两车相遇时,求此时客车行驶的时间.
③相遇后,两车相距200千米时,求客车又行驶的时间.
3.如图(含备用图),在直角坐标系中,已知直线y=kx+3与x轴相交于点A(2,0),与y轴交于点B.
(1)求k的值及△AOB的面积;
(2)点C在x轴上,若△ABC是以AB为腰的等腰三角形,直接写出点C的坐标;
(3)点M(3,0)在x轴上,若点P是直线AB上的一个动点,当△PBM的面积与△AOB的面积相等时,求点P的坐标.
4.如图,直线y=kx-3与x轴、y轴分别交于点B,C,
=
.
(1)求点B坐标和k值;
(2)若点A(x,y)是直线y=kx-3上在第一象限内的一个动点,当点A在运动过程中,试写出△AOB的面积S与x的函数关系式(不要求写自变量范围);并进一步求出点A的坐标为多少时,△AOB的面积为
?
(3)在上述条件下,x轴上是否存在点P,使△AOP为等腰三角形?若存在,请写出满足条件的所有P点坐标;若不存在,请说明理由.
5.我市为创建“国家级森林城市”,政府决定对江边一处废弃荒地进行绿化,要求栽植甲、乙两种不同的树苗共6000棵,且甲种树苗不得多于乙种树苗.某承包商以26万元的报价中标承包了这项工程.根据调查及相关资料表明:移栽一棵树苗的平均费用为8元,甲、乙两种树苗的购买价及成活率如表:
品种
购买价(元/棵)
成活率
甲
20
90%
乙
32
95%
设购买甲种树苗x棵,承包商获得的利润为y元.请根据以上信息解答下列问题:
(1)设y与x之间的函数关系式,并写出自变量x的取值范围;
(2)承包商要获得不低于中标价16%的利润,应如何选购树苗?
(3)政府与承包商的合同要求,栽植这批树苗的成活率必须不低于93%,否则承包商出资补栽;若成货率达到94%以上(含94%),则政府另给予工程款总额6%的奖励,该承包商应如何选购树苗才能获得最大利润?最大利润是多少?
6.如图,在平面直角坐标系xOy中,直线y=2x+2与y轴交于点A,与x轴交于点B.直线l⊥x轴负半轴于点C,点D是直线l上一点且位于x轴上方.已知CO=CD=4.
(1)求经过A,D两点的直线的函数关系式和点B的坐标;
(2)在直线l上是否存在点P使得△BDP为等腰三角形,若存在,直接写出P点坐标,若不存在,请说明理由.
7.如图,直线y=
x+6与x轴、y轴分别相交于点E、F,点A的坐标为(-6,0),P(x,y)是直线y=
x+6上一个动点.
(1)在点P运动过程中,试写出△OPA的面积s与x的函数关系式;
(2)当P运动到什么位置,△OPA的面积为
,求出此时点P的坐标;
(3)过P作EF的垂线分别交x轴、y轴于C、D.是否存在这样的点P,使△COD≌△FOE?若存在,直接写出此时点P的坐标(不要求写解答过程);若不存在,请说明理由.
8.某天早晨,张强从家跑步去体育锻炼,同时妈妈从体育场晨练结束回家,途中两人相遇,张强跑到体育场后发现要下雨,立即按原路返回,遇到妈妈后两人一起回到家(张强和妈妈始终在同一条笔直的公路上行走).如图是两人离家的距离y(米)与张强出发的时间x(分)之间的函数图象,根据图象信息解答下列问题:
(1)求张强返回时的速度;
(2)妈妈比按原速返回提前多少分钟到家?
(3)请直接写出张强与妈妈何时相距1000米?
9.如图,在平面直角坐标系xOy中,一次函数y=k1x+b的图象与x轴交于点A(-3,0),与y轴交于点B,且与正比例函数y=kx的图象交点为C(3,4).
(1)求正比例函数与一次函数的关系式;
(2)若点D在第二象限,△DAB是以AB为直角边的等腰直角三角形,请求出点D的坐标;
(3)在x轴上是否存在一点E使△BCE周长最小,若存在,求出点E的坐标
在x轴上求一点P使△POC为等腰三角形,请直接写出所有符合条件的点P的坐标.
10.甲、乙两人利用不同的交通工具,沿同一路线分别从A、B两地同时出发匀速前往C地(B在A、C两地的途中).设甲、乙两车距A地的路程分别为y甲、y乙(千米),行驶的时间为x(小时),y甲、y乙与x之间的函数图象如图所示.
(1)直接写出y甲、y乙与x之间的函数表达式;
(2)如图,过点(1,0)作x轴的垂线,分别交y甲、y乙的图象于点M,N.求线段MN的长,并解释线段MN的实际意义;
(3)在乙行驶的过程中,当甲、乙两人距A地的路程差小于30千米时,求x的取值范围.
11.如图,Rt△AOB?在平面直角坐标系中,点O与坐标原点重合,点A在x轴上,点B在y轴上,
,将△AOB沿直线BE折叠,使得OB边落在AB上,点O与点D重合.
(1)求直线BE的解析式;
(2)求点D的坐标;
(3)x轴上是否存在点P,使△PAD为等腰三角形?若存在,请直接写出点P的坐标,若不存在,请说明理由。
12.小李和小陆从
A
地出发,骑自行车沿同一条路行驶到
B
地,他们离出发地的距离s和行驶时间t之间的关系的图象如图,根据图象回答下列问题:
(1)小李在途中逗留的时间为________h,小陆从
A
地到
B
地的速度是________km/h.
(2)当小李和小陆相遇时,他们离
B
地的路程是________千米;
(3)写出小李在逗留之前离
A
地的路程s和行驶时间t之间的函数关系式为________
13.在一条笔直的公路上有A、B两地.甲、乙两人同时出发,甲骑电动车从A地到B地,中途出现故障后停车维修,修好车后以原速继续行驶到B地;乙骑摩托车从B地到A地,到达A地后立即按原原速返回,结果两人同时到B地.如图是甲、乙两人与B地的距离y(km)与乙行驶时间x(h)之间的函数图象。
(1)A、B两地间的距离为________km;
(2)求乙与B地的距离y(km)与乙行驶时间x(h)之间的函数关系式;
(3)求甲、乙第一次相遇的时间;
(4)若两人之间的距离不超过10km时,能够用无线对讲机保持联系,请求出乙在行进中能用无线对讲机与甲保持联系的x取值范围。
14.小明某天上午9时骑自行车离开家,15时回家,他有意描绘了离家的距离与时间的变化情况(如图所示)
(1)图象表示了哪两个变量的关系?哪个是自变量?哪个是因变量?
(2)10时和13时,他分别离家多远?
(3)他到达离家最远的地方是什么时间?离家多远?
(4)11时到12时他行驶了多少千米?
(5)他可能在哪段时间内休息,并吃午餐?
(6)他由离家最远的地方返回时的平均速度是多少?
15.已知y=(m+1)x2-|m|+n+4
(1)当m、n取何值时,y是x的一次函数?
(2)当m、n取何值时,y是x的正比例函数?
16.“低碳环保,绿色出行”的理念得到广大群众的接受,越来越多的人再次选择自行车作为出行工具,小军和爸爸同时从家骑自行车去图书馆,爸爸先以150米/分的速度骑行一段时间,休息了5分钟,再以m米/分的速度到达图书馆,小军始终以同一速度骑行,两人行驶的路程y(米)与时间x(分钟)的关系如图,请结合图象,解答下列问题:
(1)a=?
________,b=
________,m=
________;
(2)若小军的速度是120米/分,求小军在途中与爸爸第二次相遇时,距图书馆的距离;
(3)在(2)的条件下,爸爸自第二次出发至到达图书馆前,何时与小军相距100米?
(4)若小军的行驶速度是v米/分,且在途中与爸爸恰好相遇两次(不包括家、图书馆两地),请直接写出v的取值范围.
17.一次函数y=kx+b的图象经过点A(0,9),并且与直线y=
x相交于点B,与x轴相交于点C
(1)若点B的横坐标为3,求点B的坐标和k,b的值
(2)在y轴上是否存在这样的点P,便得以点P,B,A为顶点的三角形是等腰三角形?若存在,请直接写出点P的坐标,若不存在,请说明理由。
(3)在直线y=kx+b上是否存在点Q,使△OBQ的面积等于
,若存在,请求出点Q的坐标,若不存在,请说明理由。
18.甲、乙两人在净月大街上同起点、同终点、同方向匀速步行2400米,先到终点的人原地休息.已知甲先出发4分钟,在整个步行过程中,甲、乙两人间的距离y(米)与甲出发的时间x(分)之间的关系如图中折线OA﹣AB﹣BC﹣CD所示.
(1)甲的速度为________米/分,乙的速度为________米/分.
(2)求线段AB的表达式,并写出自变量x的取值范围.
(3)求乙比甲早几分钟到达终点?
19.一辆客车从甲地开往乙地,一辆轿车从乙地开往甲地,两车同时出发,两车行驶x小时后,记客车离甲地的距离为y1千米,轿车离甲地的距离为y2千米,y1、y2关于x的函数图象如图
(1)根据图象,求出y1、y2关于x的函数关系式
(2)当两车相遇时,求此时客车行驶的时间;
(3)两车相距200千米时,求客车行驶的时间。
20.每年“双11"天猫商城都会推出各种优惠活动进行促销,今年,王阿姨的“双11“到来之前准备在两家天期店铺中选择一家购买原价均为10000元/条的被子2条和原价均为600元/个的颈椎枕若干个,已如网家店铺在活动明间分别给子以下优惠:
A店铺:"双11"当天购实所有商品可以享受8折优惠:
B店铺:买2条被子,赠送1个预椎枕、同时“双11"当天下单,还可立减160元;
设购买颈椎枕x(个),若王阿姨在“双11"当天下单,A,B两个店铺优惠后所付金额分别为yA(元)、yB(元)。
(1)试分别表示yA、yB与x的函数关系式;
(2)王阿姨准备在”双11"当天购买4个颈椎枕,通过计算说明在哪家店铺购买更省钱?
21.甲、乙两车同时从A地出发,沿同一路线各自匀速向B地行驶,甲到达B地停留1小时后按原路以另一速度匀速返回,直到与乙车相遇.乙车的速度为每小时60千米.两车之间的距离y(千米)与乙车行驶时间x(小时)之间的函数图象如图所示,则下列结论错误的是(???
)
A.?行驶3小时后,两车相距120千米
B.?甲车从A到B的速度为100千米/小时
C.?甲车返回是行驶的速度为95千米/小时
D.?A,B两地之间的距离为300千米
22.甲、乙两地高速铁路建设成功,一列动车从甲地开往乙地,
一列普通列车从乙地开往中地。两车均匀速行驶并同时出发,设普通列车行驶的时间为x(小时),两车之间的距离为y(千米),图中的折线表示y与x之间的函数关系,
下列结论:
①甲、乙两地相距1800千米
②点
B的实际意义是两车出发后4小时相遇
③动车的速度是280千米/小时
④m=6,n=900
其中正确的题________(写出所有正确结论的序号)
23.已知
与x成正比,当
时,
(1)求y与x之间的函数关系式,在下列坐标系中画出函数图象;
(2)当
时,求函数y的值;
(3)结合图象和函数的增减性,求当
时自变量x的取值范围.
答案解析部分
一、解答题
1.【答案】
(1)0.5;0.7;1
(2)0.3;0.06;0.1;6或62
(3)解:当
时,
;
当
时,
当
时,设
,将(23,0.7)(28,1)代入解析式
,解得
∴
.
2.【答案】
解:①设y1=kx,则将(10,600)代入得出:600=10k,
解得:k=60,
∴y1=60x
(0≤x≤10),
设y2=ax+b,则将(0,600),(6,0)代入得出:
,
解得:
,
∴y2=﹣100x+600
(0≤x≤6);
②当两车相遇时,y1=y2
,
即60x=﹣100x+600
解得:x=
;
∴当两车相遇时,此时客车行驶了
小时;
③相遇后相距200千米,则y1﹣y2=200,即60x+100x﹣600=200,
解得:x=5
5﹣
=
,
∴相遇后,两车相距200千米时,客车又行驶的时间
小时.
3.【答案】
(1)解:将点A(2,0)代入直线y=kx+3,得
0=2k+3,
解得k=-
,
∴y=-
x+3.
当x=0时,y=3.
∴B(0,3),OB=3.
当y=0时,-
x+3=0,
∴x=2,
∴A(2,0),OA=2,
∴S△AOB=
OA?OB=
×2×3=3
(2)解:如图2,
①当AB=BC时,点C与点A(2,0)关于y轴对称,故C(-2,0)符合题意;
②当AB=AC时,由A(2,0),B(0,3)得到AB=
=
,由AC=AC′=
得到C′(
+2,0)、C″(
-2,0).
综上所述,符合条件的点C的坐标是(-2,0)或(
+2,0)或(
-2,0)
(3)解:∵M(0,3),
∴OM=3,
∴AM=3-2=1.
由(1)知,S△AOB=3,
∴S△PBM=S△AOB=3;
①当点P在x轴下方时,S△PBM=S△PBM+S△APM=
+
?AM?|yP|=
+
×1×|yP|=3,
∴|yP|=3,
∵点P在x轴下方,
∴yP=-3.
当y=-3时,代入y=-
x+3得,-3=-
x+3,
解得x=4.
∴P(4,-3);
②当点P在x轴上方时,S△PBM=S△PBM-S△APM=
?AM?|yP|-
=
×1×|yP|-
=3,
∴|yP|=9,
∵点P在x轴上方,
∴yP=3.
当y=9时,代入y=-
x+3得,9=-
x+3,
解得x=-4.
∴P(-4,9).
4.【答案】
(1)(1)∵直线y=kx-3与y轴的交点为C(0,-3)
∴OC=3
∵
=
∴OB=
∴B点坐标为(
,0)
将B(
,0)代入y=kx-3,得
k-1=0
解得k=2.
(2)解:由(1)可知直线的解析式是y=2x-3,
S=
×OB×yA
=
×
×(2x-3)
=
x-
即:三角形AOB的面积S与x的函数关系式为S=
x-
,
当S=
时,
x-
=
,解得x=3,则2x-3=3,即A(3,3).
所以当点A的坐标为(3,3)时,△AOB的面积为
?
(3)解:存在.由(2)得A(3,3),AO=3
,∠AOB=45°,
当OP=AO=3
时,P(3
,0)或P(-3
,0);
当AP=OA=3
时,∠APO=∠AOP=45°,则OP=
OA=6,P(6,0);
当OP=AP时,P(3,0).
5.【答案】
(1)解:y=260000-[20x+32(6000-x)+8×6000]=12x+20000
自变量的取值范围是:0<x≤3000
(2)解:由题意,得12x+20000≥260000×16%,解得:x≥1800,
∴1800≤x≤3000,
购买甲种树苗不少于1800棵且不多于3000棵;
(3)解:①若成活率不低于93%且低于94%时,由题意得:
解得1200<x≤2400
在y=12x+20000中,∵12>0,∴y随x的增大而增大,
∴当x=2400时,y最大=48800,
②若成活率达到94%以上(含94%),则0.9x+0.95(6000-x)≥0.94×6000,解得:x≤1200,
由题意得y=12x+20000+260000×6%=12x+35600,
∵12>0,
∴y随x的增大而增大,
∴当x=1200时,y最大值=5000,
综上所述,50000>48800
∴购买甲种树苗1200棵,一种树苗4800棵,可获得最大利润,最大利润是50000元.
6.【答案】
(1)解:对于直线y=2x+2,当x=0时,y=2;当y=0时,x=-1
∴点A的坐标为(0,2),点B的坐标为(-1,0)
又∵CO=CD=4,
∴点D的坐标为(-4,4)
设直线AD的函数表达式为y=kx+b,则有
?,解得
,
∴直线AD的函数表达式为y=-
x+2;
(2)解:存在,共有四个点满足要求.
分别是P1(-4,9),P2(-4,-4),P3(-4,-1),P4(-4,
).
7.【答案】
(1)解:∵点A的坐标为(-6,0),
∴OA=6,
∵点P在直线
上,
∴可设点P的坐标为
,
∵直线
与x轴交于点E,和y轴交于点F,
∴点E、F的坐标分别为(-8,0)和(0,6),
∴当点P在第一、二象限时,△OPA的面积S=
·OA·
=
;
当点P在第三象限时,△OPA的面积S=
·OA·
=
;
∴点P运动过程中,△OPA的面积S与x的函数关系式是S=
或S=
(2)解:把S=
代入S=
和S=
得:
和
,
解得:
或
,
∴点P的坐标为
或
(3)解:假设存在P点,使△COD≌△FOE,则OD=OE=8,OC=OF=6,
①如图,
当点D在y轴的负半轴时,点C在x轴的负半轴,
∵OD=8,OC=6,
∴点D、C的坐标分别为(0,-8)和(-6,0),
设直线CD的解析式为:y=kx+b,则:
,解得
,
∴
,
由
,解得:
,
∴点P的坐标为
;
②如下图所示:当点D在y轴正半轴时,点C在x轴的正半轴,同理可解得此时点P的坐标为
;
综上所述,存在P点,使△COD≌△FOE,P的坐标是
或
8.【答案】
(1)解:3000÷(50﹣30)=3000÷20=150(米/分),
答:张强返回时的速度为150米/分。
(2)解:(45﹣30)×150=2250(米),点B的坐标为(45,750),
妈妈原来的速度为:2250÷45=50(米/分),
妈妈原来回家所用的时间为:3000÷50=60(分)
60﹣50=10(分),
答:妈妈比按原速返回提前10分钟到家。
(3)解:如图:
设线段BD的函数解析式为:y=kx+b,
把(0,3000),(45,750)代入得:
,解得:
,
∴y=﹣50x+3000,
线段OA的函数解析式为:y=100x(0≤x≤30),
设线段AC的解析式为:y=k1x+b1
,
把(30,3000),(50,0)代入得:
,解得:
,
∴y=﹣150x+7500,(30<x≤50)
当张强与妈妈相距1000米时,
即﹣50x+3000﹣100x=1000或100x﹣(﹣50x+3000)=1000或(﹣150x+7500)﹣(﹣50x+3000)=1000,
解得:x=35或x=
或x=
,
∴当时间为35分或
分或
分时,张强与妈妈何时相距1000米.
二、综合题
9.【答案】
(1)解:∵一次函数y=k1x+b过点A(-3,0);
C(3,4)
??????
∴
????
解得:
?
∴一次函数关系式为y=
x+2
∵正比例函数y=kx的图象过点为C(3,4)
∴4=-3k2
∴k2=
???
正比例函数:y=
x
(2)解:如图所示,作D1M⊥X轴于M点,作D2N⊥Y轴于N,在等腰△AD1B中,
?
A
D1=AB
;?
∠D1AB=90°??
∠D1DA=∠AOB=90°
∴∠D1AM+∠BAO=90°???
又∵∠ABO+∠BAO=90°
∴∠D1AM
=∠BAO
在△D1DA与△
OAB中
????
∠D1AM
=∠BAO(已证)
?????
∠D1MA=∠AOB(已证)
?????
A
D1=AB
(已证)
∴△D1MA≌△OAB(AAS)
∴D1
M=OA=3;AM=BO=2??
∴OM=5
∵D1在第二象限,∴D1(-5,3)
同理证:△D2NB≌△BOA(AAS)?
∴D2(-2,5)
(3)解:存在;作C关于X轴对称点C1
,
连接BC1
,
交X轴于E,此时△BCE周长最小。
∵
??????????????
∴
??
∴BC1的解析式为:y=-2x+2
令y=0,得0=-2x+2,??
x=1
∴E点的坐标为(1,0)
(4)解:P
(5,0)
????
P
(-5,0)
????
P?
(6,
0)
????
P?
(
,0)
10.【答案】
(1)解:设y甲=kx,
把(3,180)代入,得3k=180,解得k=60,
则y甲=60x;
设y乙=mx+n,
把(0,60),(3,180)代入,
得
,解得
,
则y乙=40x+60
(2)解:当x=1时,
y甲=60x=60,y乙=40x+60=100,
则MN=100﹣60=40(千米),
线段MN的实际意义:表示甲、乙两人出发1小时后,他们相距40千米
(3)解:分三种情况:
①当0<x≤3时,
(40x+60)﹣60x<30,解得x>1.5;
∴1.5<x≤3.
②当3<x≤5时,
60x﹣(40x+60)<30,解得x<4.5;
∴3<x≤4.5.
③当5<x≤6时,
300﹣(40x+60)<30,解得x>5.25.
∴5.25<x≤6.
综上所述,在乙行驶的过程中,当甲、乙两人距A地的路程差小于30千米时,x的取值范围是1.5<x<4.5或5.25<x≤6
11.【答案】
(1)解:∵OB=
,AO=6,∴AB=
=
,
∴∠BAO=30°,∴∠ABO=60°.
∵沿BE折叠O、D重合,
∴∠EBO=30°,OE=
BE,设OE=x,则(2x)2=x2+
,
∴x=2,即
BE=4,E(﹣2,0),设y=kx+b代入得:
,
解得:
,
∴直线BE的解析式是:
;
(2)解:过D作DG⊥OA于G.
∵沿BE折叠O、D重合,∴DE=2.
∵∠DAE=30°,∴∠DEA=60°,∠ADE=∠BOE=90°,
∴∠EDG=30°,
∴GE=1,DG=
,
∴OG=1+2=3
∴D的坐标是:D
;
(3)解:设P(x,0).
∵∠OAB=30°,DG=
,∴AD=2DG=
.分三种情况讨论:
①以A为圆心,AD为半径作圆与x轴交于点P,则AP=AD=
,∴P(
,0);
②以D为圆心,DA为半径作圆与x轴交于点P,则AP=2AG=
DG=6.
∵OA=6,∴P与O重合,∴P(0,0);
③设线段AD的垂直平分线交x轴于P,则PA=PD,
∴
,解得:x=-4,∴P(-4,0).
综上所述:P的坐标为:P(
,0)或P(0,0)或P(-4,0).
12.【答案】
(1)0.5;
(2)
(3)
13.【答案】
(1)30
(2)设乙前往A地的距离y(km)与乙行驶时间x(h)之间的关系式为y乙1=k1x,由题意,得
30=k1
,
∴y乙1=30x
设乙返回B地距离B地的距离y(km)与乙行驶时间x(h)之间的关系式为y乙2=k2x+b2
,
由题意,得
解得:
所以y=-30x+60
(3)由函数图象,得
(30+20)x=30,
解得x=0.6.
∴甲、乙第一次相遇是在出发后0.6小时
(4)
甲在修车前y与x之间的函数关系式为y甲1=kx+b,由题意,得;
解得:
y甲1=-20x+30,
设甲在修车后y与x之间的函数关系式为y甲2=k3x+b3
,
由题意,得
解得:
∴y甲2=-20x+40,
解得:
设乙前往A地的距离y(km)与乙行驶时间x(h)之间的关系式为y乙1=k1x,由题意,得
设乙返回B地距离B地的距离y(km)与乙行驶时间x(h)之间的关系式为y乙2=k2x+b2,由题意,
∴y=-30x+60.
当时
∴
14.【答案】
(1)解答:由函数图象,得图象表示了时间、距离的关系,自变量是时间,因变量是距离;
(2)解答:由纵坐标看出10时他距家15千米,13时他距家30千米;
(3)解答:由横坐标看出12:00时离家最远,由纵坐标看出离家30千米;
(4)解答:由纵坐标看出11时距家19千米,12时距家30千米,11时到12时他行驶了30-19=11(千米);
答:11时到12时他行驶了11千米.
(5)解答:由纵坐标看出12:00-13:00时距离没变且时间较长,得12:00-13:00休息并吃午饭;
(6)解答:由横坐标看出回家时用了2两小时,由纵坐标看出路程是30千米,回家的速度是30÷2=15(千米/小时)
答:他由离家最远的地方返回时的平均速度是15千米/小时。
15.【答案】
(1)解答:根据一次函数的定义,得:2-|m|=1,
解得m=±1.又∵m+1≠0即m≠-1,
∴当m=1,n为任意实数时,这个函数是一次函数;
(2)解答:根据正比例函数的定义,得:2-|m|=1,n+4=0,
解得m=±1,n=-4,
又∵m+1≠0即m≠-1,
∴当m=1,n=-4时,这个函数是正比例函数.
16.【答案】
(1)10;15;200
(2)解:线段BC所在直线的函数解析式为y=1500+200(x﹣15)=200x﹣1500;
线段OD所在的直线的函数解析式为y=120x.
联立两函数解析式成方程组,
,解得:
,
∴3000﹣2250=750(米).
答:小军在途中与爸爸第二次相遇时,距图书馆的距离是750米.
(3)解:根据题意得:|200x﹣1500﹣120x|=100,
解得:x1=
=17.5,x2=20.
答:爸爸自第二次出发至到达图书馆前,17.5分钟时和20分钟时与小军相距100米.
(4)解:当线段OD过点B时,小军的速度为1500÷15=100(米/分钟);
当线段OD过点C时,小军的速度为3000÷22.5=
(米/分钟).
结合图形可知,当100<v<
时,小军在途中与爸爸恰好相遇两次(不包括家、图书馆两地).
17.【答案】
(1)解:
∵B点的横坐标为3,
∴y=×3=5,
∴B(3,5),
又∵A(0,9),B(3,5)在y=kx+b上,
∴
,
解得:.
(2)解:
,解得
,即B(
,
),AB=
①以A为顶点时,P1(0.9+
)P20.9-
)
②以B为顶点时,P1(0,
)
③以P为顶点时,P1(0,
)
(3)解:①当点Q在点B右侧时,设Q(a,ka+9),C(-
,0)
S△OEQ=
,
.Q
②当点Q在点B左侧时,设Q(a,ka+9)
S△OEQ=
,a=
Q(
,
)
综上所述,Q
或Q(
,
)
18.【答案】
(1)60;80
(2)解:根据题意得:
设线段AB的表达式为:y=kx+b
,
把(4,240),(16,0)代入得:
,解得
,
即线段AB的表达式为:
;
(3)解:在B处甲乙相遇时,与出发点的距离为:240+(16﹣4)×60=960(米),
与终点的距离为:2400﹣960=1440(米),
相遇后,到达终点甲所用的时间为:
=24(分),
相遇后,到达终点乙所用的时间为:
=18(分),
24﹣18=6(分),
答:乙比甲早6分钟到达终点.
19.【答案】
(1)解:设y1=kx,则将(10,600)代入得出:
600=10k,
解得:k=60,
∴y1=60x(0≤x≤10),
设y2=ax+b,则将(0,600),(6,0)代入得出:
解得:
∴y2=-100x+600(0≤x≤6)
(2)解:当两车相遇时,y1=y2
,
即60x=-100x+600
解得:x=
∴当两车相遇时,求此时客车行驶了
小时
(3)解:若相遇前两车相距200千米,则y2-y1=200,
∴-100x+600
-
60x=
200,
解得:x=
若相遇后相距200千米,则y1-y2=200,即60x+100x-600=200,
解得:x=5
∴两车相距200千米时,客车行驶的时间为
小时或5小时
20.【答案】
(1)解:由题意得:
yA=1000×2×0.8+0.8×600x=480x+1600;
yB=
1000×2+600(x-1)-160=600x+1240
(2)解:当x=4时,ya=480×4+1600=3520;
yB=
600×4+1240=3640;
∵3520<3640,
∴在A店铺购买更省钱
三、单选题
21.【答案】
C
四、填空题
22.【答案】
①②④
五、作图题
23.【答案】
(1)解:设
,
当
时,
,
,解得
,
,
与x之间的函数关系式为
;
如图,
(2)解:当
时,
;
(3)解:当
时自变量x的取值范围为
.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
