一元一次方程解法复习

(共22张PPT)
一听就懂
一做就错
查找错误
分析错因
反思整改
轻轻松松解方程
高高兴兴得答案
问题
寻求
策略
解决
问题
解：方程两边同时除以 – 3，
得
解方程：
对吗？
错
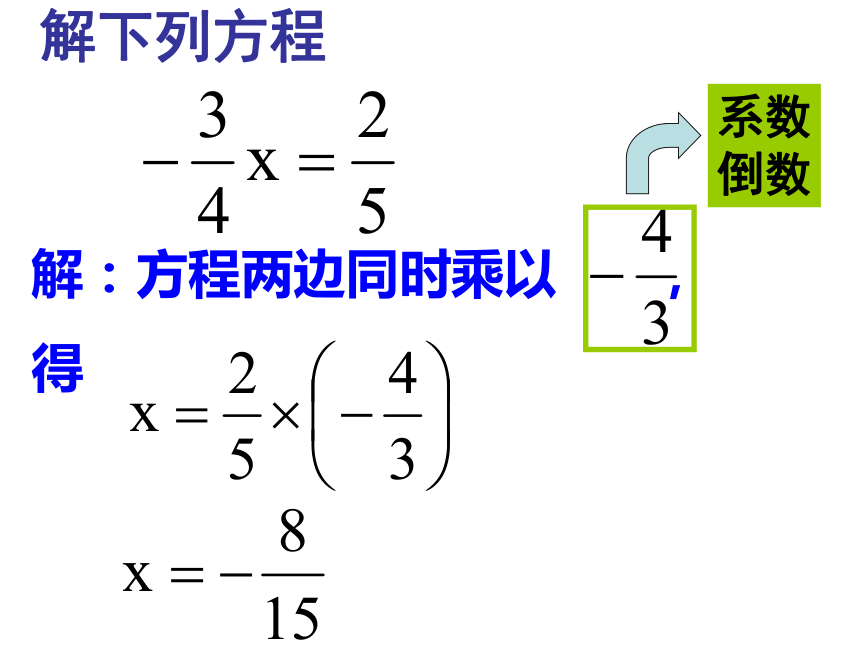
解下列方程
解：方程两边同时乘以 ，
得
系数
倒数
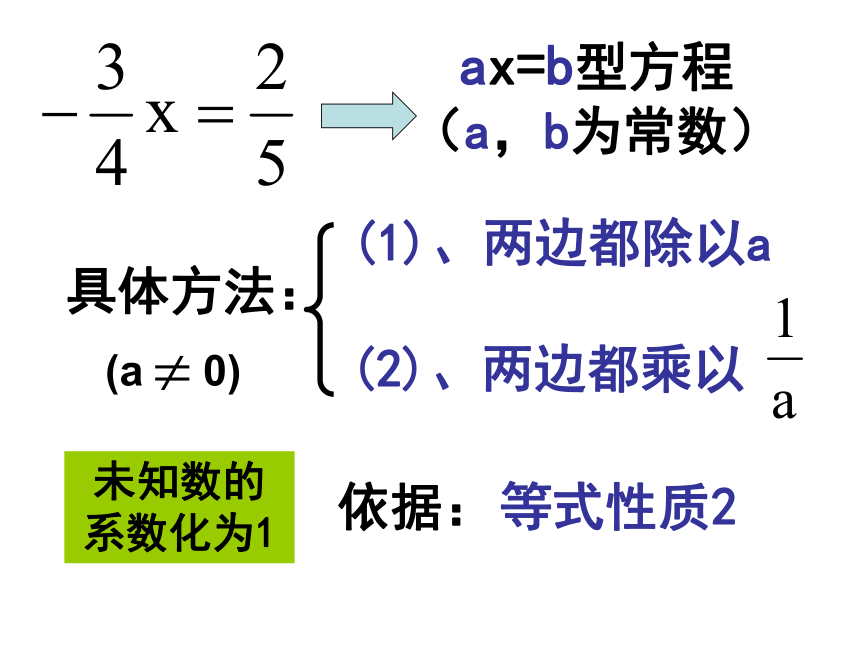
ax=b型方程
（a，b为常数）
具体方法：
(1)、两边都除以a
(2)、两边都乘以
(a 0)
未知数的
系数化为1
依据：
等式性质2
５X＝３X＋４
解：5x-3x=4
移项
移项要变号
等式性质1
2x =4
x =2
在括号中填上变形名称。
（ ）
依据：
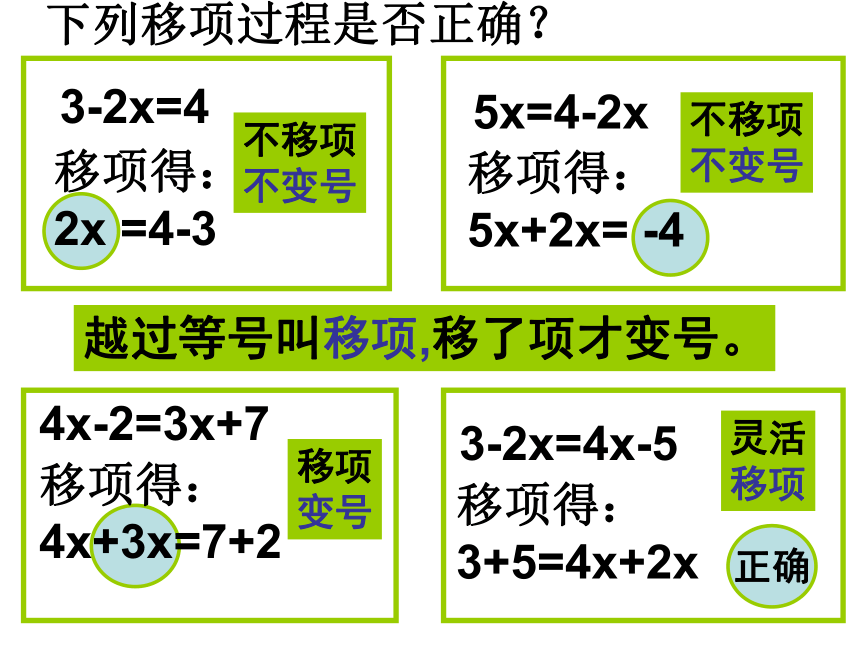
下列移项过程是否正确？
3-2x=4
移项得：
2x =4-3
5x=4-2x
移项得：
5x+2x= -4
4x-2=3x+7
移项得：
4x+3x=7+2
3-2x=4x-5
移项得：
3+5=4x+2x
不移项
不变号
不移项
不变号
移项
变号
灵活
移项
越过等号叫移项,移了项才变号。
正确
去括号：4x-2x -2 =8
下列方程的变形过程是否正确？
4x-2（x-1）=8
去括号：2x-4-12x +10 = 9
注意
变号
防止
漏乘
下列方程
去分母后的结果是（ ）
A、3（3x-1）-（5+2x）= x
B、9x-3-5+2x=6x
D、3（3x-1）-（5+2x)=6x
C、9x-1 -5-2x= x
D
去分母时要注意什么？
每项都要乘，
分子添括号
等式性质2
依据：
小明和小刚在解下列方程时发生了争论：
小明认为：分母先化为整数，得
而小刚认为：等号右边的1在分母化整数
时保持不变，并且等号左边的第二个式子
只要分子分母同时乘以10就够了。
你能对这两位同学的争论做出评论吗？
小明反驳到：不是说每一项都要乘吗？
分母化整数要注意什么？
分数的基本性质
与分子分母有关，其他项无关；
而去分母时，每一项都要乘。
分母化整数依据：
( )
( )
( )
( )
( )
去分母
去括号
移 项
合并同类项
未知数系数化为1
解：
( )
分母化整数
括号中写出
变形名称
解一元一次方程的一般步骤：
步 骤
注意事项
去分母
去括号
移项
合并同类项
系数化为1
注意变号，防止漏乘
移项要变号，没移不变号
系数相加减，字母指数不要变
除以系数或乘以系数的倒数
分母化整数
每项都要乘，分子添括号
与分子分母有关，其他项无关
自我检测：解下列方程（5分钟）
答案：
四人小组合作、诊断错误（5分钟）
（由组长批改并汇报整组错误情况）
小组讨论、诊断错误（5分钟）
（由组长批改并汇报整组错误情况）
错误1（变形名称）： ；
注意事项： 。
错误2（变形名称）： ；
注意事项： 。
其他错误： ；
注意事项： 。
小彬解方程 ，
去分母时方程左边的1没有乘以10，由此求得方程的解为x=4。试求a的值，并正确求出方程的解。
（将错就错法）
解：小彬去分母得：
2（2x-1）+1=5（x+a）
将x=4代入上面的方程得：
a=-1
X=13
将a=-1代回方程：
用合适的方法解方程：
（小组讨论）
解：方程两边同乘以9
？
X=2
从外层向里层依次去括号。
运用等式性质2
则原方程可化为：
2y-7=5y- 4（-y）
y=-1
则：
体现了数学中
的整体思想
换元法
通过这节课的学习，
谈谈你的最大收获？