一次函数与反比例函数的交点的问题(九年级数学综合实践课)
文档属性
| 名称 | 一次函数与反比例函数的交点的问题(九年级数学综合实践课) | 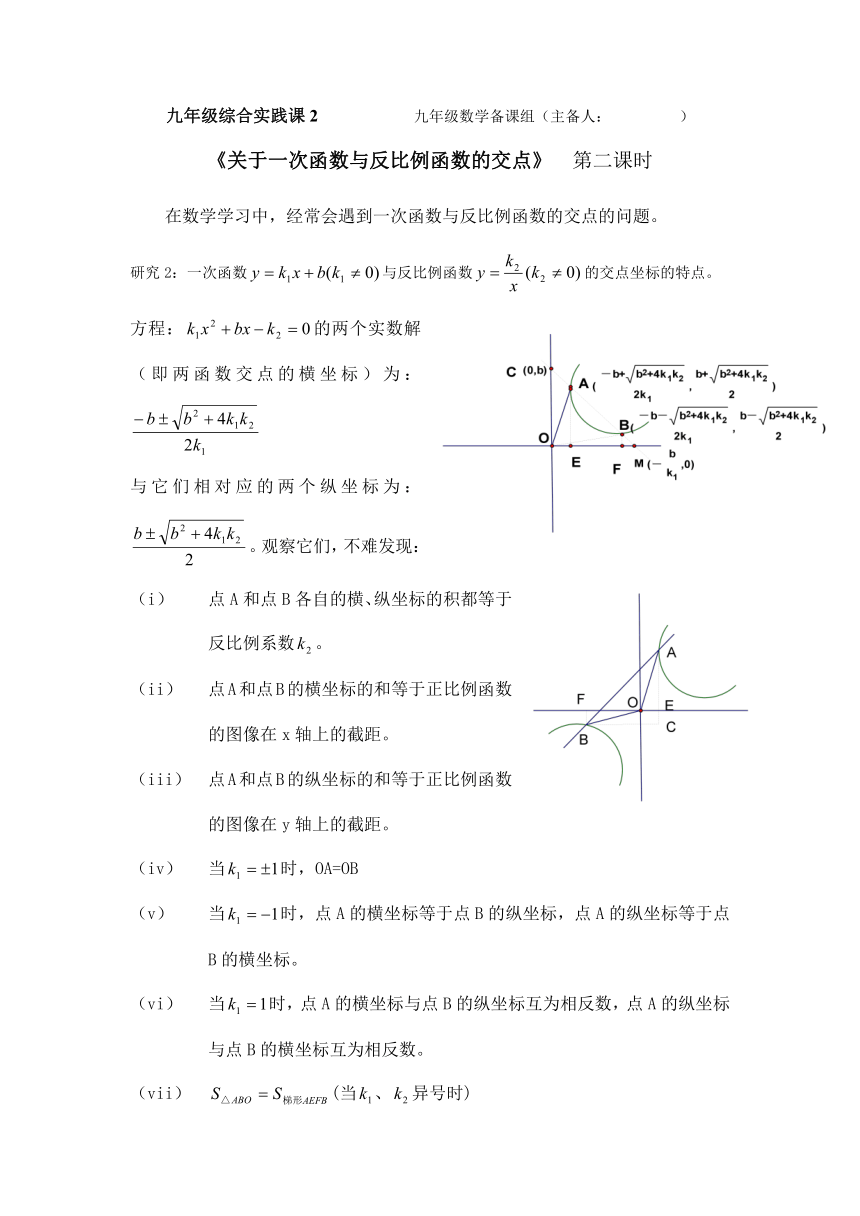 | |
| 格式 | zip | ||
| 文件大小 | 53.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-11-21 20:37:59 | ||
图片预览

文档简介
九年级综合实践课2 九年级数学备课组(主备人: )
《关于一次函数与反比例函数的交点》 第二课时
在数学学习中,经常会遇到一次函数与反比例函数的交点的问题。
研究2:一次函数与反比例函数的交点坐标的特点。
方程:的两个实数解(即两函数交点的横坐标)为:
与它们相对应的两个纵坐标为:。观察它们,不难发现:
点A和点B各自的横、纵坐标的积都等于反比例系数。
点A和点B的横坐标的和等于正比例函数的图像在x轴上的截距。
点A和点B的纵坐标的和等于正比例函数的图像在y轴上的截距。
当时,OA=OB
当时,点A的横坐标等于点B的纵坐标,点A的纵坐标等于点B的横坐标。
当时,点A的横坐标与点B的纵坐标互为相反数,点A的纵坐标与点B的横坐标互为相反数。
(当、异号时)
(当、同号时)
学以致用:
1.已知:在矩形中,,.分别以所在直线为轴和轴,建立如图所示的平面直角坐标系.是边上的一个动点(不与重合),过点的反比例函数的图象与边交于点.
(1)求证:与的面积相等;
(2)记,求当为何值时,有最大值,最大值为多少?
(3)请探索:是否存在这样的点,使得将沿对折后,点恰好落在上?若存在,求出点的坐标;若不存在,请说明理由.
解:(1)先设E点的坐标为(a,3);F点的坐标为(4,b)。因为它们都在同一个反比例函数图像上,所以有
(这里其实还有:,那么我又猜测:一次函数与反比例函数的两个交点的连线平行于这两个交点在坐标轴上的射影间的连线。这个猜测对不对呢?)
(2)∵
∴
说明了时,有最大值,最大值为3(很有意思的是,此时点E、F都在所在边的中点处)
(3)将沿对折后,点恰好落在上时,
易知△EDG∽△GBF。并且还知道相似比:
而:OD=
∴点F的坐标为(4,)
巩固练习:
1.如图所示,Rt△ABO的顶点A是双曲线y=与直线y=-x-(k+1)在第二象限的交点,AB⊥x轴于B,且S△ABO=.
(1)求这两个函数的解析式;
(2)求直线与双曲线的两个交点A、C的坐标和△AOC的面积.
课后反思:
《关于一次函数与反比例函数的交点》 第二课时
在数学学习中,经常会遇到一次函数与反比例函数的交点的问题。
研究2:一次函数与反比例函数的交点坐标的特点。
方程:的两个实数解(即两函数交点的横坐标)为:
与它们相对应的两个纵坐标为:。观察它们,不难发现:
点A和点B各自的横、纵坐标的积都等于反比例系数。
点A和点B的横坐标的和等于正比例函数的图像在x轴上的截距。
点A和点B的纵坐标的和等于正比例函数的图像在y轴上的截距。
当时,OA=OB
当时,点A的横坐标等于点B的纵坐标,点A的纵坐标等于点B的横坐标。
当时,点A的横坐标与点B的纵坐标互为相反数,点A的纵坐标与点B的横坐标互为相反数。
(当、异号时)
(当、同号时)
学以致用:
1.已知:在矩形中,,.分别以所在直线为轴和轴,建立如图所示的平面直角坐标系.是边上的一个动点(不与重合),过点的反比例函数的图象与边交于点.
(1)求证:与的面积相等;
(2)记,求当为何值时,有最大值,最大值为多少?
(3)请探索:是否存在这样的点,使得将沿对折后,点恰好落在上?若存在,求出点的坐标;若不存在,请说明理由.
解:(1)先设E点的坐标为(a,3);F点的坐标为(4,b)。因为它们都在同一个反比例函数图像上,所以有
(这里其实还有:,那么我又猜测:一次函数与反比例函数的两个交点的连线平行于这两个交点在坐标轴上的射影间的连线。这个猜测对不对呢?)
(2)∵
∴
说明了时,有最大值,最大值为3(很有意思的是,此时点E、F都在所在边的中点处)
(3)将沿对折后,点恰好落在上时,
易知△EDG∽△GBF。并且还知道相似比:
而:OD=
∴点F的坐标为(4,)
巩固练习:
1.如图所示,Rt△ABO的顶点A是双曲线y=与直线y=-x-(k+1)在第二象限的交点,AB⊥x轴于B,且S△ABO=.
(1)求这两个函数的解析式;
(2)求直线与双曲线的两个交点A、C的坐标和△AOC的面积.
课后反思:
同课章节目录
