华东师大版九年级数学下册 26.2.2 y=a(x-h)2 课件(16张)
文档属性
| 名称 | 华东师大版九年级数学下册 26.2.2 y=a(x-h)2 课件(16张) |
|
|
| 格式 | ppt | ||
| 文件大小 | 353.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-02 00:00:00 | ||
图片预览




文档简介
y=ax2+k
a>0
a<0
图象
开口
对称性
顶点
增减性
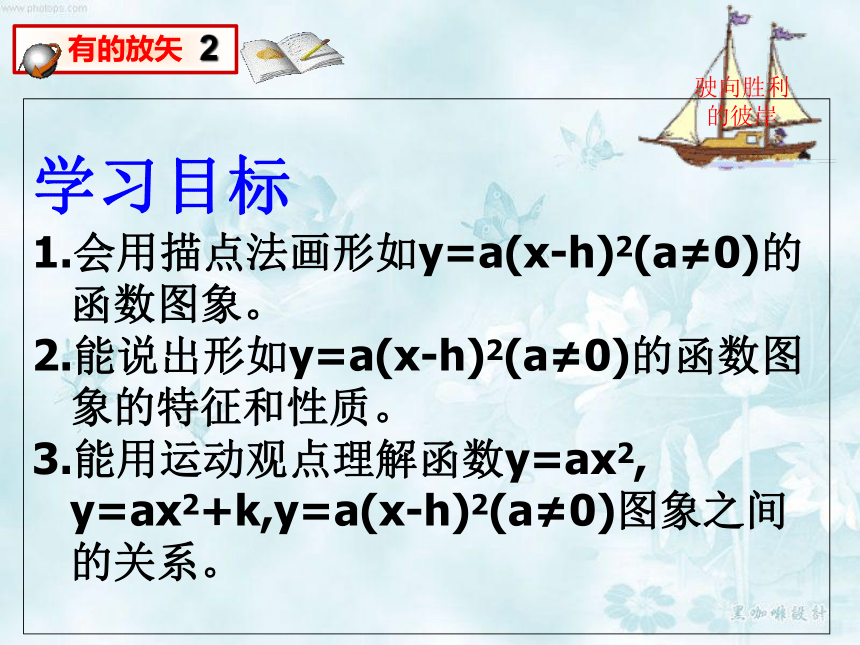
二次函数y=ax2+k的性质
开口向上
开口向下
a的绝对值越大,开口越小
关于y轴对称
当x=0时y最小,y=k
当x=0时y最大,y=k
在对称轴左侧递减
在对称轴右侧递增
在对称轴左侧递增
在对称轴右侧递减
k>0
k<0
k<0
k>0
(0,k)
二次函数y=a(x-h)2 的图象和性质
有的放矢
2
驶向胜利的彼岸
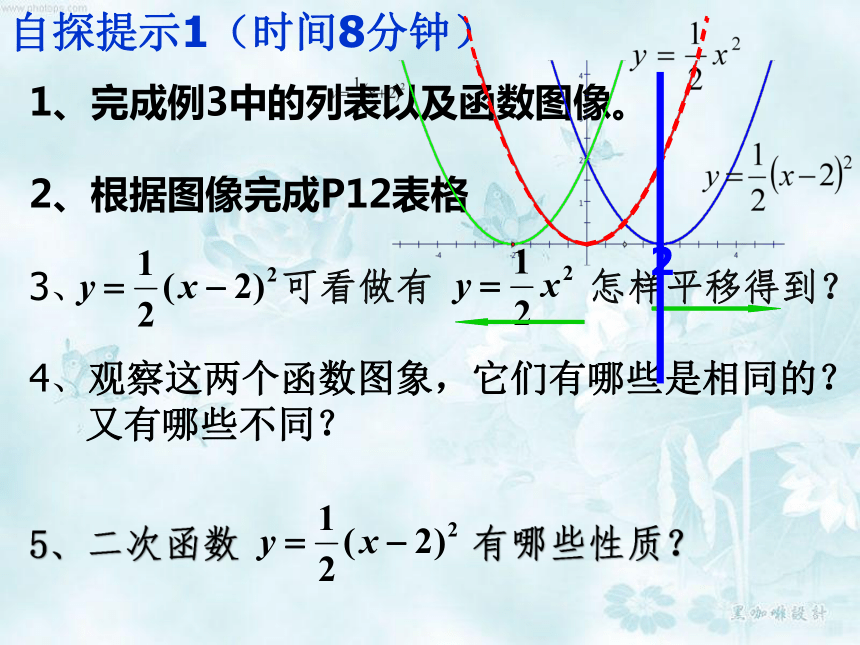
学习目标
1.会用描点法画形如y=a(x-h)2(a≠0)的
函数图象。
2.能说出形如y=a(x-h)2(a≠0)的函数图
象的特征和性质。
3.能用运动观点理解函数y=ax2,
y=ax2+k,y=a(x-h)2(a≠0)图象之间
的关系。
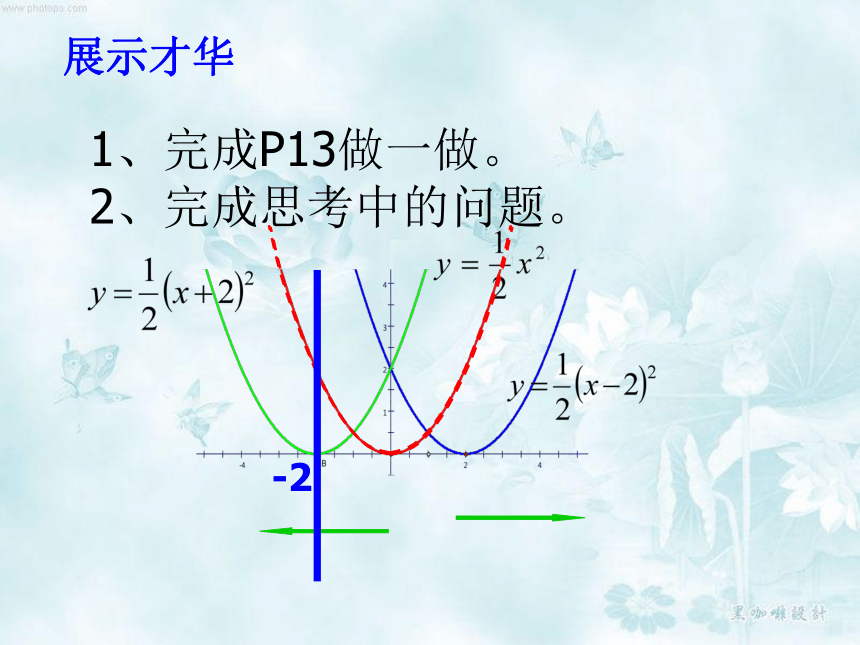
自探提示1(时间8分钟)
1、完成例3中的列表以及函数图像。
2、根据图像完成P12表格
3、 可看做有 怎样平移得到?
4、观察这两个函数图象,它们有哪些是相同的?
又有哪些不同?
5、二次函数 有哪些性质?
2
展示才华
1、完成P13做一做。
2、完成思考中的问题。
-2
小试牛刀
当x为何值时,y随x的增大而增大?
1、说出下列抛物线的开口方向、
对称轴:
顶点坐标和
(1)
(2)
(3)
(5)
(4)
试一试
1. 填空题
(1)二次函数y=2(x+5)2的图像是 ,开口 ,对称轴是 ,当x= 时,y有最 值,是 .
(2)二次函数y=-3(x-4)2的图像是由抛物线y= -3x2 向 平移 个单位得到的;开口 ,对称轴是 ,当x= 时,y有最 值,是 .
抛物线
向上
直线x= -5
-5
小
0
右
4
向下
直线x= 4
4
大
0
(3)将二次函数y=2x2的图像向右平移3个单位后得到函数 的图像,其对称轴是 ,顶点是 ,当x 时,y随x的增大而增大;当x _________时 ,y随x的增大而减小. (4)将二次函数y= -3(x-2)2的图像向左平移3个单位后得到函数 的图像,其顶点坐标是 ,对称轴是 ,当x= 时,y有最 值,是 .
y=2(x-3)2
直线x=3
(3,0)
>3
<3
y= -3(x+1)2
(-1,0)
直线x=-1
-1
大
0
(5)抛物线y=4(x-3)2的开口方向 ,对称轴是 ,顶点坐标是 ,抛物线有最 点,
当x= 时,y有最 值,其值为 。
抛物线与x轴交点坐标 ,与y轴交点坐标 。
向上
直线x=3
(3,0)
低
3
小
0
(3,0)
(0,36)
大显身手
抛物线
开口方向
对称轴
顶点坐标
y = 2(x+3)2
y = -3(x-1)2
y = -4(x-3)2
向上
直线x=-3
( -3 , 0 )
直线x=1
直线x=3
向下
向下
( 1 , 0 )
( 3, 0)
1.不画图直接填空
2.形状与y=-2(x+3)2的图象形状相同,但开口方向不同,顶点坐标是(1,0)的抛物线解析式。
4、把抛物线
向左平
移 3 个单位,
可得到抛物
线 .
右
4
Y=2(x+3)2
Y=2(x-4)2
5、把抛物线
向 平
移 个单位,
可得到抛物线
右
1
左
3
6、把抛物线
向 平
移 个单位,
可得到抛物线
2
左
右
5
7、把抛物线
向 平
移 个单位,
可得到抛物线
右
3
左
1
回味无穷
谈谈这节课你收获了什么?
小 结
驶向胜利的彼岸
小结
3.抛物线y=ax2+k有如下特点:
当a>0时, 开口向上;
当a<0时,开口向下.
(2)对称轴是y轴;
(3)顶点是(0,k).
抛物线y=a(x-h)2有如下特点:
(1)当a>0时, 开口向上,当a<0时,开口向下;
(2)对称轴是直线x=h;
(3)顶点是(h,0).
2.抛物线y=ax2+k可以由抛物线y=ax2向上或向下平移|k|得到.
抛物线y=a(x-h)2可以由抛物线y=ax2向左或向右平移|h|得到.
(k>0,向上平移;k<0向下平移.)
(h>0,向右平移;h<0向左平移.)
1.抛物线y=ax2+k、抛物线y=a(x-h)2和抛物线y=ax2的形状完全相同,开口方向一致;
(1)当a>0时, 开口向上,当a<0时,开口向下;
知识的升华
独立
作业
祝你成功!
驶向胜利的彼岸
课后练习1、2、3、
学习指导练习四
a>0
a<0
图象
开口
对称性
顶点
增减性
二次函数y=ax2+k的性质
开口向上
开口向下
a的绝对值越大,开口越小
关于y轴对称
当x=0时y最小,y=k
当x=0时y最大,y=k
在对称轴左侧递减
在对称轴右侧递增
在对称轴左侧递增
在对称轴右侧递减
k>0
k<0
k<0
k>0
(0,k)
二次函数y=a(x-h)2 的图象和性质
有的放矢
2
驶向胜利的彼岸
学习目标
1.会用描点法画形如y=a(x-h)2(a≠0)的
函数图象。
2.能说出形如y=a(x-h)2(a≠0)的函数图
象的特征和性质。
3.能用运动观点理解函数y=ax2,
y=ax2+k,y=a(x-h)2(a≠0)图象之间
的关系。
自探提示1(时间8分钟)
1、完成例3中的列表以及函数图像。
2、根据图像完成P12表格
3、 可看做有 怎样平移得到?
4、观察这两个函数图象,它们有哪些是相同的?
又有哪些不同?
5、二次函数 有哪些性质?
2
展示才华
1、完成P13做一做。
2、完成思考中的问题。
-2
小试牛刀
当x为何值时,y随x的增大而增大?
1、说出下列抛物线的开口方向、
对称轴:
顶点坐标和
(1)
(2)
(3)
(5)
(4)
试一试
1. 填空题
(1)二次函数y=2(x+5)2的图像是 ,开口 ,对称轴是 ,当x= 时,y有最 值,是 .
(2)二次函数y=-3(x-4)2的图像是由抛物线y= -3x2 向 平移 个单位得到的;开口 ,对称轴是 ,当x= 时,y有最 值,是 .
抛物线
向上
直线x= -5
-5
小
0
右
4
向下
直线x= 4
4
大
0
(3)将二次函数y=2x2的图像向右平移3个单位后得到函数 的图像,其对称轴是 ,顶点是 ,当x 时,y随x的增大而增大;当x _________时 ,y随x的增大而减小. (4)将二次函数y= -3(x-2)2的图像向左平移3个单位后得到函数 的图像,其顶点坐标是 ,对称轴是 ,当x= 时,y有最 值,是 .
y=2(x-3)2
直线x=3
(3,0)
>3
<3
y= -3(x+1)2
(-1,0)
直线x=-1
-1
大
0
(5)抛物线y=4(x-3)2的开口方向 ,对称轴是 ,顶点坐标是 ,抛物线有最 点,
当x= 时,y有最 值,其值为 。
抛物线与x轴交点坐标 ,与y轴交点坐标 。
向上
直线x=3
(3,0)
低
3
小
0
(3,0)
(0,36)
大显身手
抛物线
开口方向
对称轴
顶点坐标
y = 2(x+3)2
y = -3(x-1)2
y = -4(x-3)2
向上
直线x=-3
( -3 , 0 )
直线x=1
直线x=3
向下
向下
( 1 , 0 )
( 3, 0)
1.不画图直接填空
2.形状与y=-2(x+3)2的图象形状相同,但开口方向不同,顶点坐标是(1,0)的抛物线解析式。
4、把抛物线
向左平
移 3 个单位,
可得到抛物
线 .
右
4
Y=2(x+3)2
Y=2(x-4)2
5、把抛物线
向 平
移 个单位,
可得到抛物线
右
1
左
3
6、把抛物线
向 平
移 个单位,
可得到抛物线
2
左
右
5
7、把抛物线
向 平
移 个单位,
可得到抛物线
右
3
左
1
回味无穷
谈谈这节课你收获了什么?
小 结
驶向胜利的彼岸
小结
3.抛物线y=ax2+k有如下特点:
当a>0时, 开口向上;
当a<0时,开口向下.
(2)对称轴是y轴;
(3)顶点是(0,k).
抛物线y=a(x-h)2有如下特点:
(1)当a>0时, 开口向上,当a<0时,开口向下;
(2)对称轴是直线x=h;
(3)顶点是(h,0).
2.抛物线y=ax2+k可以由抛物线y=ax2向上或向下平移|k|得到.
抛物线y=a(x-h)2可以由抛物线y=ax2向左或向右平移|h|得到.
(k>0,向上平移;k<0向下平移.)
(h>0,向右平移;h<0向左平移.)
1.抛物线y=ax2+k、抛物线y=a(x-h)2和抛物线y=ax2的形状完全相同,开口方向一致;
(1)当a>0时, 开口向上,当a<0时,开口向下;
知识的升华
独立
作业
祝你成功!
驶向胜利的彼岸
课后练习1、2、3、
学习指导练习四
