浙教版八年级数学上册1.3证明(2)教案
文档属性
| 名称 | 浙教版八年级数学上册1.3证明(2)教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 183.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-03 10:50:43 | ||
图片预览



文档简介
浙教版数学八年级下1.3证明(2)教学设计
课题
证明(2)
单元
第
一章
学科
数学
年级
八年级
学习目标
情感态度和价值观目标
学生在学完证明之后,能够对数学的逻辑推理严密思维有一定的体验和感受,并利用这种思维解决更多的问题。
能力目标
通过简单命题的证明,训练学生的逻辑推理能力和自主探究能力
知识目标
1.进一步理解证明的含义2.探索并理解三角形内角和定理的几何证明3.三角形外角的性质
重点
探索三角形内角和定理的证明
难点
复杂命题的证明,多个定理的运用
学法
自主探究
教法
讲授法、引导法
教学过程
教学环节
教师活动
学生活动
设计意图
回忆旧知
上节课我们学习了证明的概念,以及平行线性质的相关证明题。下面来做题巩固练习。1.如图,已知AE∥BC,AE平分∠DAC.求证:AB=AC.证明:∵AE平分∠DAC,∴∠1=∠2。(角平分线的定义)
∵AE∥BC,∴∠1=∠B,(两直线平行,同位角相等)∠2=∠C。(两直线平行,内错角相等)
∴∠B=∠C。∴AB=AC。(等角对等边)2.证明“直角三角形斜边上的中线等于斜边的一半”是真命题。思考:这一题与上一题最大的不同在哪里?上一题已知和求证是给出的,这一题需要将文字转化为数学语言。
回忆旧知,做练习
引导学生回忆所学,通过对比引出新知
讲授新课
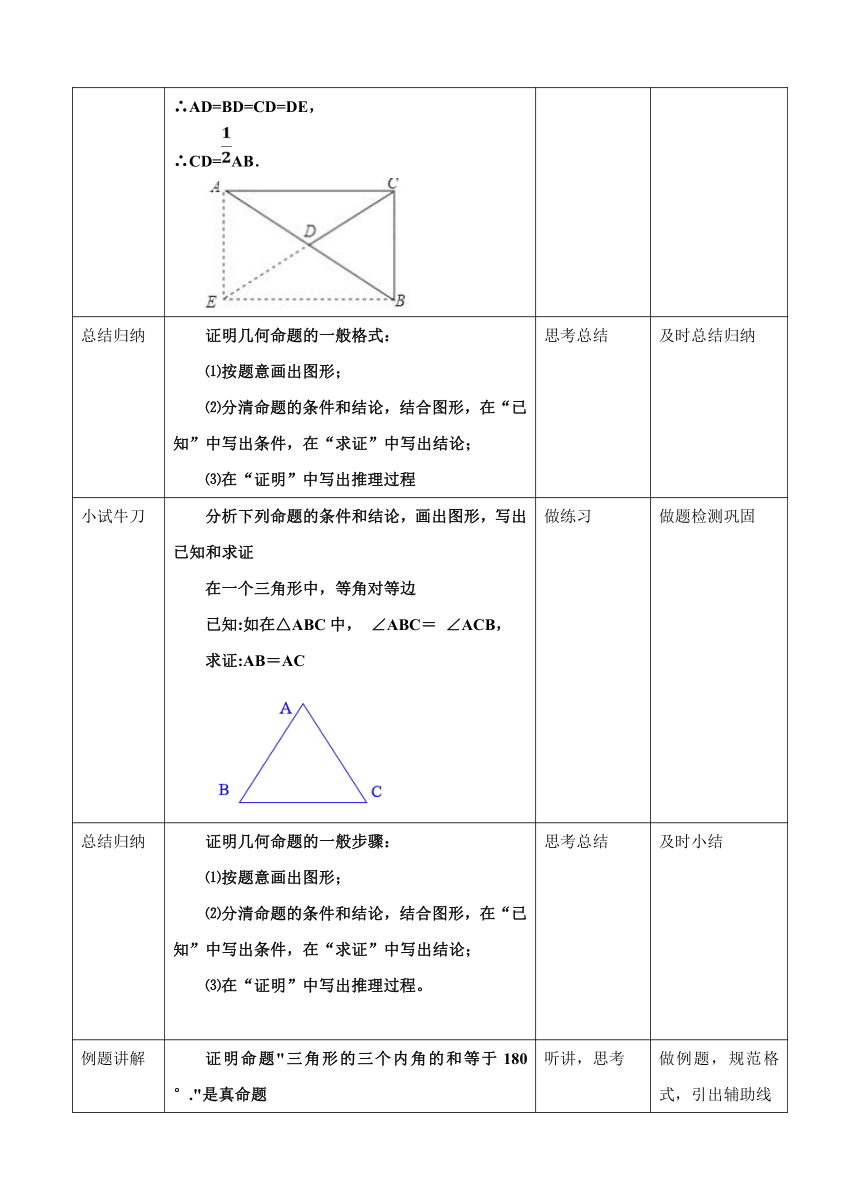
画:根据题意,画出图形写:找出命题的条件和结论。“已知”----条件,“求证”----结论.已知:如图,在△ABC中,∠ACB=90°,CD是斜边AB上的中线求证:
CD=AB.证:在“证明”中写出推理过程证明:如图,延长CD到E,使DE=CD,连接AE、BE,
∵CD是斜边AB上的中线,
∴AD=BD,
∴四边形AEBC是平行四边形,
∵∠ACB=90°,
∴四边形AEBC是矩形,
∴AD=BD=CD=DE,
∴CD=AB.
思考回答问题
通过做题来归纳证明的步骤
总结归纳
证明几何命题的一般格式:⑴按题意画出图形;⑵分清命题的条件和结论,结合图形,在“已知”中写出条件,在“求证”中写出结论;⑶在“证明”中写出推理过程
思考总结
及时总结归纳
小试牛刀
分析下列命题的条件和结论,画出图形,写出已知和求证在一个三角形中,等角对等边已知:如在△ABC中,
∠ABC=
∠ACB,求证:AB=AC
做练习
做题检测巩固
总结归纳
证明几何命题的一般步骤:⑴按题意画出图形;⑵分清命题的条件和结论,结合图形,在“已知”中写出条件,在“求证”中写出结论;⑶在“证明”中写出推理过程。
思考总结
及时小结
例题讲解
证明命题"三角形的三个内角的和等于180°."是真命题已知:∠A
,
∠B,
∠C是三角形的三个内角求证:
∠A
+∠B+
∠C=180°证明:过A
作
AE
//
BC则∠C=∠2,∠B=∠1(两直线平行,内错角相等)∴∠BAC+∠B+∠C=∠BAC+∠1+∠2=∠DAE=180?(平角的定义)在解决几何问题时,有时需要添加辅助线,添辅助线的过程要写入证明中,
辅助线通常画成虚线。你还有其他证明方法吗?证法2:作BC的延长线CD,过点C作射线CE//AB,则∠1=∠A(两直线平行,内错角相等)∠2=∠B(两直线平行,同位角相等)∵∠1+∠2+∠ACB=180°∴∠A+∠B+∠ACB=180°证法3:证明:在BC上任取一点D,过D作DE//AB,作DF//AC。∴∠1=∠B,∠2=∠C,∠DEC=∠A,
∵DE∥AB,∴∠3=∠DEC,
∴∠3=∠A,
∵∠1+∠2+∠3=180°∴∠A+∠B+∠C=180°
听讲,思考
做例题,规范格式,引出辅助线
总结归纳
1.辅助线是为了证明需要在原图上添画的线.(辅助线通常画成虚线)2.它的作用是把分散的条件集中,把隐含的条件显现出来,起到牵线搭桥的作用.3.添加辅助线,可构造新图形,形成新关系,找到联系已知与未知的桥梁,把问题转化,但辅助线的添法没有一定的规律,要根据需要而定,平时做题时要注意总结.
总结思考
让学生明白辅助线的作用以及添加方式
讲授新知
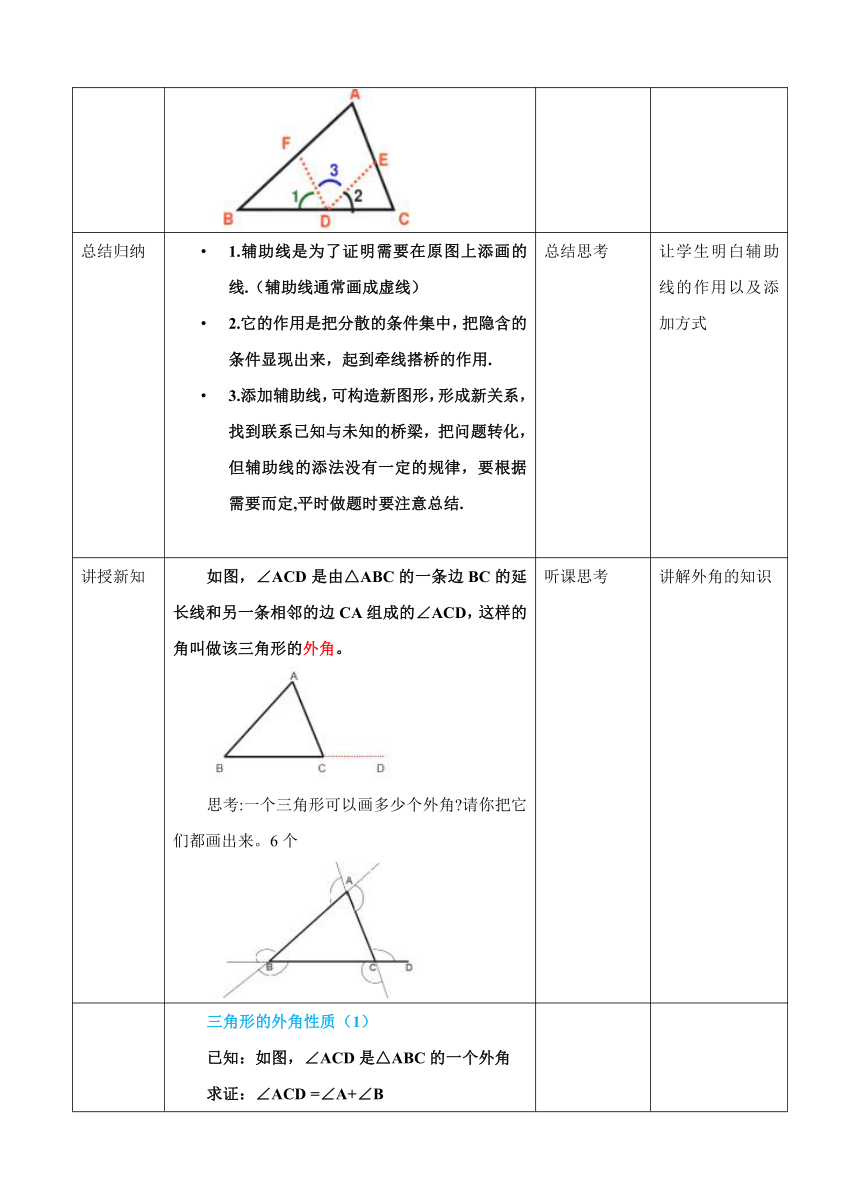
如图,∠ACD是由△ABC的一条边BC的延长线和另一条相邻的边CA组成的∠ACD,这样的角叫做该三角形的外角。思考:一个三角形可以画多少个外角?请你把它们都画出来。6个
听课思考
讲解外角的知识
三角形的外角性质(1)已知:如图,∠ACD是△ABC的一个外角求证:∠ACD
=∠A+∠B证明:∵∠ACD+∠ACB=180°∠A+∠B+∠ACB=180°∴∠ACD
=∠A+∠B三角形的一个外角等于与它不相邻的两个内角的和.三角形的外角性质(2)已知:如图,∠ACD是△ABC的一个外角求证:∠ACD
>∠A
∠ACD
>∠B证明:∵∠ACD
=∠A+∠B∴∠ACD
>∠A∠ACD
>∠B三角形的一个外角大于任何一个和它不相邻的内角.三角形的外角性质(3)已知:∠1、∠2、∠3为△ABC的三个外角,如图.
求证:∠1+∠2+∠3=360°.证明:∵∠1是△ABC的外角,∴∠1=∠ABC+∠ACB,
同理得∠2=∠ABC+∠BAC,∠3=∠ACB+∠BAC,
∴∠1+∠2+∠3=(∠ABC+∠ACB)+(∠ABC+∠BAC)+(∠ACB+∠BAC)=2(∠ABC+∠ACB+∠BAC)
∵∠ABC+∠ACB+∠BAC=180°,
∴∠1+∠2+∠3=360°.三角形的外角和为360°.
例题讲解
已知:如图,∠B+
∠D=∠BCD,求证:
AB//
DE证明:如图,延长BC,交DE于点F。∵
∠B+
∠D=
∠BCD(已知)又∵
∠BCD=
∠D+
∠CFD(三角形的外角等于和它不相邻的两个内角的和),∴
∠B+
∠D=
∠D+
∠CFD∴
∠B=
∠CFD∴AB∥DE(内错角相等,两直线平行)方法2:证明:过点C做直线CF使得CF//AB
(F在C的右侧)
∵
CF//AB
∴∠B=∠BCF
(两直线平行,内错角相等)
∵∠BCD=∠B+∠D
(已知)
且∠BCD=∠BCF+∠DCF
(如图)
∴∠B+∠D=∠BCF+∠DCF=∠B+∠DCF
(等量代换)
即∠D=∠DCF
∴CF//ED
(内错角相等,两直线平行)
∴AB//ED
(两条直线分别平行于第三条直线,两直线平行)
做题
做例题,强化应用
达标测评
1.已知,如图,在
△
ABC中,AB=2AC求证:AC<BC<3AC。证明:∵AB=2AC,AC+BC>AB
∴AC3AC=AC+AB
∵BC∴AC2.如图,P为⊿ABC内任意的一点,∠1=∠2。求证:∠ACB与∠BPC互补证明:
∵∠ACB=∠1+∠BCP,∠1=∠2
∴∠ACB=∠2+∠BCP
∵∠2+∠BCP+∠BPC=180
∴∠ACB+∠BPC=180
∴∠ACB与∠BPC互补3.课本中对菱形的另外一个性质“菱形的对角线平分一组对角”却没有给出判定定理,请你利用如图所示图形研究一下这个问题.
要求:如果有类似的判定定理,请写出已知、求证并证明.如果没有,请举出反例.答:有判定定理。已知:在平行四边形ABCD中,对角线AC平分∠DAB和∠DCB求证:四边形ABCD是菱形。∴AD=DC∴四边形ABCD是菱形
做题
检测学习情况
应用提高
1.如图,在五角星图形中,求:∠A+
∠B+
∠C+
∠D+
∠E的度数。解:如右图所示,
∵∠1=∠C+∠2,∠2=∠A+∠D,
∴∠1=∠C+∠A+∠D,
又∵∠1+∠B+∠E=180°,
∴∠A+∠B+∠C+∠D+∠E=180°.
故答案是:180°.2.如图,在△ABC中,∠C>∠A,BD为角平分线,BE⊥AC,垂足为E.若∠DBE=10°,则∠C-∠A的度数为____20°__.解:∵BD为角平分线,
∴∠ABD=∠DBC,
∵BE⊥AC,
∴在△BCE中,∠CBE=90°-∠C,
∵∠DBE=10°,
∴∠DBC=∠CBE+∠DBE=90°-∠C+10°,
在△ABD中,∠BDE=∠A+∠ABD=∠A+90°-∠C+10°=∠A-∠C+100°,
在Rt△BDE中,∠BDE+∠DBE=90°,
∴∠A-∠C+100°+10°=90°,
整理得,∠C-∠A=20
做题
拓展提升
课堂小结
这节课我们学习了:1.证明的步骤2.三角形内角和定理3.三角形外角定理
回忆总结
总结本节课所学知识
课后作业
课本P页第20页1、4
题
练习
课后做题巩固
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
课题
证明(2)
单元
第
一章
学科
数学
年级
八年级
学习目标
情感态度和价值观目标
学生在学完证明之后,能够对数学的逻辑推理严密思维有一定的体验和感受,并利用这种思维解决更多的问题。
能力目标
通过简单命题的证明,训练学生的逻辑推理能力和自主探究能力
知识目标
1.进一步理解证明的含义2.探索并理解三角形内角和定理的几何证明3.三角形外角的性质
重点
探索三角形内角和定理的证明
难点
复杂命题的证明,多个定理的运用
学法
自主探究
教法
讲授法、引导法
教学过程
教学环节
教师活动
学生活动
设计意图
回忆旧知
上节课我们学习了证明的概念,以及平行线性质的相关证明题。下面来做题巩固练习。1.如图,已知AE∥BC,AE平分∠DAC.求证:AB=AC.证明:∵AE平分∠DAC,∴∠1=∠2。(角平分线的定义)
∵AE∥BC,∴∠1=∠B,(两直线平行,同位角相等)∠2=∠C。(两直线平行,内错角相等)
∴∠B=∠C。∴AB=AC。(等角对等边)2.证明“直角三角形斜边上的中线等于斜边的一半”是真命题。思考:这一题与上一题最大的不同在哪里?上一题已知和求证是给出的,这一题需要将文字转化为数学语言。
回忆旧知,做练习
引导学生回忆所学,通过对比引出新知
讲授新课
画:根据题意,画出图形写:找出命题的条件和结论。“已知”----条件,“求证”----结论.已知:如图,在△ABC中,∠ACB=90°,CD是斜边AB上的中线求证:
CD=AB.证:在“证明”中写出推理过程证明:如图,延长CD到E,使DE=CD,连接AE、BE,
∵CD是斜边AB上的中线,
∴AD=BD,
∴四边形AEBC是平行四边形,
∵∠ACB=90°,
∴四边形AEBC是矩形,
∴AD=BD=CD=DE,
∴CD=AB.
思考回答问题
通过做题来归纳证明的步骤
总结归纳
证明几何命题的一般格式:⑴按题意画出图形;⑵分清命题的条件和结论,结合图形,在“已知”中写出条件,在“求证”中写出结论;⑶在“证明”中写出推理过程
思考总结
及时总结归纳
小试牛刀
分析下列命题的条件和结论,画出图形,写出已知和求证在一个三角形中,等角对等边已知:如在△ABC中,
∠ABC=
∠ACB,求证:AB=AC
做练习
做题检测巩固
总结归纳
证明几何命题的一般步骤:⑴按题意画出图形;⑵分清命题的条件和结论,结合图形,在“已知”中写出条件,在“求证”中写出结论;⑶在“证明”中写出推理过程。
思考总结
及时小结
例题讲解
证明命题"三角形的三个内角的和等于180°."是真命题已知:∠A
,
∠B,
∠C是三角形的三个内角求证:
∠A
+∠B+
∠C=180°证明:过A
作
AE
//
BC则∠C=∠2,∠B=∠1(两直线平行,内错角相等)∴∠BAC+∠B+∠C=∠BAC+∠1+∠2=∠DAE=180?(平角的定义)在解决几何问题时,有时需要添加辅助线,添辅助线的过程要写入证明中,
辅助线通常画成虚线。你还有其他证明方法吗?证法2:作BC的延长线CD,过点C作射线CE//AB,则∠1=∠A(两直线平行,内错角相等)∠2=∠B(两直线平行,同位角相等)∵∠1+∠2+∠ACB=180°∴∠A+∠B+∠ACB=180°证法3:证明:在BC上任取一点D,过D作DE//AB,作DF//AC。∴∠1=∠B,∠2=∠C,∠DEC=∠A,
∵DE∥AB,∴∠3=∠DEC,
∴∠3=∠A,
∵∠1+∠2+∠3=180°∴∠A+∠B+∠C=180°
听讲,思考
做例题,规范格式,引出辅助线
总结归纳
1.辅助线是为了证明需要在原图上添画的线.(辅助线通常画成虚线)2.它的作用是把分散的条件集中,把隐含的条件显现出来,起到牵线搭桥的作用.3.添加辅助线,可构造新图形,形成新关系,找到联系已知与未知的桥梁,把问题转化,但辅助线的添法没有一定的规律,要根据需要而定,平时做题时要注意总结.
总结思考
让学生明白辅助线的作用以及添加方式
讲授新知
如图,∠ACD是由△ABC的一条边BC的延长线和另一条相邻的边CA组成的∠ACD,这样的角叫做该三角形的外角。思考:一个三角形可以画多少个外角?请你把它们都画出来。6个
听课思考
讲解外角的知识
三角形的外角性质(1)已知:如图,∠ACD是△ABC的一个外角求证:∠ACD
=∠A+∠B证明:∵∠ACD+∠ACB=180°∠A+∠B+∠ACB=180°∴∠ACD
=∠A+∠B三角形的一个外角等于与它不相邻的两个内角的和.三角形的外角性质(2)已知:如图,∠ACD是△ABC的一个外角求证:∠ACD
>∠A
∠ACD
>∠B证明:∵∠ACD
=∠A+∠B∴∠ACD
>∠A∠ACD
>∠B三角形的一个外角大于任何一个和它不相邻的内角.三角形的外角性质(3)已知:∠1、∠2、∠3为△ABC的三个外角,如图.
求证:∠1+∠2+∠3=360°.证明:∵∠1是△ABC的外角,∴∠1=∠ABC+∠ACB,
同理得∠2=∠ABC+∠BAC,∠3=∠ACB+∠BAC,
∴∠1+∠2+∠3=(∠ABC+∠ACB)+(∠ABC+∠BAC)+(∠ACB+∠BAC)=2(∠ABC+∠ACB+∠BAC)
∵∠ABC+∠ACB+∠BAC=180°,
∴∠1+∠2+∠3=360°.三角形的外角和为360°.
例题讲解
已知:如图,∠B+
∠D=∠BCD,求证:
AB//
DE证明:如图,延长BC,交DE于点F。∵
∠B+
∠D=
∠BCD(已知)又∵
∠BCD=
∠D+
∠CFD(三角形的外角等于和它不相邻的两个内角的和),∴
∠B+
∠D=
∠D+
∠CFD∴
∠B=
∠CFD∴AB∥DE(内错角相等,两直线平行)方法2:证明:过点C做直线CF使得CF//AB
(F在C的右侧)
∵
CF//AB
∴∠B=∠BCF
(两直线平行,内错角相等)
∵∠BCD=∠B+∠D
(已知)
且∠BCD=∠BCF+∠DCF
(如图)
∴∠B+∠D=∠BCF+∠DCF=∠B+∠DCF
(等量代换)
即∠D=∠DCF
∴CF//ED
(内错角相等,两直线平行)
∴AB//ED
(两条直线分别平行于第三条直线,两直线平行)
做题
做例题,强化应用
达标测评
1.已知,如图,在
△
ABC中,AB=2AC求证:AC<BC<3AC。证明:∵AB=2AC,AC+BC>AB
∴AC
∵BC
∵∠ACB=∠1+∠BCP,∠1=∠2
∴∠ACB=∠2+∠BCP
∵∠2+∠BCP+∠BPC=180
∴∠ACB+∠BPC=180
∴∠ACB与∠BPC互补3.课本中对菱形的另外一个性质“菱形的对角线平分一组对角”却没有给出判定定理,请你利用如图所示图形研究一下这个问题.
要求:如果有类似的判定定理,请写出已知、求证并证明.如果没有,请举出反例.答:有判定定理。已知:在平行四边形ABCD中,对角线AC平分∠DAB和∠DCB求证:四边形ABCD是菱形。∴AD=DC∴四边形ABCD是菱形
做题
检测学习情况
应用提高
1.如图,在五角星图形中,求:∠A+
∠B+
∠C+
∠D+
∠E的度数。解:如右图所示,
∵∠1=∠C+∠2,∠2=∠A+∠D,
∴∠1=∠C+∠A+∠D,
又∵∠1+∠B+∠E=180°,
∴∠A+∠B+∠C+∠D+∠E=180°.
故答案是:180°.2.如图,在△ABC中,∠C>∠A,BD为角平分线,BE⊥AC,垂足为E.若∠DBE=10°,则∠C-∠A的度数为____20°__.解:∵BD为角平分线,
∴∠ABD=∠DBC,
∵BE⊥AC,
∴在△BCE中,∠CBE=90°-∠C,
∵∠DBE=10°,
∴∠DBC=∠CBE+∠DBE=90°-∠C+10°,
在△ABD中,∠BDE=∠A+∠ABD=∠A+90°-∠C+10°=∠A-∠C+100°,
在Rt△BDE中,∠BDE+∠DBE=90°,
∴∠A-∠C+100°+10°=90°,
整理得,∠C-∠A=20
做题
拓展提升
课堂小结
这节课我们学习了:1.证明的步骤2.三角形内角和定理3.三角形外角定理
回忆总结
总结本节课所学知识
课后作业
课本P页第20页1、4
题
练习
课后做题巩固
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
