圆中的有关计算
图片预览



文档简介
(共32张PPT)
与《圆》有关中的计算
长兴县泗安中学九年级备课组(cjc)
(建议两课时)
(一)圆中有关角的计算。
(一)基本要求
(三)圆中有关位置的计算。
(二)圆中有关线段的计算。
(四)圆中有关公式的计算。
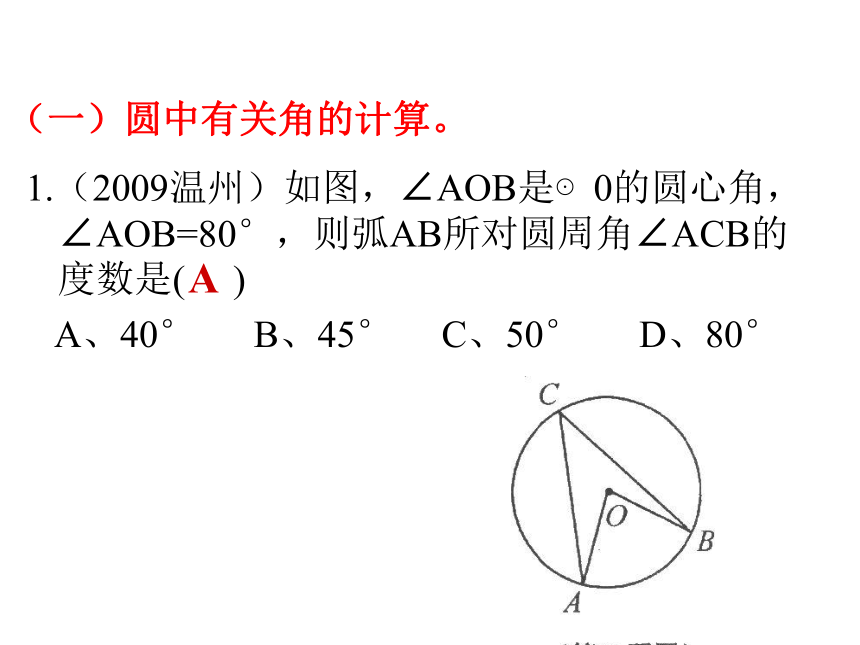
1.(2009温州)如图,∠AOB是⊙0的圆心角,∠AOB=80°,则弧AB所对圆周角∠ACB的度数是( )
A、40° B、45° C、50° D、80°
(一)圆中有关角的计算。
A
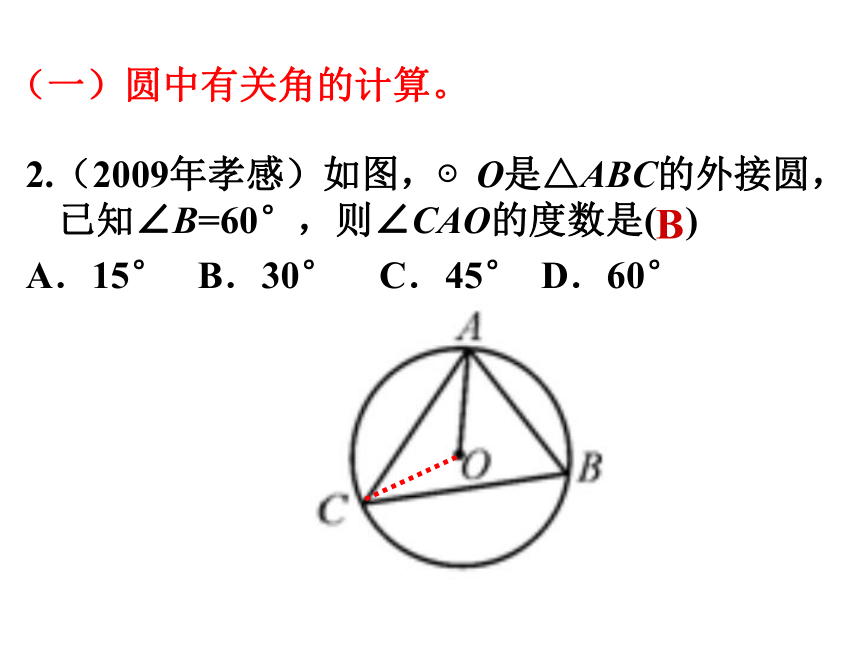
2.(2009年孝感)如图,⊙O是△ABC的外接圆,已知∠B=60°,则∠CAO的度数是( )
A.15° B.30° C.45° D.60°
(一)圆中有关角的计算。
B
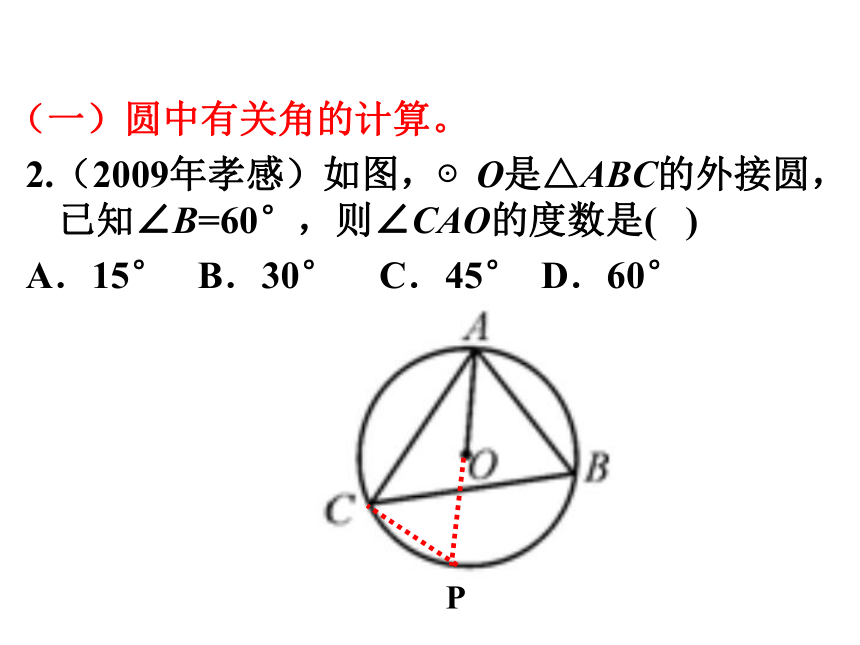
2.(2009年孝感)如图,⊙O是△ABC的外接圆,已知∠B=60°,则∠CAO的度数是( )
A.15° B.30° C.45° D.60°
(一)圆中有关角的计算。
P
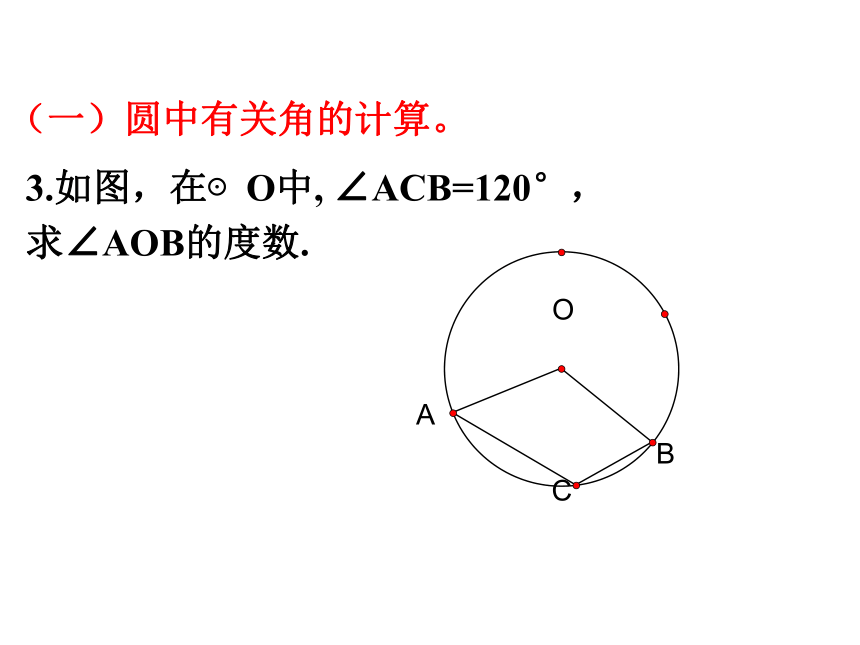
3.如图,在⊙O中, ∠ACB=120°,
求∠AOB的度数.
(一)圆中有关角的计算。
O
A
B
C
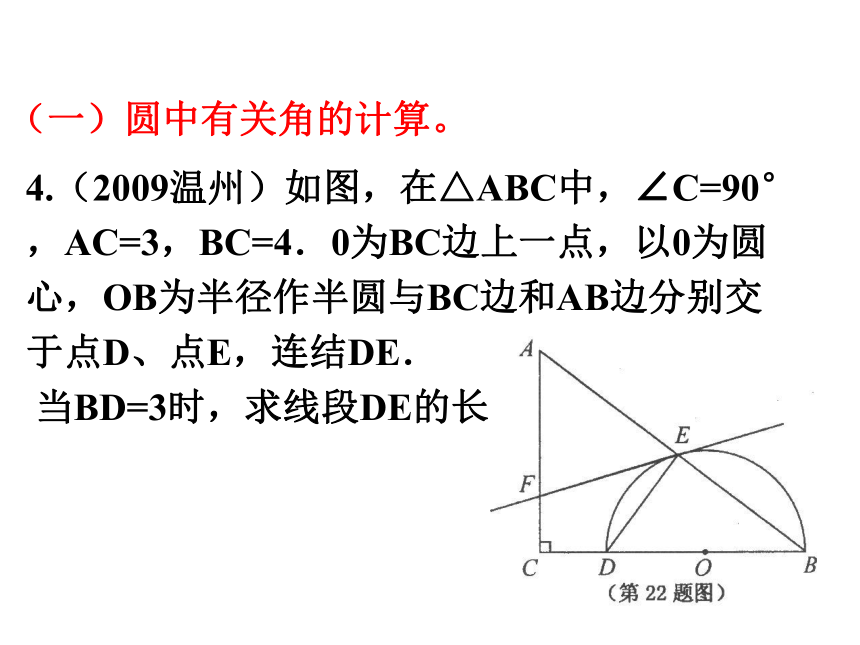
4.(2009温州)如图,在△ABC中,∠C=90°
,AC=3,BC=4.0为BC边上一点,以0为圆
心,OB为半径作半圆与BC边和AB边分别交
于点D、点E,连结DE.
当BD=3时,求线段DE的长;
(一)圆中有关角的计算。
(二)圆中有关线段的计算。
主要是圆的轴对称性的计算应用为主(专题复习)
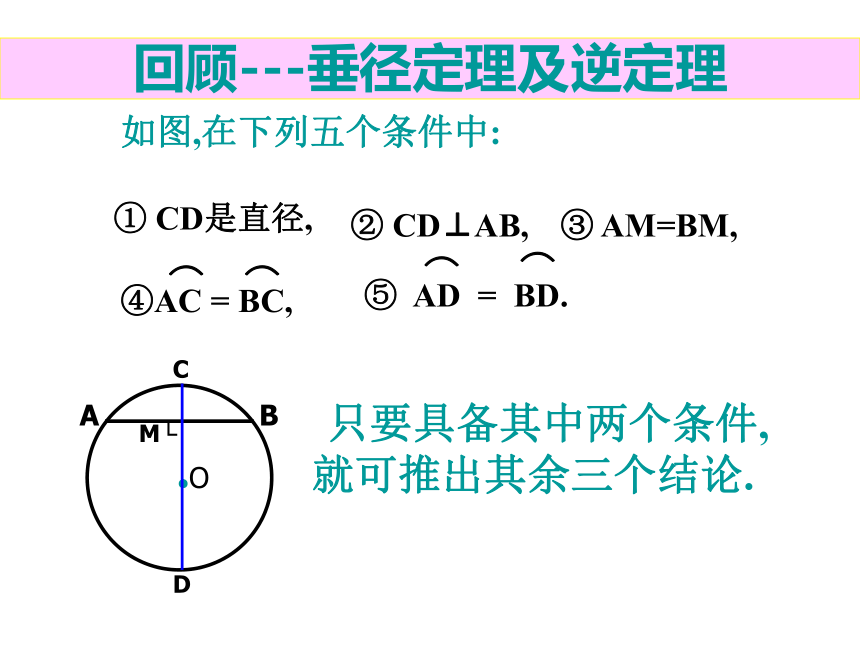
回顾---垂径定理及逆定理
如图,在下列五个条件中:
只要具备其中两个条件,就可推出其余三个结论.
●O
A
B
C
D
M└
① CD是直径,
③ AM=BM,
② CD⊥AB,
⌒
⌒
④AC = BC,
⌒
⌒
⑤ AD = BD.
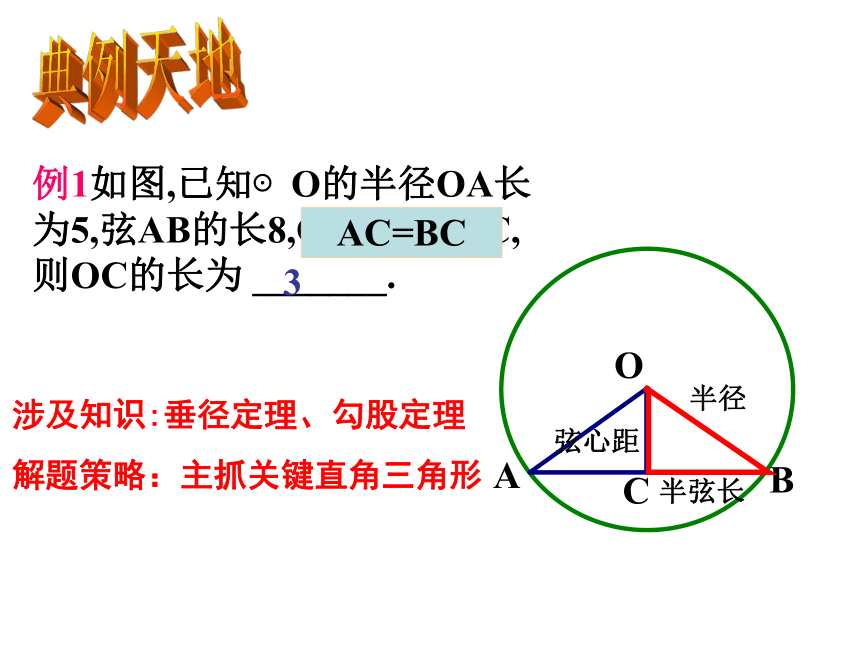
例1如图,已知⊙O的半径OA长为5,弦AB的长8,OC⊥AB于C,则OC的长为 _______.
O
A
B
C
3
AC=BC
弦心距
半径
半弦长
涉及知识:垂径定理、勾股定理
解题策略:主抓关键直角三角形
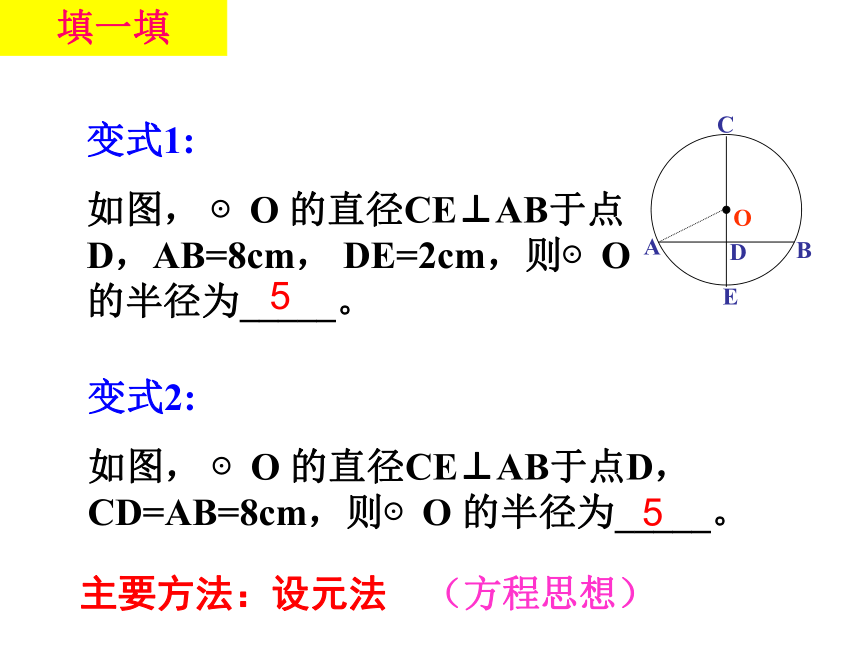
变式2:
如图, ⊙O 的直径CE⊥AB于点D,CD=AB=8cm,则⊙O 的半径为_____。
O
A
B
C
D
E
变式1:
如图, ⊙O 的直径CE⊥AB于点D,AB=8cm, DE=2cm,则⊙O 的半径为_____。
5
5
填一填
主要方法:设元法
(方程思想)
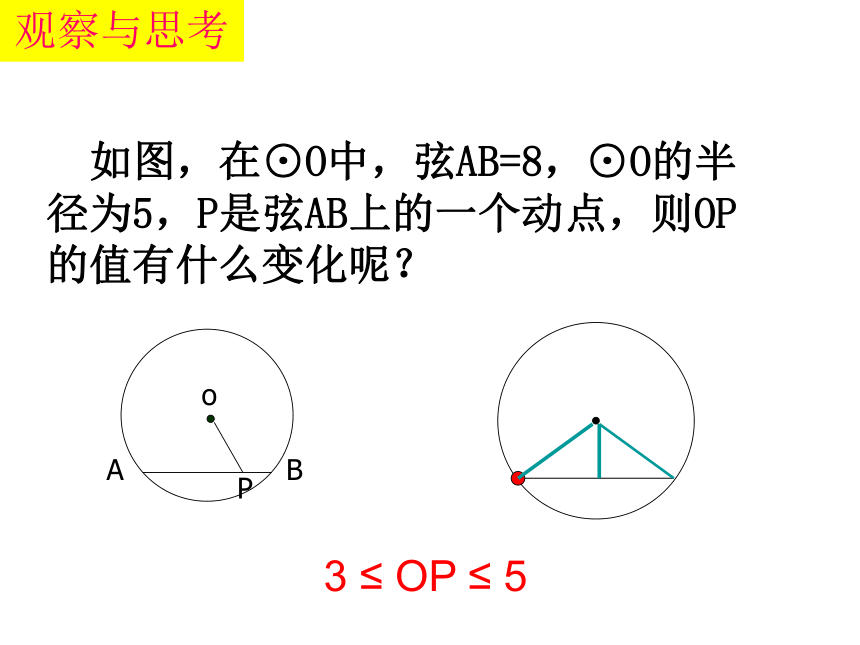
如图,在⊙O中,弦AB=8,⊙O的半径为5,P是弦AB上的一个动点,则OP的值有什么变化呢?
o
A
B
P
观察与思考
3 ≤ OP ≤ 5
变式1 过⊙O内一点D的最长弦长为10cm,最短弦长为8cm,那么OD长为( )
A.3 B.6cm C. cm D.9cm
A
O
A
B
C
D
E
画一画
最长的弦:过D点的直径
最短的弦:与过D点的直径相垂直的弦
已知⊙O的半径为10cm,点P是⊙O内一点,且OP=8,则过点P的所有弦中,最短的弦是( )
(A)6cm (B)8cm (C)10cm (D)12cm
D
10
8
6
变式2
变式3:已知⊙O的半径为5cm,点P是⊙O内一点,且OP=3cm,则过点P的所有弦中,弦长为整数的弦有几条
O
P
合作与探索
基本图形
(半径、半弦、弦心距构成的直角三角形)
1.如图,P为⊙O的弦BA延长线上一点,
PA=AB=2,PO=5,求⊙O的半径。
M
A
P
B
O
A
第一跳:
解题策略:作辅助线,借助两个直角三角形解决问题
如图所示,已知RtΔABC中,∠C=90°,AC= ,BC=1,若以C为圆心,CB为半径的圆交AB于P,则AP= 。
D
第二跳:
第三跳:
已知等腰ΔABC内接于⊙O,半径为5cm,底边BC长6cm,则其底边上的高是 。
按图形分类
1cm或9cm
两种方法:设元法、 简化构图法
一项策略:辅助线构建直角三角形
三个思想:建模、分类思想、方程思想
小结“一二三”
1.(2009年湖州)已知 与 外切,它们半径分别为2和3,则圆心距 长是( )
A. =1 B. =5 C.1< <5D. >5
2.(2009年台州)大圆半径为6,小圆半径为3,两圆圆心距为10,则两圆位置关系为( )
A.外离 B.外切 C.相交 D.内含
(三)圆中有关位置的计算。
B
A
(三)圆中有关位置的计算。
3.(2009年绍兴)如图, 、 的半径分别为1cm,2cm,圆心距AB为5cm.如果 由图示位置沿直线AB向右平移3cm,则此时该圆与 的位置关系是_____________.
B
A
相交
(三)圆中有关位置的计算。
4.(2009年潍坊)已知圆O的半径为R,AB是圆O的直径,D是AB延长线上一点,DC是圆O的切线,C是切点,连结AC,若∠ACB=300,则BD的长为( )
A.2 B. C. D.
(四)圆中有关公式的计算。
1.(2009年咸宁市)为庆祝祖国六十华诞,某单位排练的节目需用到如图所示的扇形布扇,布扇完全打开后,外侧两竹条AB、AC夹角为1200,AB的长为30cm,贴布部分BD的长为20cm,则贴布部分的面积约为________.cm2( 取3)
(四)圆中有关公式的计算。
2.(2007年湖州)已知扇形OBC、OAD的半径之间的关系是OB= OA,则BC的长是AD长的( )
A、 倍 B、2倍 C、 倍 D、4倍
A
B
C
D
O
(四)圆中有关公式的计算。
3.(2009年丽水)已知圆锥的底面半径
为3,母线长为4,则它的侧面积是( )
A. B. C. D. 12
4.(2009年义乌)如图,圆锥的侧面积为
,底面半径为3,则圆锥
的高AO为__________.
(四)圆中有关公式的计算。
5.(2009年台州)如图,三角板中,∠ACB=900,∠B=300,BC =6.三角板绕直角顶点C逆时针旋转,当点A的对应点A/落在AB边的起始位置上时即停止转动,则点转过的路径长为 .
主要是一些渗透数学思想方法的综合题
(二)较高要求与适度拓展
1. (2009年湖州)如图,已知在 中, , ,分别以AC、BC为直径作半圆,面积分别记为S1、S2,,则S1 + S2 的值等于 .
(二)较高要求与适度拓展
C
A
B
S1
S2
本题看似不可能,但
可以利用转化思想巧妙
地结合勾股定理,求出
S1 + S2的值,但两个“一半”
很容易导致计算错误。又如:
(2009年嘉兴)如图,⊙P内含于⊙O,⊙O的弦切⊙P于点C,且 .若阴影部分的面积为 ,则弦AB的长为( )
A.3 B.4 C.6 D.9
(二)较高要求与适度拓展
H
本题看似不可能,但通过转化思想,由阴影部分面积求出两圆半径的平方差,再综合垂经定理、勾股定理、平行线和切线的性质等知识,求出弦的半长。
2.(2009年绍兴)如图,在平面直角坐标系中, 与X轴相切于原点O,平行于y轴的直线交 于M、N 两点.若点M坐标(2,-1),则点N的坐标是( )
A(2,-4) B(2,-4.5) C(2,-5) D(2,-5.5)
(二)较高要求与适度拓展
本题通过辅助性和切线性质,构造一个直角三角形,利用方程思想求出圆的半径,再结合垂经定理求出点N到X轴距离,再利用数形结合思想得到点N的正确坐标。
P
x
O
M
y
N
长兴县泗安中学
ftp://192.168.150.50/
与《圆》有关中的计算
长兴县泗安中学九年级备课组(cjc)
(建议两课时)
(一)圆中有关角的计算。
(一)基本要求
(三)圆中有关位置的计算。
(二)圆中有关线段的计算。
(四)圆中有关公式的计算。
1.(2009温州)如图,∠AOB是⊙0的圆心角,∠AOB=80°,则弧AB所对圆周角∠ACB的度数是( )
A、40° B、45° C、50° D、80°
(一)圆中有关角的计算。
A
2.(2009年孝感)如图,⊙O是△ABC的外接圆,已知∠B=60°,则∠CAO的度数是( )
A.15° B.30° C.45° D.60°
(一)圆中有关角的计算。
B
2.(2009年孝感)如图,⊙O是△ABC的外接圆,已知∠B=60°,则∠CAO的度数是( )
A.15° B.30° C.45° D.60°
(一)圆中有关角的计算。
P
3.如图,在⊙O中, ∠ACB=120°,
求∠AOB的度数.
(一)圆中有关角的计算。
O
A
B
C
4.(2009温州)如图,在△ABC中,∠C=90°
,AC=3,BC=4.0为BC边上一点,以0为圆
心,OB为半径作半圆与BC边和AB边分别交
于点D、点E,连结DE.
当BD=3时,求线段DE的长;
(一)圆中有关角的计算。
(二)圆中有关线段的计算。
主要是圆的轴对称性的计算应用为主(专题复习)
回顾---垂径定理及逆定理
如图,在下列五个条件中:
只要具备其中两个条件,就可推出其余三个结论.
●O
A
B
C
D
M└
① CD是直径,
③ AM=BM,
② CD⊥AB,
⌒
⌒
④AC = BC,
⌒
⌒
⑤ AD = BD.
例1如图,已知⊙O的半径OA长为5,弦AB的长8,OC⊥AB于C,则OC的长为 _______.
O
A
B
C
3
AC=BC
弦心距
半径
半弦长
涉及知识:垂径定理、勾股定理
解题策略:主抓关键直角三角形
变式2:
如图, ⊙O 的直径CE⊥AB于点D,CD=AB=8cm,则⊙O 的半径为_____。
O
A
B
C
D
E
变式1:
如图, ⊙O 的直径CE⊥AB于点D,AB=8cm, DE=2cm,则⊙O 的半径为_____。
5
5
填一填
主要方法:设元法
(方程思想)
如图,在⊙O中,弦AB=8,⊙O的半径为5,P是弦AB上的一个动点,则OP的值有什么变化呢?
o
A
B
P
观察与思考
3 ≤ OP ≤ 5
变式1 过⊙O内一点D的最长弦长为10cm,最短弦长为8cm,那么OD长为( )
A.3 B.6cm C. cm D.9cm
A
O
A
B
C
D
E
画一画
最长的弦:过D点的直径
最短的弦:与过D点的直径相垂直的弦
已知⊙O的半径为10cm,点P是⊙O内一点,且OP=8,则过点P的所有弦中,最短的弦是( )
(A)6cm (B)8cm (C)10cm (D)12cm
D
10
8
6
变式2
变式3:已知⊙O的半径为5cm,点P是⊙O内一点,且OP=3cm,则过点P的所有弦中,弦长为整数的弦有几条
O
P
合作与探索
基本图形
(半径、半弦、弦心距构成的直角三角形)
1.如图,P为⊙O的弦BA延长线上一点,
PA=AB=2,PO=5,求⊙O的半径。
M
A
P
B
O
A
第一跳:
解题策略:作辅助线,借助两个直角三角形解决问题
如图所示,已知RtΔABC中,∠C=90°,AC= ,BC=1,若以C为圆心,CB为半径的圆交AB于P,则AP= 。
D
第二跳:
第三跳:
已知等腰ΔABC内接于⊙O,半径为5cm,底边BC长6cm,则其底边上的高是 。
按图形分类
1cm或9cm
两种方法:设元法、 简化构图法
一项策略:辅助线构建直角三角形
三个思想:建模、分类思想、方程思想
小结“一二三”
1.(2009年湖州)已知 与 外切,它们半径分别为2和3,则圆心距 长是( )
A. =1 B. =5 C.1< <5D. >5
2.(2009年台州)大圆半径为6,小圆半径为3,两圆圆心距为10,则两圆位置关系为( )
A.外离 B.外切 C.相交 D.内含
(三)圆中有关位置的计算。
B
A
(三)圆中有关位置的计算。
3.(2009年绍兴)如图, 、 的半径分别为1cm,2cm,圆心距AB为5cm.如果 由图示位置沿直线AB向右平移3cm,则此时该圆与 的位置关系是_____________.
B
A
相交
(三)圆中有关位置的计算。
4.(2009年潍坊)已知圆O的半径为R,AB是圆O的直径,D是AB延长线上一点,DC是圆O的切线,C是切点,连结AC,若∠ACB=300,则BD的长为( )
A.2 B. C. D.
(四)圆中有关公式的计算。
1.(2009年咸宁市)为庆祝祖国六十华诞,某单位排练的节目需用到如图所示的扇形布扇,布扇完全打开后,外侧两竹条AB、AC夹角为1200,AB的长为30cm,贴布部分BD的长为20cm,则贴布部分的面积约为________.cm2( 取3)
(四)圆中有关公式的计算。
2.(2007年湖州)已知扇形OBC、OAD的半径之间的关系是OB= OA,则BC的长是AD长的( )
A、 倍 B、2倍 C、 倍 D、4倍
A
B
C
D
O
(四)圆中有关公式的计算。
3.(2009年丽水)已知圆锥的底面半径
为3,母线长为4,则它的侧面积是( )
A. B. C. D. 12
4.(2009年义乌)如图,圆锥的侧面积为
,底面半径为3,则圆锥
的高AO为__________.
(四)圆中有关公式的计算。
5.(2009年台州)如图,三角板中,∠ACB=900,∠B=300,BC =6.三角板绕直角顶点C逆时针旋转,当点A的对应点A/落在AB边的起始位置上时即停止转动,则点转过的路径长为 .
主要是一些渗透数学思想方法的综合题
(二)较高要求与适度拓展
1. (2009年湖州)如图,已知在 中, , ,分别以AC、BC为直径作半圆,面积分别记为S1、S2,,则S1 + S2 的值等于 .
(二)较高要求与适度拓展
C
A
B
S1
S2
本题看似不可能,但
可以利用转化思想巧妙
地结合勾股定理,求出
S1 + S2的值,但两个“一半”
很容易导致计算错误。又如:
(2009年嘉兴)如图,⊙P内含于⊙O,⊙O的弦切⊙P于点C,且 .若阴影部分的面积为 ,则弦AB的长为( )
A.3 B.4 C.6 D.9
(二)较高要求与适度拓展
H
本题看似不可能,但通过转化思想,由阴影部分面积求出两圆半径的平方差,再综合垂经定理、勾股定理、平行线和切线的性质等知识,求出弦的半长。
2.(2009年绍兴)如图,在平面直角坐标系中, 与X轴相切于原点O,平行于y轴的直线交 于M、N 两点.若点M坐标(2,-1),则点N的坐标是( )
A(2,-4) B(2,-4.5) C(2,-5) D(2,-5.5)
(二)较高要求与适度拓展
本题通过辅助性和切线性质,构造一个直角三角形,利用方程思想求出圆的半径,再结合垂经定理求出点N到X轴距离,再利用数形结合思想得到点N的正确坐标。
P
x
O
M
y
N
长兴县泗安中学
ftp://192.168.150.50/
同课章节目录
