浙教版 九年级数学上学期 第3章 圆的基本性质 3.3 垂径定理 同步练习(Word版 含解析)
文档属性
| 名称 | 浙教版 九年级数学上学期 第3章 圆的基本性质 3.3 垂径定理 同步练习(Word版 含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 208.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-06 05:57:41 | ||
图片预览




文档简介
3.3
垂径定理
一.选择题
1.如图,⊙O的弦AB⊥OC,且OD=2DC,AB=2,则⊙O的半径为( )
A.1
B.2
C.3
D.9
2.抛一个铁球,在泥地上砸了一个直径8cm,深2cm的坑,这个铁球的直径是( )
A.12cm
B.10cm
C.8cm
D.6cm
3.圆O的半径为6cm,P是圆O内一点,OP=2cm,那么过点P的最短弦的长等于( )
A.cm
B.8
C.6cm
D.12cm
4.如图,在半径为4的⊙O中,弦AB∥OC,∠BOC=30°,则AB的长为( )
A.2
B.
C.4
D.
5.如图,⊙O的半径OA=6,以A为圆心,OA为半径的弧交⊙O于B、C点,则BC=( )
A.
B.
C.
D.
6.如图,在⊙O中,AB是直径,CD是弦,AB⊥CD,垂足为E,连接CO,AD,∠BAD=20°,则下列说法中正确的是( )
A.AD=2OB
B.CE=EO
C.∠OCE=40°
D.∠BOC=2∠BAD
7.半径等于12的圆中,垂直平分半径的弦长为( )
A.
B.
C.
D.
8.下列判断中正确的是( )
A.平分弦的直线垂直于弦
B.平分弦的直线也必平分弦所对的两条弧
C.弦的垂直平分线必平分弦所对的两条弧
D.平分一条弧的直线必平分这条弧所对的弦
二.填空题
9.如图,有一座石拱桥,上部拱顶部分是圆弧形,跨度BC=10m,拱高为(10﹣5)m,那么弧BC所在圆的半径等于
.
10.如图,在平面直角坐标系xOy中,以原点O为圆心的圆过点A(2,0),直线y=x+与⊙O交于B、C两点,则弦BC的长为
.
11.如图是一个圆环形黄花梨木摆件的残片,为求其外圆半径,小林在外圆上任取一点A,然后过点A作AB与残片的内圆相切于点D,作CD⊥AB交外圆于点C,测得CD=15cm,AB=60cm,则这个摆件的外圆半径是
cm.
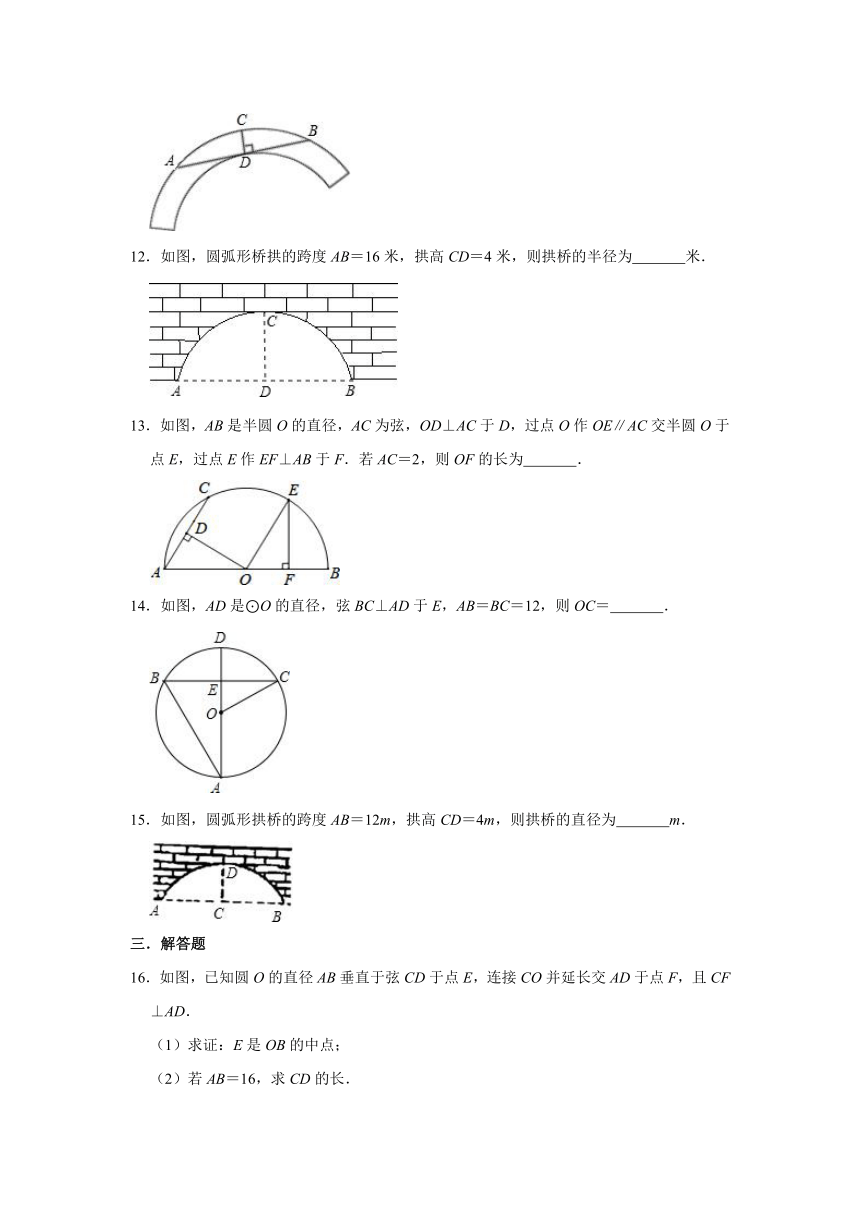
12.如图,圆弧形桥拱的跨度AB=16米,拱高CD=4米,则拱桥的半径为
米.
13.如图,AB是半圆O的直径,AC为弦,OD⊥AC于D,过点O作OE∥AC交半圆O于点E,过点E作EF⊥AB于F.若AC=2,则OF的长为
.
14.如图,AD是⊙O的直径,弦BC⊥AD于E,AB=BC=12,则OC=
.
15.如图,圆弧形拱桥的跨度AB=12m,拱高CD=4m,则拱桥的直径为
m.
三.解答题
16.如图,已知圆O的直径AB垂直于弦CD于点E,连接CO并延长交AD于点F,且CF⊥AD.
(1)求证:E是OB的中点;
(2)若AB=16,求CD的长.
17.如图,已知⊙O的直径d=10,弦AB与弦CD平行,它们之间的距离为7,且AB=6,求弦CD的长.
18.如图,已知⊙O的弦AB垂直平分半径OC,连接AO并延长交⊙O于点E,连接DE,若AB=4,请完成下列计算
(1)求⊙O的半径长;
(2)求DE的长.
19.如图,AB为⊙O的直径,弦CD⊥AB于E,已知CD=12,BE=2,求⊙O的直径.
20.在我国古代数学著作《九章算术》中记载了这样一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”用现代语言表述为:如图,AB为⊙O的直径,弦CD⊥AB于点E,AE=1寸,CD=10寸,求直径AB的长.
请你解答这个问题.
21.校运会期间,小捷同学积极参与各项活动.在铅球项目中,他掷出的铅球在场地上压出一个小坑(图示是其主视图),经测量,其中坑宽AB为8cm,小坑的最大深度为2cm,请帮助小捷同学计算铅球的半径OA的长为多少?
参考答案
一.选择题
1.解:设OD=2a,则CD=a,OA=3a,
∵AB⊥OC,OC为半径,
∴AD=BD=AB=,
在Rt△ODA中,由勾股定理得:(3a)2=(2a)2+()2,
a=1(负数舍去),
OA=3×1=3,
故选:C.
2.解:设该铅球的半径是rcm.
在由铅球的半径、小坑的半径即半弦和弦心距组成的直角三角形中,
根据勾股定理,得r2=(r﹣2)2+16,
解得r=5,
故2r=10.
故选:B.
3.解:过点P的最短弦是垂直于OP的弦CD,
连接OC.根据勾股定理,得PC==4,
再根据垂径定理,得CD=8.
故选:B.
4.解:延长BO交⊙O于点D,连接AD
∵BD是直径,
∴∠BAD=90°,BD=4×2=8
∵AB∥OC,∠BOC=30°,
∴∠ABD=30°
在Rt△ADB中,
∵∠ABD=30°,
∴AD=BD=4,
AB=
=
=4
故选:D.
5.解:设OA与BC相交于D点.
∵AB=OA=OB=6
∴△OAB是等边三角形.
又根据垂径定理可得,OA平分BC,
利用勾股定理可得BD==3
所以BC=6.
故选:A.
6.解:∵AB⊥CD,
∴=,CE=DE,
∴∠BOC=2∠BAD=40°,
∴∠OCE=90°﹣40°=50°.
故选:D.
7.解:如图,OA=12,则OC=6,
根据勾股定理可得,弦的一半==6,
∴弦=12.
故选:B.
8.解:A、平分弦(非直径)的直径垂直于弦,故本选项错误;
B、平分弦的直径也必平分弦所对的两条弧,故本选项错误;
C、弦的垂直平分线必平分弦所对的两条弧,符合垂径定理,故本选项正确;
D、平分一条弧的直径必平分这条弧所对的弦,故本选项错误.
故选:C.
二.填空题
9.解:设圆弧所在圆的圆心为O,半径为r,
连接OB,过O作OA⊥BC于D交于A,
则BD=BC=5,AD=10﹣5,
∴OD=r﹣10+5,
∵OB2=BD2+OD2,
∴r2=52+(r﹣10+5)2,
解得:r=10,
故答案为:10.
10.解:设直线y=x+与两坐标轴分别交于D、E点,过O点作OM⊥BC于点M,连接OB,如下图
由直线y=x+可知点D坐标为(0,),点E的坐标为(﹣3,0)
∴=
∴∠DEA=30°
∴OM=OE=
在Rt△OMB中,OM=,OB=OA=2
∴BM==
由垂径定理可知BC=2BM=×2=
故答案为.
11.解:如图,设点O为圆环的圆心,连接OA和OD,
∵AB是内圆O的切线,
∴AB⊥OD,
∴∠ADO=90°,
∵CD⊥AB,
∴∠ADC=90°,
∴∠ODC=180°,
∴O、D、C共线,
∴OC⊥AB,
∴AD=AB=30cm,
∴设OA为rcm,则OD=(r﹣15)cm,
根据题意得:r2=(r﹣15)2+302,
解得:r=37.5.
∴这个摆件的外圆半径长为37.5cm;
故答案为:37.5.
12.解:设所在的圆的圆心是O.
根据垂径定理,知C,O,D三点共线,
设圆的半径是r,则根据垂径定理和勾股定理,得r2=(r﹣4)2+64,∴r=10m.
13.解:∵OD⊥AC,AC=2,
∴AD=CD=1,
∵OD⊥AC,EF⊥AB,
∴∠ADO=∠OFE=90°,
∵OE∥AC,
∴∠DOE=∠ADO=90°,
∴∠DAO+∠DOA=90°,∠DOA+∠EOF=90°,
∴∠DAO=∠EOF,
在△ADO和△OFE中,
,
∴△ADO≌△OFE(AAS),
∴OF=AD=1,
故答案为:1.
14.解:如图,连接BD;
∵直径AD⊥BC,
∴BE=CE=BC=6;
由勾股定理得:
AE==6;
∵AD为⊙O的直径,
∴∠ABD=90°;
由射影定理得:
AB2=AE?AD
∴AD==8,
∴OC=AD=4,
故答案为4.
15.解:由题中已知条件可得,
AB=12,CD=4,AC=AB=6,
∴OC=R﹣CD=R﹣4,
∴R2=(R﹣4)2+62,
∴R=6.5(m),
∴2R=13(m).
答:拱桥的直径为13m.
三.解答题
16.(1)证明:连接AC,如图
∵直径AB垂直于弦CD于点E,
=,
∴AC=AD,
∵过圆心O的线CF⊥AD,
∴AF=DF,即CF是AD的中垂线,
∴AC=CD,
∴AC=AD=CD.
即:△ACD是等边三角形,
∴∠FCD=30°,
在Rt△COE中,OE=OC,
∴OE=OB,
∴点E为OB的中点;
(2)解:在Rt△OCE中,AB=16,
∴OC=AB=8,
又∵BE=OE,
∴OE=4,
∴CE===4,
∴CD=2CE=8.
17.解:作OM⊥AB于M,ON⊥CD于N,连接OA、OC,
则AM=AB=3,
∵AB∥CD,
∴点M、O、N在同一条直线上,
在Rt△AOM中,OM==4,
∴ON=MN﹣OM=3,
在Rt△CON中,CN==4,
∵ON⊥CD,
∴CD=2CN=8.
18.解:(1)连接BE,
∵⊙O的半径OC⊥弦AB于点D,AB=4,
∴AD=BD=2,
设OA=x,
∵OD=x,
在Rt△AOD中,AD2+OD2=OA2,
∴2+2=x2,
解得:x=4,
即⊙O的半径长是4;
(2)由(1)∴OA=OE=4,OD=2,
∴BE=2OD=4,
∵AE是直径,
∴∠B=90°,
∴DE=,
19.解:∵AB为⊙O的直径,弦CD⊥AB于E,CD=12,
∴DE=CD=6.
连接OD,设OD=r,则OE=r﹣2,在Rt△ODE中,
∵OE2+DE2=OD2,即(r﹣2)2+62=r2,解得r=10,
∴AB=2r=20.
20.解:如图所示,连接OC.
∵弦CD⊥AB,AB为圆O的直径,
∴E为CD的中点,
又∵CD=10寸,
∴CE=DE=CD=5寸,
设OC=OA=x寸,则AB=2x寸,OE=(x﹣1)寸,
由勾股定理得:OE2+CE2=OC2,
即(x﹣1)2+52=x2,
解得:x=13,
∴AB=26寸,
即直径AB的长为26寸.
21.解:作OD⊥AB于D,如图所示:
∵AB=8cm,OD⊥AB,小坑的最大深度为2cm,
∴AD=AB=4cm.
设OA=rcm,则OD=(r﹣2)cm
在Rt△OAD中,
∵OA2=OD2+AD2,即r2=(r﹣2)2+42,
解得r=5cm;
即铅球的半径OA的长为5cm.
垂径定理
一.选择题
1.如图,⊙O的弦AB⊥OC,且OD=2DC,AB=2,则⊙O的半径为( )
A.1
B.2
C.3
D.9
2.抛一个铁球,在泥地上砸了一个直径8cm,深2cm的坑,这个铁球的直径是( )
A.12cm
B.10cm
C.8cm
D.6cm
3.圆O的半径为6cm,P是圆O内一点,OP=2cm,那么过点P的最短弦的长等于( )
A.cm
B.8
C.6cm
D.12cm
4.如图,在半径为4的⊙O中,弦AB∥OC,∠BOC=30°,则AB的长为( )
A.2
B.
C.4
D.
5.如图,⊙O的半径OA=6,以A为圆心,OA为半径的弧交⊙O于B、C点,则BC=( )
A.
B.
C.
D.
6.如图,在⊙O中,AB是直径,CD是弦,AB⊥CD,垂足为E,连接CO,AD,∠BAD=20°,则下列说法中正确的是( )
A.AD=2OB
B.CE=EO
C.∠OCE=40°
D.∠BOC=2∠BAD
7.半径等于12的圆中,垂直平分半径的弦长为( )
A.
B.
C.
D.
8.下列判断中正确的是( )
A.平分弦的直线垂直于弦
B.平分弦的直线也必平分弦所对的两条弧
C.弦的垂直平分线必平分弦所对的两条弧
D.平分一条弧的直线必平分这条弧所对的弦
二.填空题
9.如图,有一座石拱桥,上部拱顶部分是圆弧形,跨度BC=10m,拱高为(10﹣5)m,那么弧BC所在圆的半径等于
.
10.如图,在平面直角坐标系xOy中,以原点O为圆心的圆过点A(2,0),直线y=x+与⊙O交于B、C两点,则弦BC的长为
.
11.如图是一个圆环形黄花梨木摆件的残片,为求其外圆半径,小林在外圆上任取一点A,然后过点A作AB与残片的内圆相切于点D,作CD⊥AB交外圆于点C,测得CD=15cm,AB=60cm,则这个摆件的外圆半径是
cm.
12.如图,圆弧形桥拱的跨度AB=16米,拱高CD=4米,则拱桥的半径为
米.
13.如图,AB是半圆O的直径,AC为弦,OD⊥AC于D,过点O作OE∥AC交半圆O于点E,过点E作EF⊥AB于F.若AC=2,则OF的长为
.
14.如图,AD是⊙O的直径,弦BC⊥AD于E,AB=BC=12,则OC=
.
15.如图,圆弧形拱桥的跨度AB=12m,拱高CD=4m,则拱桥的直径为
m.
三.解答题
16.如图,已知圆O的直径AB垂直于弦CD于点E,连接CO并延长交AD于点F,且CF⊥AD.
(1)求证:E是OB的中点;
(2)若AB=16,求CD的长.
17.如图,已知⊙O的直径d=10,弦AB与弦CD平行,它们之间的距离为7,且AB=6,求弦CD的长.
18.如图,已知⊙O的弦AB垂直平分半径OC,连接AO并延长交⊙O于点E,连接DE,若AB=4,请完成下列计算
(1)求⊙O的半径长;
(2)求DE的长.
19.如图,AB为⊙O的直径,弦CD⊥AB于E,已知CD=12,BE=2,求⊙O的直径.
20.在我国古代数学著作《九章算术》中记载了这样一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”用现代语言表述为:如图,AB为⊙O的直径,弦CD⊥AB于点E,AE=1寸,CD=10寸,求直径AB的长.
请你解答这个问题.
21.校运会期间,小捷同学积极参与各项活动.在铅球项目中,他掷出的铅球在场地上压出一个小坑(图示是其主视图),经测量,其中坑宽AB为8cm,小坑的最大深度为2cm,请帮助小捷同学计算铅球的半径OA的长为多少?
参考答案
一.选择题
1.解:设OD=2a,则CD=a,OA=3a,
∵AB⊥OC,OC为半径,
∴AD=BD=AB=,
在Rt△ODA中,由勾股定理得:(3a)2=(2a)2+()2,
a=1(负数舍去),
OA=3×1=3,
故选:C.
2.解:设该铅球的半径是rcm.
在由铅球的半径、小坑的半径即半弦和弦心距组成的直角三角形中,
根据勾股定理,得r2=(r﹣2)2+16,
解得r=5,
故2r=10.
故选:B.
3.解:过点P的最短弦是垂直于OP的弦CD,
连接OC.根据勾股定理,得PC==4,
再根据垂径定理,得CD=8.
故选:B.
4.解:延长BO交⊙O于点D,连接AD
∵BD是直径,
∴∠BAD=90°,BD=4×2=8
∵AB∥OC,∠BOC=30°,
∴∠ABD=30°
在Rt△ADB中,
∵∠ABD=30°,
∴AD=BD=4,
AB=
=
=4
故选:D.
5.解:设OA与BC相交于D点.
∵AB=OA=OB=6
∴△OAB是等边三角形.
又根据垂径定理可得,OA平分BC,
利用勾股定理可得BD==3
所以BC=6.
故选:A.
6.解:∵AB⊥CD,
∴=,CE=DE,
∴∠BOC=2∠BAD=40°,
∴∠OCE=90°﹣40°=50°.
故选:D.
7.解:如图,OA=12,则OC=6,
根据勾股定理可得,弦的一半==6,
∴弦=12.
故选:B.
8.解:A、平分弦(非直径)的直径垂直于弦,故本选项错误;
B、平分弦的直径也必平分弦所对的两条弧,故本选项错误;
C、弦的垂直平分线必平分弦所对的两条弧,符合垂径定理,故本选项正确;
D、平分一条弧的直径必平分这条弧所对的弦,故本选项错误.
故选:C.
二.填空题
9.解:设圆弧所在圆的圆心为O,半径为r,
连接OB,过O作OA⊥BC于D交于A,
则BD=BC=5,AD=10﹣5,
∴OD=r﹣10+5,
∵OB2=BD2+OD2,
∴r2=52+(r﹣10+5)2,
解得:r=10,
故答案为:10.
10.解:设直线y=x+与两坐标轴分别交于D、E点,过O点作OM⊥BC于点M,连接OB,如下图
由直线y=x+可知点D坐标为(0,),点E的坐标为(﹣3,0)
∴=
∴∠DEA=30°
∴OM=OE=
在Rt△OMB中,OM=,OB=OA=2
∴BM==
由垂径定理可知BC=2BM=×2=
故答案为.
11.解:如图,设点O为圆环的圆心,连接OA和OD,
∵AB是内圆O的切线,
∴AB⊥OD,
∴∠ADO=90°,
∵CD⊥AB,
∴∠ADC=90°,
∴∠ODC=180°,
∴O、D、C共线,
∴OC⊥AB,
∴AD=AB=30cm,
∴设OA为rcm,则OD=(r﹣15)cm,
根据题意得:r2=(r﹣15)2+302,
解得:r=37.5.
∴这个摆件的外圆半径长为37.5cm;
故答案为:37.5.
12.解:设所在的圆的圆心是O.
根据垂径定理,知C,O,D三点共线,
设圆的半径是r,则根据垂径定理和勾股定理,得r2=(r﹣4)2+64,∴r=10m.
13.解:∵OD⊥AC,AC=2,
∴AD=CD=1,
∵OD⊥AC,EF⊥AB,
∴∠ADO=∠OFE=90°,
∵OE∥AC,
∴∠DOE=∠ADO=90°,
∴∠DAO+∠DOA=90°,∠DOA+∠EOF=90°,
∴∠DAO=∠EOF,
在△ADO和△OFE中,
,
∴△ADO≌△OFE(AAS),
∴OF=AD=1,
故答案为:1.
14.解:如图,连接BD;
∵直径AD⊥BC,
∴BE=CE=BC=6;
由勾股定理得:
AE==6;
∵AD为⊙O的直径,
∴∠ABD=90°;
由射影定理得:
AB2=AE?AD
∴AD==8,
∴OC=AD=4,
故答案为4.
15.解:由题中已知条件可得,
AB=12,CD=4,AC=AB=6,
∴OC=R﹣CD=R﹣4,
∴R2=(R﹣4)2+62,
∴R=6.5(m),
∴2R=13(m).
答:拱桥的直径为13m.
三.解答题
16.(1)证明:连接AC,如图
∵直径AB垂直于弦CD于点E,
=,
∴AC=AD,
∵过圆心O的线CF⊥AD,
∴AF=DF,即CF是AD的中垂线,
∴AC=CD,
∴AC=AD=CD.
即:△ACD是等边三角形,
∴∠FCD=30°,
在Rt△COE中,OE=OC,
∴OE=OB,
∴点E为OB的中点;
(2)解:在Rt△OCE中,AB=16,
∴OC=AB=8,
又∵BE=OE,
∴OE=4,
∴CE===4,
∴CD=2CE=8.
17.解:作OM⊥AB于M,ON⊥CD于N,连接OA、OC,
则AM=AB=3,
∵AB∥CD,
∴点M、O、N在同一条直线上,
在Rt△AOM中,OM==4,
∴ON=MN﹣OM=3,
在Rt△CON中,CN==4,
∵ON⊥CD,
∴CD=2CN=8.
18.解:(1)连接BE,
∵⊙O的半径OC⊥弦AB于点D,AB=4,
∴AD=BD=2,
设OA=x,
∵OD=x,
在Rt△AOD中,AD2+OD2=OA2,
∴2+2=x2,
解得:x=4,
即⊙O的半径长是4;
(2)由(1)∴OA=OE=4,OD=2,
∴BE=2OD=4,
∵AE是直径,
∴∠B=90°,
∴DE=,
19.解:∵AB为⊙O的直径,弦CD⊥AB于E,CD=12,
∴DE=CD=6.
连接OD,设OD=r,则OE=r﹣2,在Rt△ODE中,
∵OE2+DE2=OD2,即(r﹣2)2+62=r2,解得r=10,
∴AB=2r=20.
20.解:如图所示,连接OC.
∵弦CD⊥AB,AB为圆O的直径,
∴E为CD的中点,
又∵CD=10寸,
∴CE=DE=CD=5寸,
设OC=OA=x寸,则AB=2x寸,OE=(x﹣1)寸,
由勾股定理得:OE2+CE2=OC2,
即(x﹣1)2+52=x2,
解得:x=13,
∴AB=26寸,
即直径AB的长为26寸.
21.解:作OD⊥AB于D,如图所示:
∵AB=8cm,OD⊥AB,小坑的最大深度为2cm,
∴AD=AB=4cm.
设OA=rcm,则OD=(r﹣2)cm
在Rt△OAD中,
∵OA2=OD2+AD2,即r2=(r﹣2)2+42,
解得r=5cm;
即铅球的半径OA的长为5cm.
同课章节目录
