4.5相似多边形

(共11张PPT)
4.5 相似多边形
对应角相等,对应边成比例的两个三角形叫做相似三角形.
对应角相等,对应边成比例的两个多边形叫做相似多边形.
定义:
类比思想
自主学习一
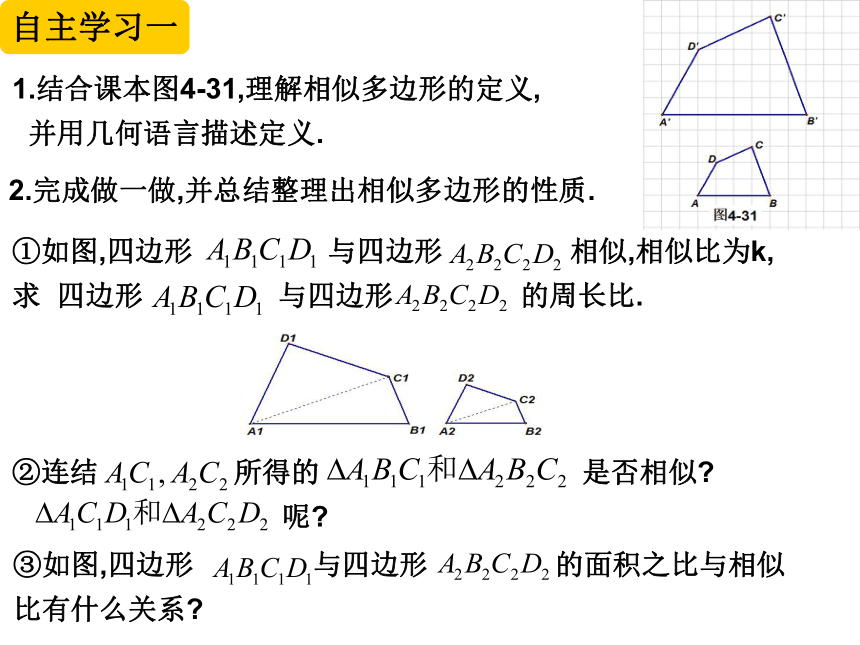
1.结合课本图4-31,理解相似多边形的定义,
并用几何语言描述定义.
2.完成做一做,并总结整理出相似多边形的性质.
①如图,四边形 与四边形 相似,相似比为k,求 四边形 与四边形 的周长比.
②连结 所得的 是否相似
呢
③如图,四边形 与四边形 的面积之比与相似比有什么关系
对应角相等,对应边成比例的两个多边形叫做相似多边形.
定义:
类比思想
性质:
相似多边形的周长之比等于相似比;
相似多边形的面积之比等于相似比的平方.
新 知 学 习
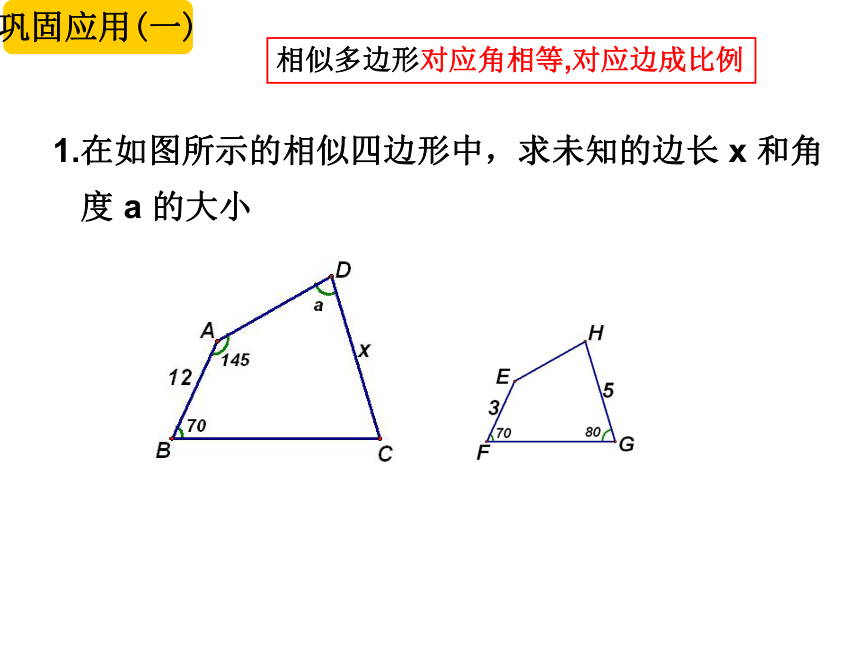
1.在如图所示的相似四边形中，求未知的边长 x 和角
度 a 的大小
巩固应用(一)
相似多边形对应角相等,对应边成比例
2.梯形ABCD中，AD∥BC，E是AB上的一点，EF∥BC，并且将梯形ABCD分成两个相似梯形AEFD、EBCF，若AD=4，BC=9.
①求线段EF的长度
②求AE：EB的值．
上题中若AD=2，BC=8，E点在何处时，EF所分梯形AEFD与梯形EBCF相似？
变式:
若EF是梯形ABCD的中位线,则EF所分成的两个梯形AEFD与梯形EBCF是否相似？
4
9
6
2
8
3.如图，把菱形ABCD沿对角线AC方向移动到菱形EFGH的位置，则重叠部分PEQC也是菱形。判断菱形PEQC与菱形ABCD是否相似.
若重叠部分面积是菱形ABCD面积的 ，建立如图所示的直角坐标系，求点E的坐标。
判断两个多边形是否相似,应从边和角两方面同时加以验证,即定义法.
自主学习二
阅读教材例题,思考以下问题:
1.题中对开后的两个矩形是什么关系
2.用定义来说明两个矩形相似关键在于说明哪一点
由此你能总结快速判断两个矩形相似的方法吗
3.用你总结的方法解决以下问题:
下列3个矩形中，相似的是________
①长8cm，宽6cm
②长8cm，宽4cm
③长为6cm，宽为4.5cm
分别计算两个矩形的长宽比值，观察是否相等
如图，把一个长方形划分成三个全等的长方形，若要使每一个小长方形与原小长方形相似，则原长方形应满足什么条件？
例题变式1:
拓 展 提 升
变式2:
如图,矩形ABCD∽矩形BCFE,且AD=AE,求AB:AD的值
回顾总结
本节课我们学习了：
1.相似多边形的定义: 对应角相等,对应边成比例的两个多边形.
2.相似多边形的性质:
相似多边形的周长之比等于相似比;
面积之比等于相似比的平方.
3.判断两个多边形相似的方法: 定义法
4.用相似多边形的性质解决一些特殊四边形中的几何问题.
类比思想