7.1常量与变量

(共14张PPT)
7.1常量与变量
浙教版八上第七章：一次函数
请同学们思考下面的问题：小红在网上查有关姚明哥哥的资料时发现，姚明哥哥的身体长高与自己在某一段时间内长速相同，于是她想到了下面问题：设姚明身高为y厘米，小红的身高为x厘米，姚明的身高是小红身高的2倍还多8厘米，你能找到用小红的身高来表示姚明的身高的关系式吗？
y=2x+8
在这个问题中你能说出哪些量是在变化的？哪些量是不变的？
X,y是在发生变化的，2，8是不变的。
请同学们思考下面问题：轿车速度为120千米/时，卡车的速度是80千米/时，两车同时同地同向出发，经t小时后两车相距s千米，你能找到t与s的等量关系吗？
S=40t
在上面的变化过程中哪些量是保持不变的？哪些量是在发生变化的？
40是不变的，t,s是在发生变化的。
随着人们生活水平的提高，现在许多人生病住院为了享受一对一的服务，特别请用护工，小明为住院的爷爷请了护工，小明家付给护工的工资如下表：
工作时间 1 2 3 4 … t
工资 15 27 39 51 …
（1）请回答护工的工资是怎样计算的？同时完成上表的空格。（2）护工的工资用w表示，请用t表示w,
(3)请说出这个问题的不变量和变化的量。
护工的工资是第一个小时15元，以后每小时12元。
12t+3
(2)W=12t+3
（3）这个问题中12和3是不变量，w,t是变量。
上面我们讨论的三个问题中我们分别得到了：
(1)y=2x+8 (2)s=40t (3)w=12t+3
我们把在某个研究过程中保持不变的量叫常量，在发生变化的量叫变量。
1.水果店橘子的单价为２.５元／千克，买m千克橘子的总价为w元，其中w与m的关系式为________________,这个问题中常量是____________;变量是____________.
⒉圆周长Ｃ与圆的半径r之间的关系式是____________,
常量是__________,变量是____________.
3.小明与小林在相距10千米的A，B两地背向而行，小明的速度是12千米/时，小林的速度是15千米/时，他们的运动时间为t小时，两人之间的距离为s,那么在这个问题中S与t的关系式为_________,常量是_______,变量是________
我们一起来试一试，相信你一定能正确地解决下面问题。
W=2.5m
2.5
W, m
C和r
S=27t+10
27和10
s和t
4.某山脚下的温度是15Ｃ0，向山上海拔升高100米，温度降低0.96C0,一批登山队员从山脚往上登山活动，他们上升的高度h米,在这一高度的温度TC0。这一问题中T与h的关系式为_____________.常量是________,变量是_________.
5.某种报纸每份a元，购买x份此种报纸共需y元，则 y与x的关系式为_________,常量是_________，变量是________。
6.在平面直角坐标系中点A（3，5）点B（2，0）点C是x轴上的一个动点，且从点B开始向右运动，速度是m单位/秒，
运动时间是t秒, △ABC面积为S，则s与t的关系式为 ____________,常量是_________,变量是_________。
T=15-0.0096h
15,0.0096
T,h
y=ax
a
y,x
S=2.5mt
2.5,m
S,t
我们发现：通常情况下，常数是常量，字母充当变量，但在特定意义的问题中字母也可以充当常量。
E
D
C
B
A
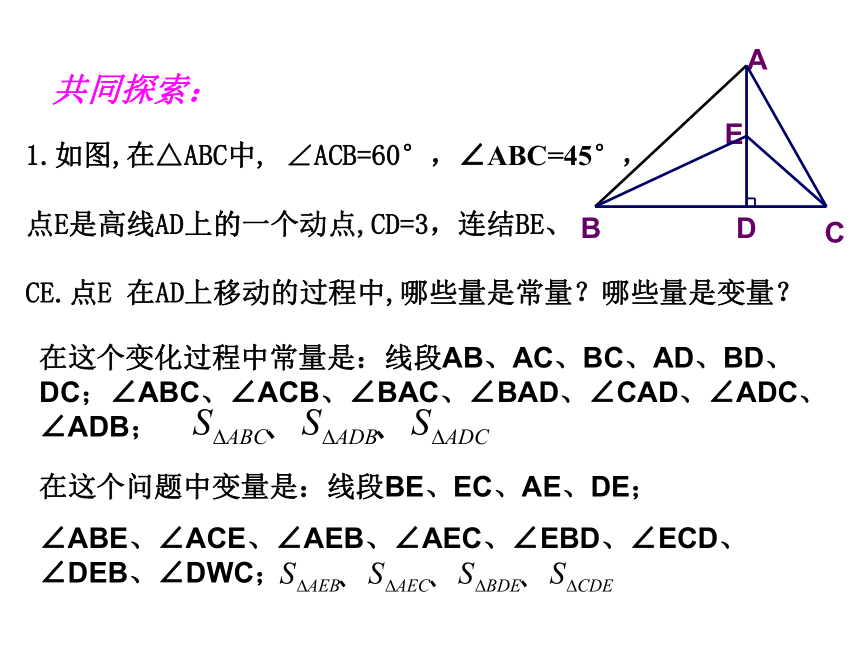
共同探索：
1.如图,在△ABC中, ∠ACB=60°，∠ABC=45°，
点E是高线AD上的一个动点,CD=3，连结BE、
CE.点E 在AD上移动的过程中,哪些量是常量？哪些量是变量？
在这个变化过程中常量是：线段AB、AC、BC、AD、BD、DC；∠ABC、∠ACB、∠BAC、∠BAD、∠CAD、∠ADC、∠ADB；
在这个问题中变量是：线段BE、EC、AE、DE；
∠ABE、∠ACE、∠AEB、∠AEC、∠EBD、∠ECD、∠DEB、∠DWC；
A
B
C
M
N
2. AB∥MN,在直线AB上有一动点C，在直线MN上有两定点M、N，在整个C点的运动过程中，哪些是常量？哪些是变量？
在这个过程中，常量是：△CMN的面积和高，线段MN的长；
变量是：线段CM、CN的长度。
在上面两个问题的探索过程中，我们得特别注意全面地找到研究过程所存在的不变量和发生变化的量。
3.前面我们在研究护工的工作时间和得到的工资问题时，我们已得到关系式：w=12t+3，完成下表：
工作时间 1 2 3 4 … 10 11 12 t
工资 …
从上面的填表探索w与t的对应值时你发现了什么？
15 27 39 51
123 135 147 12t+3
我们发现当t取定一个唯一值时，w也有并且只有一个值与之对应。
如果护工得到了99元工资，你能知道他工作了多少时间吗？
99=12t+3,解关于t的一元一次方程得:t=8,反过来我们同样发现，当w确定一个值时，t也只有一个值与之对应。
巩固提高：
1.三角形的一边长7cm,它的面积为S(cm2),这边上高为h(cm)的关系式是_______________,其中常量是_____,变量是_____________.
2.出租车起步价为8元，3公里以后每公里收费为1.8元，如果出租车行驶里程为x千米（x≥3），乘客所付车费为y元，则怎样用含有行驶里程数x的代数式表示乘客所付
车费y的关系式为：_____________,其中常量是_______
变量是_____________.
y=1.8x+2.6 (x ≥3)
3.若a，b分别表示父母亲身高,h男，h女分别表示儿女成人时身
高，有下列关系：h男＝０.５４（a+b ）
h女＝０.９７５（a+b）÷２ 成人你的身高是多少？
整个过程中指出常量和变量。
S，h
1.8,2.6
X,y
常量:0.54,0.975,2.变量:h,a,b
4.我们知道四边形的对角线有2条,五边形的对角线有5条,六边形的对角线有9条……
(1)多边形的对角线条数用S表示,则n边形对角线的条数.
请找出s,n之间的关第式.
(2)请指出这个过程中的常量与变量.
分析:
4-3
4-3
0
0
5-3
5-3
1
0
0
6-3
6-3
2
1
0
0
常量是:2,3 变量是:s,n
5.先看下面报道：美国“勇气号”火星车于北京时间２004年1月4日12时35分左右，在火星表面成功着陆，在着陆前的最后6分时间内，它是在耐高温表层的保护下，以1.9万千米/时的速度冲入130千米厚的火星大气层，在空气阻力的作用下，它在距火星表面8千米左右时，时速降至
1600千米/时，此时直径10多米的降落伞自动打开。火星车着陆前的最后6分时间内，火星车运动的时间、速度，火星车着陆前6分时的位置到着陆点的距离，火星车所受火星的引力这些量中，哪些是变量？哪些是常量？
变量是:时间,速度,引力;常量是:距离
在本问题中你还能找到哪些常量和变量
6.观察右图直棱柱，完成下表:
顶点(M) 棱(F) 面(N)
三棱柱
四棱柱
五棱柱
n棱柱
(1)请回答M,F,N三者之间的数量关系;
(2)请指出这个问题的常量和变量.
6 9 5
8 12 6
10 15 7
2n 3n n+2
M,F,N三者之间的关系是:M+N=F+2
这个问题中常量是:2;变量是:M.N,F
本堂课我们学习了:
1.在某个研究过程中保持不变的量称作常量(可以是常数也可以是字母),在发生变化的量称作变量(一般都为字母)
2.在一般的问题研究过程中我们总能把常量和变量通过等式把它们连接起来(我们指的关系式).
3.我们能够非常正确地区分出一个研究过程的常量与变量.