一元一次方程的复习

(共37张PPT)
一元一次方程的复习
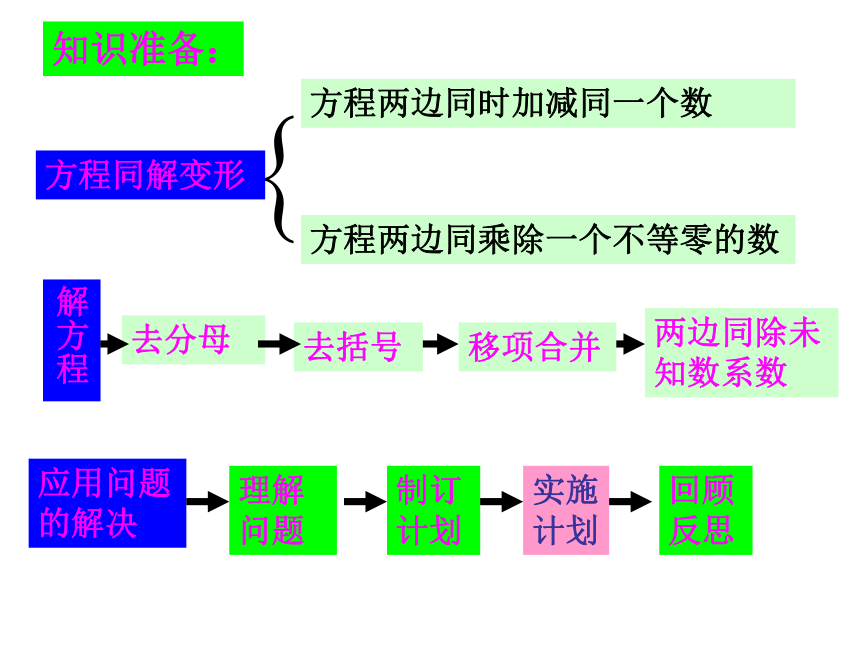
知识准备：
方程同解变形
方程两边同时加减同一个数
方程两边同乘除一个不等零的数
去分母
去括号
移项合并
解方程
两边同除未知数系数
应用问题的解决
理解问题
制订计划
实施计划
回顾反思
知识链接：
思索！
1．下列等式中是一元一次方程的是（　）
（ ）
3.已知x=－3是方程k(x+4)－x = 5的解，则k的值是（　　 ）Ａ.－２ Ｂ.２　 Ｃ.３　 Ｄ.５
4.方程∣2x-6∣=2的解是(　　)
Ａ.2　　 Ｂ.4　　 Ｃ. 2 Ｄ.2或4
5.设P=2y-2，Q=2y+3，且3P-Q=1，则y=( )
(A)0.4 (B)2.5 (C)－0.4 (D)－2.5
C
A
B
D
B
6.一个数的3倍比它的2倍多10，若设这个数为x，可得到方程____________。
7.关于x的两个方程5x－3=4x与ax－12=0的解相同，则a=_______。
8.已知轮船顺水前进的速度为m千米/时，水流速度为2千米/时，则轮船在静水中的速度是____千米/时。
9.三个连续奇数的和是75，这三个数分别是_______。
3X-2X=10
4
(m-2)
23, 25, 27
第一
12解下列方程（1）4x－3(20－x)= 3
解：去括号得：4x-60+3x=3 移项合并得：7x=63
方程两边同除以7得：x=9
例题赏识：
例3.某“希望学校”修建了一栋4层的教学大楼，每层楼有6间教室，进出这栋大楼共有3道门（两道大小相同的正门和一道侧门）. 安全检查中，对这3道门进行了测试：当同时开启一道正门和一道侧门时，2分钟内可以通过400名学生，若一道正门平均每分钟比一道侧门可多通过40名学生.
（1）求平均每分钟一道正门和一道侧门各可以通过多少名学生？
（2）检查中发现，紧急情况时因学生拥挤，出门的效率降低20%. 安全检查规定：在紧急情况下全大楼的学生应在5分钟内通过这3道门安全撤离. 假设这栋教学大楼每间教室最多有45名学生，问这三道门是否符合要求？为什么？
相关信息（1）大楼中共有学生=4×6×45=1080（人）
（2）三道门：一正门一侧门2分钟通过400人，一正门每分钟比一侧门多通过40人。
（3）紧急情况时因学生拥挤，出门的效率降低20%.
（4）紧急情况下全大楼的学生应在5分钟内安全撤离.
（1）解：设正常情况下一道侧门每分钟可通过x人，则一道正门每分钟可通过（x+40)人
由题意可得：2x+2(x+40)=400
解得：x=80
答：正常情况下一道侧门每分钟可通过80人，一道正门每分钟可通过120人。
（2）解：紧急情况下5分钟内可安全撤离学生：0.8×5×320=1280＞ 4×6×45=1080
因此此大楼的设计符合要求，能完成按规定安全撤离学生。
例4.现将自然数1至2004按图中的方式排成一个长方形阵列，用一个正方形框出9个数，
（1）图中的9个数的和是多少？
（2）能否使一个长方形框出的9个数
的和为2007？若不可能，请说明理由，
若可能，求出9个数中最大的数。
提升练习：
1．一根长18米的铁丝围成一个长是宽的2倍的长方形的面积为_____。
2．一件衬衫进货价60元,提高50%标价为______, 八折优惠价为______, 利润为______；
3．若关于x的方程3x+5=0与3x+2k= -1的解相同，则k=___
4．已知关于x的方程ax+b=c的解是x=1,则 =____
5.成都至重庆铁路全长504千米. 一辆快车以90千米/时的速度从重庆出发，1小时后，另有一辆慢车以48千米/时的速度从成都出发，则慢车出发＿＿小时后两车相遇。
6.方程 的解是x=-2，则a等于（ ）
A -8 B 0 C 2 D 8
7．某种品的标价为120元，若以九折降价出售，相对于进货价仍获利20%，该商品的进货价为（　　）。
　A．80元　　 B．85元　　C．90元　 D．95元
8．小山向某商人贷款1万元月利率为6‰ ，1年后需还给商人多少钱（　　）A 17200, B 16000,C 10720, D 10600
18
90
72
12
2
1
3
D
C
C
9.解下列方程（1）
(3)设
当x为何值时 与 互为相反数
爸爸等一下,让我算一算,换一种方式买票是否可以省钱.
大人门票是每张35元,学生门票是5折优惠,我们一共12人,共需350元.
票价
成人:每张35元, 学生:按成人票的5折优惠,
团体票:(16人以上含16人)按成人票的6折优惠.
10.在”五一”期间,小明和小亮等同学随家长一起到某公园游玩,上面是小明与他的爸爸在公园门口为买票的对话,试根据中图中的信息解答下面的问题.
(1)小明他们一共去了几个成人 几个学生
(2)请你帮助小明算一算,怎样买票更省钱 说明理由.
本题重要信息:(1)成人票35元一张, 学生票是成人票的一半,按此条件买票需350元钱. (2)团体票16人以上6折. (3)共12人.
(1)解:设成人x人,则学生(12-x)人
由题意可得:35x+17.5(12-x)=350
解得:x=8 答小明他们去的成人8人,学生4人,
(2)小明他们直接购买团体票,
所产生的费用=16×35×0.6=336＜350
因此小明他们还是直接购买团体票更省钱.
11.某购物广场文具部的某种毛笔每枝售价25元,书法练习本每本售价5元,该文具部制订了两种优惠方法:
A:买一枝毛笔送一本书法练习本;
B;按购买金额的九折付款.
某校打算为书法兴趣小组购买毛笔10枝,书法练习本x本(x≥10) (1)当x=40时,选用哪种优惠方法更合算 x=100呢
(2)当x为多少时其实这两种优惠方法所付的金额是一样的.
解(1)方法A:10×25+30×5=400
方法B:0.9×(10×25+40×5)=405 ∴X=40时,方法A合算.
当x=100时,A方法=700,B方法=675 ∴B方法合算.
(2)解:250+5(x-10)=0.9(250+5x) 解得:x=50
答当书法练习本是50本时,两种优惠方法所付金额是一样的.
一天，小马虎的爸爸大马虎请客，他看到几个人没来，就自言自语：“怎么该来的不来呢？”客人听了，觉得自己是不该来的，于是有一半客人走了，他一看十分着急，又说“哎，不该走的倒走了！”剩下的人一听 ，是我们该走啊！剩下的人中又有三分之二离开了，他着急地一拍大腿，连说：“我又不是说他们.”于是剩下的3个人也都走了，聪明的你知道开始来了多少客人吗？
解：设开始来了x位客人，可得：
小马虎的解法：
解得：
答：开始来了4人。
审
解
列
设
验（答）
星期天的早晨,马虎的妈妈带马虎和亲戚家的1位小朋友去温州乐园游玩。甲旅行社的促销办法是“带队的一位大人买全票，其余小朋友按团体票即半价优惠”；乙旅行社的促销办法是“包括带队的大人在内，一律按全票的六折优惠”。如果两家的服务质量相同，票价每张均是90元。那么，你知道吗：
（1）小孩人数为多少时，两家旅行社收费总数一样？
（2）马虎的妈妈会选择哪家旅行社呢？
（1）分析：数量有:
甲旅行社收费总数=乙旅行社收费总数
情境1：
人数、票价、收费总数
相等关系:
去玩了！
(2)解:
甲旅行社收费为
乙旅行社收费为
90×60﹪×3=162
答:马虎妈妈会选择乙旅行社
元
元
(1)解:
小孩有为x人时，两家旅行社收费总数一样
根据题意，
得
解这个方程，得
X=4
答:小孩有为4人时，两家旅行社收费总数一样
情境２：下午，从温州乐园回到家，马虎想起今天是爸爸的生日。在今年十二月份的日历上，他爸爸生日那天的上、下、左、右的4个日期的和为88，你知道他爸爸的生日是哪一天吗？(只列方程不解答)
分析：若设他爸爸生日
那天的日期为x,则生日
那天的上、下、左、右
的四个日期是：
x
x+1
x-1
x-7
X+7
解：
设他爸爸生日那天的日期是x，
根据题意，
（x-7）+（x+7）+（x-1）+（x+1）=88
得
本金+利息=本利和
解：
设马虎一共存了x年，
根据题意，得
200×1.98%x=207.92-200
解：
设马虎一共存了x年，根据题意，得
列式二:
列式一:
200+200×1.98%x=207.92
分析：利息=本金×利率×时间
情境3:为了给爸爸过生日，经由妈妈同意，马虎决定去银行取出自己的压岁钱，给爸爸买蛋糕。马虎把200元钱存入银行，年利率为1.98% ，一共取出207.92元，你知道他一共存了多少年吗？(只列方程不解答)
情境4:买完蛋糕，马虎为了赶在爸爸回家前先回到家，给他一个惊喜，马虎决定打的回家。温州出租车收费标准是：起步价（即不超过4千米）为10元；里程超过4千米以后每千米加价1.2元，马虎共花了17.5元，你知道小哲一共乘了多少千米吗？ (只列方程不解答)
分析：若设小哲一共乘了x千米，涉及到的数量关系如下表：
里程（千米）
收费（元）
总费用(元)
10+1.2（ x-4）
小于等于4
超过4即x-4
10
1.2（ x-4）
解：
设小哲一共乘了x千米，根据题意，得
10+1.2（ x-4）=17.5
情境5:爸爸刚回到家，就迫不急待地说：马虎，我有一件礼物要送给你，不过你要先回答好我的问题。他说：我们公司为了提高生产效益，准备派一些员工出差学习。有10人去杭州，有3人去上海，需从去杭州的人中调多少人到上海，使得去杭州的是去上海的人数的2倍多1人。 (只列方程不解答)
分析： 数量关系如下所示： 杭州 上海
调动前人数：
调动后人数：
10- x
等量关系：调动后去杭州的人数=调动后去上海人数的2倍多1人
x
加油噢
3
10
3+ x
解：
设需从去杭州的人中调x人到上海，
根据题意，得
10- x=2（ 3+ x ）+1
情境6：马虎轻松破解难题，他接下礼物，原来爸爸在开泰大厦为他买了他盼望已久的高级五彩橡皮泥。马虎灵机一动说：“爸爸，我也有一个小问题，如果你能答对，我也送你一件礼物。若用一块橡皮泥先做成一个圆柱体，其半径为1cm,高为9 cm，再把它改成立方体，你知道立方体的表面积吗？（圆柱体体积=底面积×高， ）
9cm
1cm
分析: 等量关系:圆柱体的体积=立方体的体积
解：
设立方体的棱长为x cm
根据题意，得
p
×12×9=x3
解这个方程，得
X=3
3×3×6=54cm2
答：立方体的表面积为54cm2
情境7：马虎的妈妈所在的服装厂加工车间有工人54人，
每人每天可加工上衣8件或裤子10条，应怎样合理分配
人数，才能使每天生产的上衣和裤子配套？
马虎的爸爸就要出差了，为了经常与家人联系，他将选择哪种手机卡更合算呢？全球通手机卡收费每分钟0.20元，月租每月20元；神州行手机卡没有月租费，每分钟0.4元（限本市通话）。
（1）当一个月通话时间多少分钟时，使用这两种手机的费用相同？
（2）针对这两种手机卡，从经济角度考虑，马虎的爸爸将如何选择？
我们一起来探究
1.下列方程是一元一次方程的是 ( )
A.x+2y=5 B. =2
C.x2=8x-3 D. y=1
2.下列方程中，解是x=2的是 ( )
A.2x-2=0 B. x=4
C.4x=2 D. -1=
3.将方程5x-1=4x变形为5x-4x=1，这个过程利用的性质是 ( )
A.等式性质1 B.等式性质2
C.移项 D.以上说法都不对
4.方程3- =1变形如下，正确的是 ( )
A.6-x+1=2 B.3-x+1=2
C.6-x+1=1 D.6-x-1=2
5.如果x=-8是方程3x+8= - a的解，则a的值为 ( )
A.-14 8.14 C.30 D.-30
6.某工作，甲单独完成需4天，乙单独完成需8天，现甲先工作1天后和乙共同完成余下的工作，甲一共做了 ( )
A.2天 B.3天 C.4天 D.5天
8.某种商品的标价为132元.若以标价的9折出售，仍可获利10％，则该商品的进价为 ( )
A.105元 B.100元 C.108元 D.118元
9.某工地调来72人挖土和运土，已知3人挖的±1人恰好能全部运走，怎样调配劳动力才能使挖出来的土能够及时运走且不窝工，解决此问题可设x人挖土，其他人运土，列方程
(1) =3；(2)72-x= ；(3) =3；(4)x+3x=72，上述所列方程正确的是 ( )
A.1个 B.2个 C.3个 D.4个
10.某轮船在两个码头之间航行，顺水航行需4h，逆水航行需6h，水流速度是2km／h，求两个码头之间的距离，我们可以设两个码头之间的距离为xkm，得到方程 ( )
13.已知5x+3=8x-3和 = 这两个方程的解是互为相反数，则a= .
.国家规定个人发表文章、出版图书获得稿费的纳税计算办法是：(1)稿费低于800元的不纳税；(2)稿费高于800元，又不高于4000元，应纳超过800元的那一部分稿费的14％的税；(3)稿费高于4000元，应缴纳全部稿费的11％的税.某作家缴纳了280元税，那么他获得的稿费是 元.
如图，小明将一个正方形纸片剪去一个宽为4厘米的长条后，再从剩下的长方形纸片上剪去一个宽为5厘米的长条，如果两次剪下的长条面积正好相等，那么每一个长条的面积为多少
一项工程，由甲队独做需12个月完工，由乙队独做需15个月完工.现决定由两队合作，且为了加快进度，甲、乙两队都将提高工作效率.若甲队的工作效率提高40％，乙队的工作效率提高25％，则两队合作，几个月可以完工
)某市按以下规定收取每月水费：若每月每户用水不超过20立方米，则每立方米水价按1.2元收费；若超过20立方米，则超过部分每立方米按2元收费.如果某居民在某月所交水费的平均水价为每立方米1.5元，那么这个月他共用了多少立方米水
小强、小芳、小亮在郊游，看到远处一列火车匀速通过一个隧道后，产生了以下对话.各位同学，请根据他们的对话求出这列火车的长.
温州和杭州某厂同时生产某种型号的机器若干台，温州厂可支援外地10台，杭州厂可支援外地4台.现在决定给武汉8台，南昌6台.每台机器的运费如下表.设杭州运往南昌的机器为x台.
(1)用x的代数式来表示总运费(单位：百元)；
(2)若总运费为8400元，则杭州运往南昌的机器应为多少台
终点
起点 南昌 武汉
温州厂 4 8
杭州厂 3 5
(3)试问有无可能使总运费是7400元 若有可能，请写出相应的调运方案；若无可能，请说明理由.