浙教版初中数学八年级上册 1.4 全等三角形 课件(共30张ppt)
文档属性
| 名称 | 浙教版初中数学八年级上册 1.4 全等三角形 课件(共30张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-11 21:44:00 | ||
图片预览









文档简介
合作学习,共同提高
努力造就实力,态度决定一切
如图古代有一将军,每天都要从驻地A处出发,到河边饮马,再到同岸的军营B处巡视,请问他应该怎么走才能使路程最短?
趣味问题(将军饮马)
2.1图形的轴对称
2.1图形的轴对称
北京故宫
整个宫殿建筑布局沿中轴线向东西两侧展开,呈现轴对称的结构。
由于轴对称给人以美感,它被广泛应用于建筑设计上。
凯旋门(法国巴黎)
自然中的对称美
剪纸艺术
聪明的你一定能够看出这些图形共同的特点.
如果一个图形沿着一条直线折起来,直线两侧的部分能够相互重合,那么这个图形叫做轴对称图形,这条直线就是它的对称轴。
概念
对称轴两侧能互相重合的两个点叫做对称点。
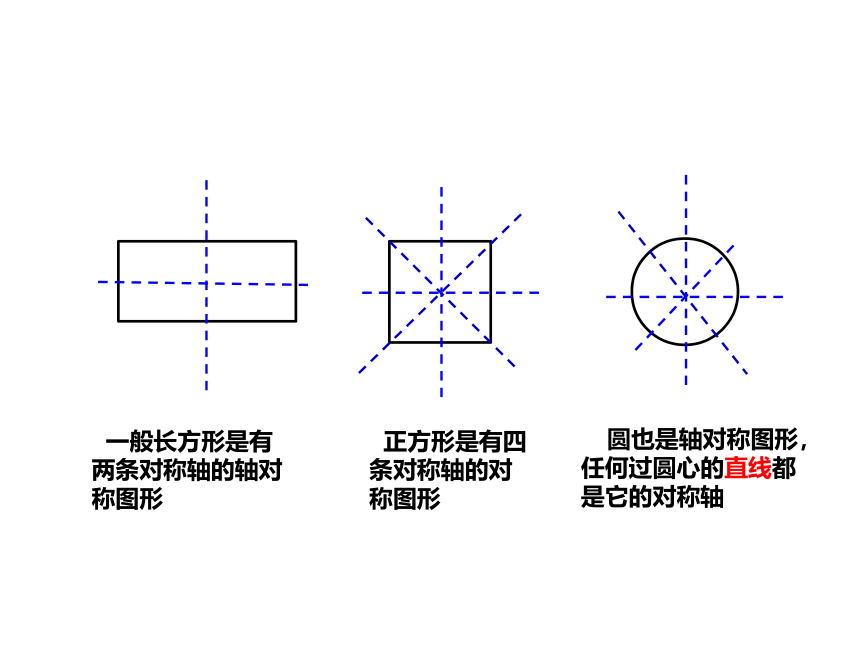
一般长方形是有两条对称轴的轴对称图形
圆也是轴对称图形,任何过圆心的直线都是它的对称轴
正方形是有四条对称轴的对称图形
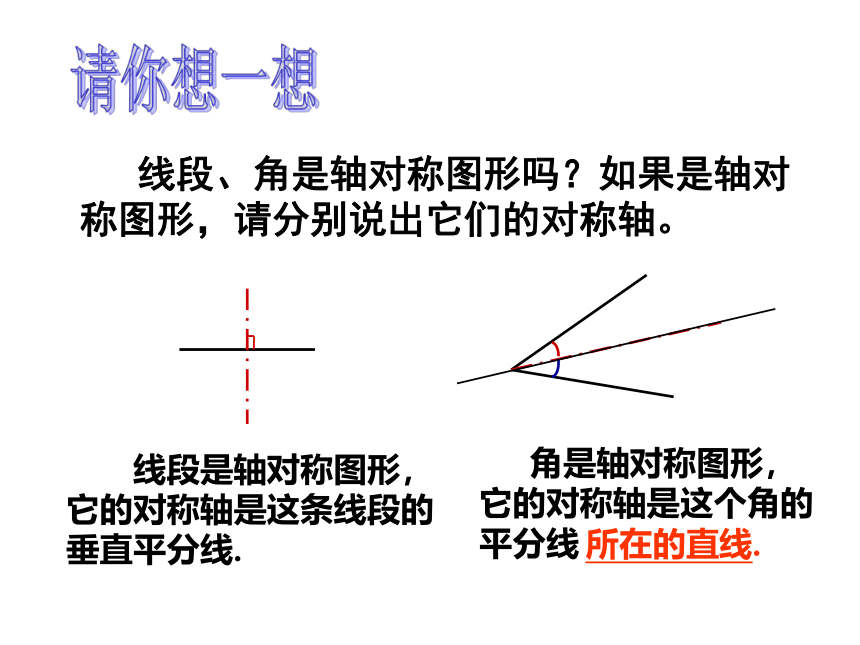
线段、角是轴对称图形吗?如果是轴对称图形,请分别说出它们的对称轴。
请你想一想
线段是轴对称图形,它的对称轴是这条线段的垂直平分线.
角是轴对称图形,它的对称轴是这个角的平分线
所在的直线.
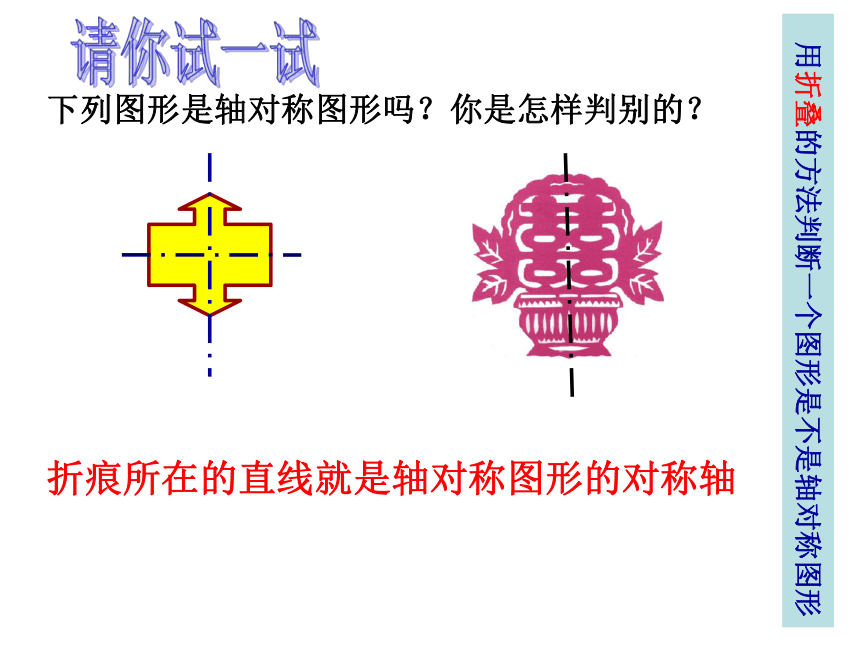
下列图形是轴对称图形吗?你是怎样判别的?
用折叠的方法判断一个图形是不是轴对称图形
请你试一试
折痕所在的直线就是轴对称图形的对称轴
A
不通过折叠
又如何画出轴对称图形的对称轴?
B
A
B
l
m
连结两个对称点之间的线段垂直平分线就是轴对称图形的对称轴
如果一个图形是轴对称图形,那么它的对称轴垂直平分连结两个对称点的线段.
合作学习
E
D
C
B
A
2
1
对称轴AD垂直平分两个对称点的连线BC。
轴对称图形的性质
对称轴垂直平分连结两个对称点的线段
换句话说
连结两个对称点之间的线段垂直平分线就是轴对称图形的对称轴
A
B
m
例
m
A
B
D
C
如图,四边形ABCD是轴对称图形。
(1)作出该图形的对称轴;
(2)若点E在四边形内,作出它的对称点E’。
E
E’
提示:
对称轴垂直平分连结两个对称点的线段
1、作轴对称图形的对称轴,一般步骤是:
请你理一理
找一组对称点
画对称点连线
作连线的垂直平分线
2、作轴对称图形上已知点的对称点,一般步骤是:
过已知点作对称轴的垂线
截取等长的线段
m
如果沿着直线m折叠,那么△A’B’C’就和△ABC重合,
这时我们说△A’B’C’和△ABC关于直线m成轴对称
B
C
A
B’
A’
C’
例1 已知△ABC和直线m.以直线m为对称轴,求作以点A,B,C的对称点A’,B’,C’为顶点的△A’B’C’.
由一个图形变为另一个图形,并使这两个图形沿某一条直线折叠后能够互相重合,我们称这两个图形关于某直线成轴对称,这条直线叫做对称轴。
成轴对称的两个图形是全等图形
成轴对称的两个图形形状和大小不变,什么改变了呢?
位置和方向改变。
m
如下图,已知线段AB和直线m,以直线m为对称轴,作与线段AB成轴对称的图形.
试一试
A
B
B’
我们称 线段AB和线段AB’关于直线m成轴对称。
成轴对称的两条线段长短不变,但改变了位置和方向。
如图古代有一将军,每天都要从驻地A处出发,到河边饮马,再到同岸的军营B处巡视,请问他应该怎么走才能使路程最短?
A’
P
C
m
也就是问P点在何处,AP+PB最短?
由轴对称性质得 AP=A’P
则 AP+BP=A’P+PB
1、哪一个是小明镜子里的像?
用一用
2、请说出两个孩子各是几号队员
用一用
3、平面镜中看到一挂钟如图所示,则此挂钟此时的实际时间是几点?
4、 一个汽车车牌在水中的倒影如图所示,你能确定该车的牌照号码吗?
用一用
练习
将一张三角形纸片的顶点A折叠到固定的A’位置,画出折痕,和折叠后的图形。
A
B
C
A’
如图,是由三个小正方形组成的图形,请你补画一个小正方形,使补画后的图形为轴对称图形,并画出对称轴。
请你试一试
1
2
3
请你试一试
2.1图形的轴对称
1.定义:轴对称图形(折叠重合)
对称轴(直线)
对称点
折痕所在的直线就是轴对称图形的对称轴;
连结两个对称点之间的线段垂直平分线就是轴对称图形的对称轴
2.性质:对称轴垂直平分连结两个对称点的线段
3.性质:成轴对称的两个图形是全等图形
教学思考与反思
本节的重点是图形的轴对称的概念和性质,而轴对称图形谁学生在小学就已经建立起了一个感性的认识,课本上的概念也是通过折叠的方法来定义的,所以在教学中也是运用定义来判断。
数学教学要揭示数学知识的本质,不能仅凭感观认识来判断,我设计了一个试一试折叠折痕和不折叠找对称轴的环节,目的使学生从两方面认识对称轴:①折痕所在的直线是对称轴②连接两个对称点之间的线段垂直平分线是对称轴。继续运用课本中合作学习,通过对一个具有轴对称性的四边形的探索,让学生逐步认清轴对称图形的性质,对称轴垂直平分连结两个对称点线段。
对于课本例1的教学我思考很久,到底如何进行例1的教学,它起到什么作用?其实例1既是轴对称性质的运用,又是给出“两个图形成轴对称”概念。既然是轴对称图形性质的运用,一下子给出三个顶点和一个三角形这样复杂图形,恐学生一下子难以接受,我适时做个铺垫,先引入一个具有轴对称的四边形,找对称轴,再作四边形内一点的对称点,让学生运用性质思考和演示相结合,然后,让学生动手操作例1,再给出“两个图形成轴对称”概念。
新教材中不提轴对称变换,而改成写“这样的图形改变叫做图形的轴对称”,前面例1中引出的说法是“两个三角形关于直线成轴对称”这样显得概念太多,我认为学生对突如其来的这么多似是而非的概念会更为迷糊,所以我不提“这样的图形改变叫做图形的轴对称”,而是仍然延用“两个图形关于直线成轴对称”这一说法。显得简洁明了。
例2是我感觉尤为困惑,特难处理的一个环节,如同鸡肋,食之无味弃之可惜。尤其是其证明环节,很难理解,但它又是几何图形求最值的经典之作,不可舍不可弃。学习轴对称很大程度上也是为了求几何最值,如何把握这一经典之作,让学生能理解又记忆深刻呢?我采用先入为主,课前就提出这问题,将军饮马,求一折线和的最小值。让后通过对轴对称的学习,明确轴对称不改变大小但能改变图形方向,引导学生改变线段方向,将折线变形为另一“有可能三点共线的折线”,学生能理解到两点之间线段最短,我想就已经达到目的,至于课本中运用任意点情况的证明,这一方法实在是难以让学生接受。
努力造就实力,态度决定一切
如图古代有一将军,每天都要从驻地A处出发,到河边饮马,再到同岸的军营B处巡视,请问他应该怎么走才能使路程最短?
趣味问题(将军饮马)
2.1图形的轴对称
2.1图形的轴对称
北京故宫
整个宫殿建筑布局沿中轴线向东西两侧展开,呈现轴对称的结构。
由于轴对称给人以美感,它被广泛应用于建筑设计上。
凯旋门(法国巴黎)
自然中的对称美
剪纸艺术
聪明的你一定能够看出这些图形共同的特点.
如果一个图形沿着一条直线折起来,直线两侧的部分能够相互重合,那么这个图形叫做轴对称图形,这条直线就是它的对称轴。
概念
对称轴两侧能互相重合的两个点叫做对称点。
一般长方形是有两条对称轴的轴对称图形
圆也是轴对称图形,任何过圆心的直线都是它的对称轴
正方形是有四条对称轴的对称图形
线段、角是轴对称图形吗?如果是轴对称图形,请分别说出它们的对称轴。
请你想一想
线段是轴对称图形,它的对称轴是这条线段的垂直平分线.
角是轴对称图形,它的对称轴是这个角的平分线
所在的直线.
下列图形是轴对称图形吗?你是怎样判别的?
用折叠的方法判断一个图形是不是轴对称图形
请你试一试
折痕所在的直线就是轴对称图形的对称轴
A
不通过折叠
又如何画出轴对称图形的对称轴?
B
A
B
l
m
连结两个对称点之间的线段垂直平分线就是轴对称图形的对称轴
如果一个图形是轴对称图形,那么它的对称轴垂直平分连结两个对称点的线段.
合作学习
E
D
C
B
A
2
1
对称轴AD垂直平分两个对称点的连线BC。
轴对称图形的性质
对称轴垂直平分连结两个对称点的线段
换句话说
连结两个对称点之间的线段垂直平分线就是轴对称图形的对称轴
A
B
m
例
m
A
B
D
C
如图,四边形ABCD是轴对称图形。
(1)作出该图形的对称轴;
(2)若点E在四边形内,作出它的对称点E’。
E
E’
提示:
对称轴垂直平分连结两个对称点的线段
1、作轴对称图形的对称轴,一般步骤是:
请你理一理
找一组对称点
画对称点连线
作连线的垂直平分线
2、作轴对称图形上已知点的对称点,一般步骤是:
过已知点作对称轴的垂线
截取等长的线段
m
如果沿着直线m折叠,那么△A’B’C’就和△ABC重合,
这时我们说△A’B’C’和△ABC关于直线m成轴对称
B
C
A
B’
A’
C’
例1 已知△ABC和直线m.以直线m为对称轴,求作以点A,B,C的对称点A’,B’,C’为顶点的△A’B’C’.
由一个图形变为另一个图形,并使这两个图形沿某一条直线折叠后能够互相重合,我们称这两个图形关于某直线成轴对称,这条直线叫做对称轴。
成轴对称的两个图形是全等图形
成轴对称的两个图形形状和大小不变,什么改变了呢?
位置和方向改变。
m
如下图,已知线段AB和直线m,以直线m为对称轴,作与线段AB成轴对称的图形.
试一试
A
B
B’
我们称 线段AB和线段AB’关于直线m成轴对称。
成轴对称的两条线段长短不变,但改变了位置和方向。
如图古代有一将军,每天都要从驻地A处出发,到河边饮马,再到同岸的军营B处巡视,请问他应该怎么走才能使路程最短?
A’
P
C
m
也就是问P点在何处,AP+PB最短?
由轴对称性质得 AP=A’P
则 AP+BP=A’P+PB
1、哪一个是小明镜子里的像?
用一用
2、请说出两个孩子各是几号队员
用一用
3、平面镜中看到一挂钟如图所示,则此挂钟此时的实际时间是几点?
4、 一个汽车车牌在水中的倒影如图所示,你能确定该车的牌照号码吗?
用一用
练习
将一张三角形纸片的顶点A折叠到固定的A’位置,画出折痕,和折叠后的图形。
A
B
C
A’
如图,是由三个小正方形组成的图形,请你补画一个小正方形,使补画后的图形为轴对称图形,并画出对称轴。
请你试一试
1
2
3
请你试一试
2.1图形的轴对称
1.定义:轴对称图形(折叠重合)
对称轴(直线)
对称点
折痕所在的直线就是轴对称图形的对称轴;
连结两个对称点之间的线段垂直平分线就是轴对称图形的对称轴
2.性质:对称轴垂直平分连结两个对称点的线段
3.性质:成轴对称的两个图形是全等图形
教学思考与反思
本节的重点是图形的轴对称的概念和性质,而轴对称图形谁学生在小学就已经建立起了一个感性的认识,课本上的概念也是通过折叠的方法来定义的,所以在教学中也是运用定义来判断。
数学教学要揭示数学知识的本质,不能仅凭感观认识来判断,我设计了一个试一试折叠折痕和不折叠找对称轴的环节,目的使学生从两方面认识对称轴:①折痕所在的直线是对称轴②连接两个对称点之间的线段垂直平分线是对称轴。继续运用课本中合作学习,通过对一个具有轴对称性的四边形的探索,让学生逐步认清轴对称图形的性质,对称轴垂直平分连结两个对称点线段。
对于课本例1的教学我思考很久,到底如何进行例1的教学,它起到什么作用?其实例1既是轴对称性质的运用,又是给出“两个图形成轴对称”概念。既然是轴对称图形性质的运用,一下子给出三个顶点和一个三角形这样复杂图形,恐学生一下子难以接受,我适时做个铺垫,先引入一个具有轴对称的四边形,找对称轴,再作四边形内一点的对称点,让学生运用性质思考和演示相结合,然后,让学生动手操作例1,再给出“两个图形成轴对称”概念。
新教材中不提轴对称变换,而改成写“这样的图形改变叫做图形的轴对称”,前面例1中引出的说法是“两个三角形关于直线成轴对称”这样显得概念太多,我认为学生对突如其来的这么多似是而非的概念会更为迷糊,所以我不提“这样的图形改变叫做图形的轴对称”,而是仍然延用“两个图形关于直线成轴对称”这一说法。显得简洁明了。
例2是我感觉尤为困惑,特难处理的一个环节,如同鸡肋,食之无味弃之可惜。尤其是其证明环节,很难理解,但它又是几何图形求最值的经典之作,不可舍不可弃。学习轴对称很大程度上也是为了求几何最值,如何把握这一经典之作,让学生能理解又记忆深刻呢?我采用先入为主,课前就提出这问题,将军饮马,求一折线和的最小值。让后通过对轴对称的学习,明确轴对称不改变大小但能改变图形方向,引导学生改变线段方向,将折线变形为另一“有可能三点共线的折线”,学生能理解到两点之间线段最短,我想就已经达到目的,至于课本中运用任意点情况的证明,这一方法实在是难以让学生接受。
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
