浙教版初中数学八年级上册 2.7 探索勾股定理 课件 (1)(17张)
文档属性
| 名称 | 浙教版初中数学八年级上册 2.7 探索勾股定理 课件 (1)(17张) |  | |
| 格式 | ppt | ||
| 文件大小 | 275.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-12 21:27:00 | ||
图片预览


文档简介
探索勾股定理
八年级数学(上册)?
1 在你的方格纸上作出两个直角三角形,使两直角边的长分别为:
(1)a=3 b=3 (4) a=3 b=4
2 分别以直角三角形各边为边长向外作正方形;
3 算出每一个正方形的面积
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
图1-1
图1-2
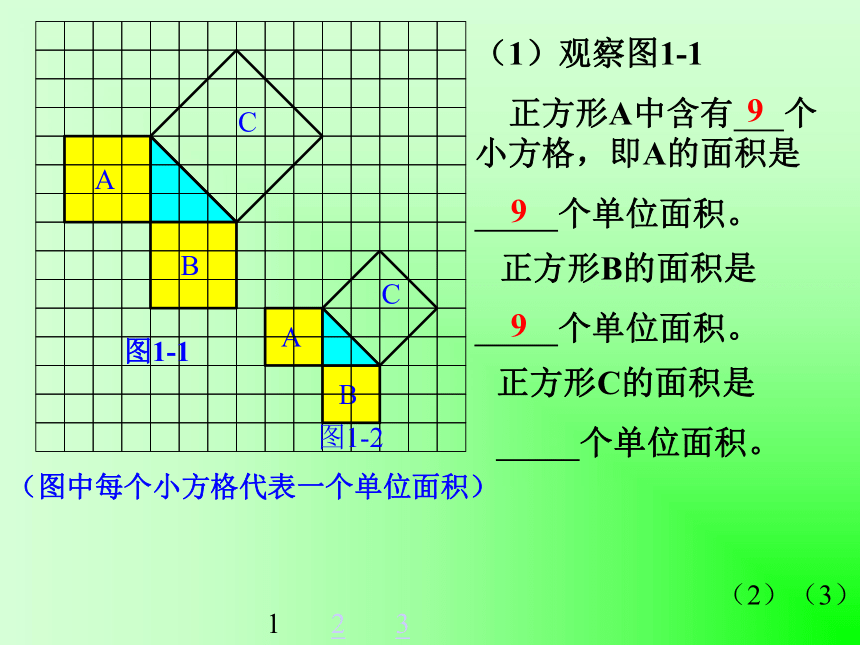
(1)观察图1-1
正方形A中含有 个小方格,即A的面积是
个单位面积。
正方形B的面积是
个单位面积。
正方形C的面积是
个单位面积。
9
9
9
1
2
3
(2)(3)
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
图1-1
图1-2
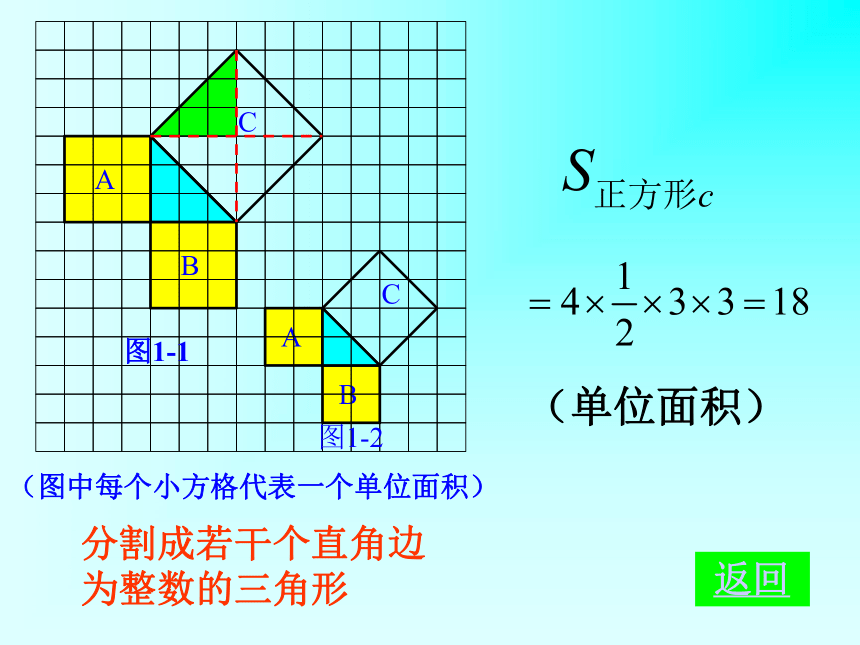
分割成若干个直角边为整数的三角形
(单位面积)
返回
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
图1-1
图1-2
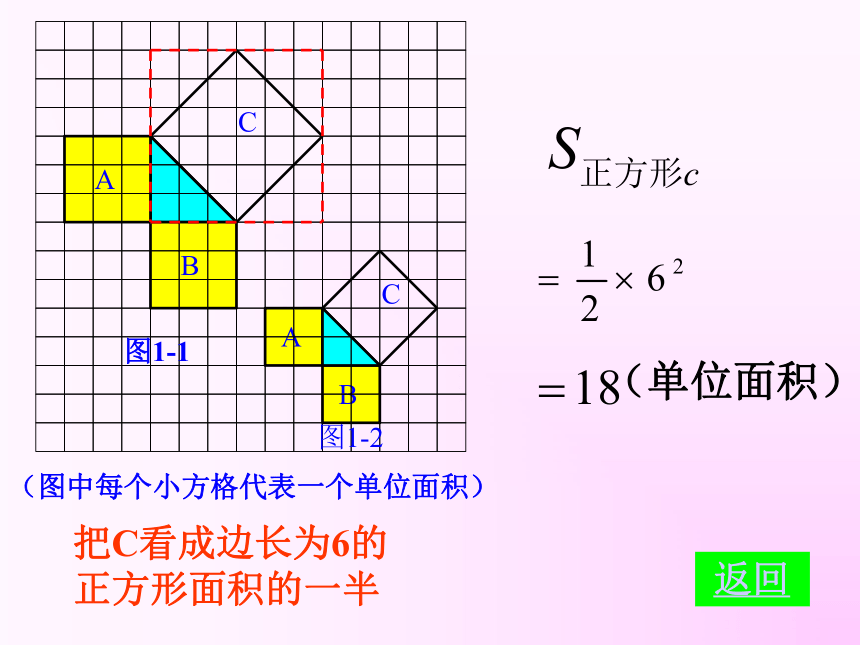
(单位面积)
把C看成边长为6的正方形面积的一半
返回
A
B
C
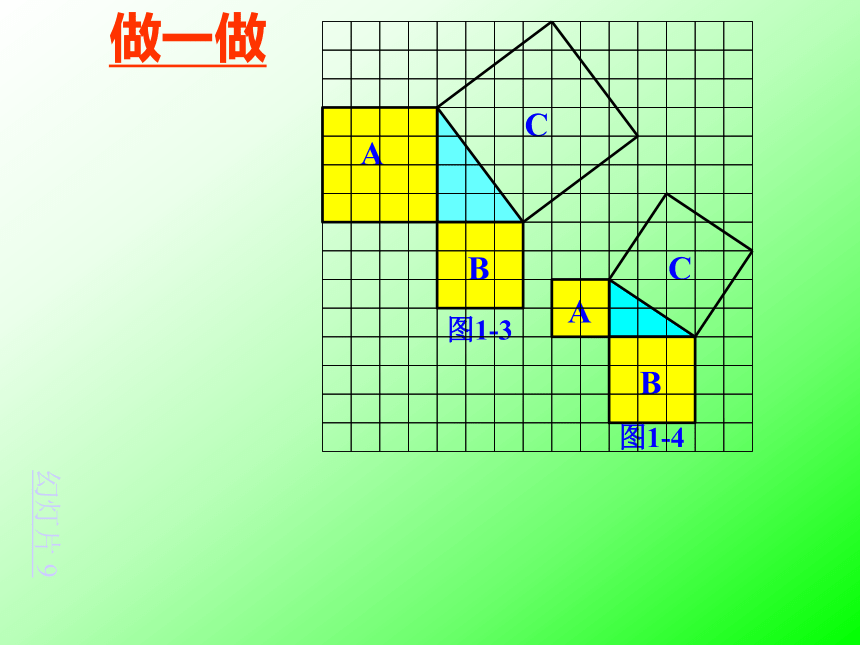
图1-3
A
B
C
图1-4
做一做
幻灯片 9
A
B
C
图1-3
A
B
C
图1-4
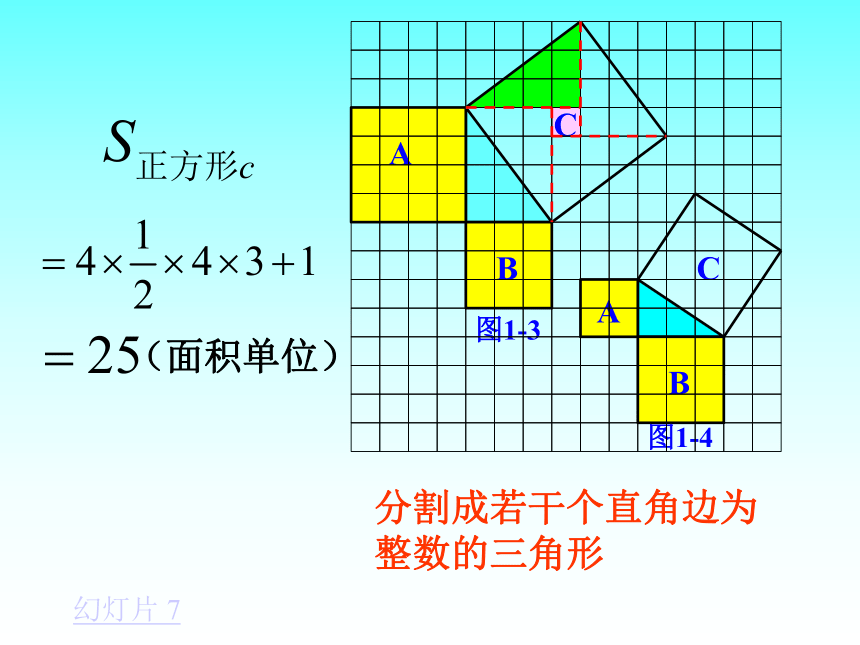
分割成若干个直角边为整数的三角形
(面积单位)
幻灯片 7
c
a
b
c
a
b
c
a
b
c
a
b
大正方形的面积可以表示为 ;
也可以表示为
c2
4?ab/2+(b- a)2
c
a
b
c
a
b
c
a
b
c
a
b
∵ (a+b)2 = c2 + 4?ab/2
a2+2ab+b2 = c2 +2ab
∴a2+b2=c2
大正方形的面积可以表示为 ;
也可以表示为
(a+b)2
c2 +4?ab/2
读一读
勾股世界
我国是最早了解勾股定理的国家之一。早在三千多年前,周朝数学家商高就提出,将一根直尺折成一个直角三角形,如果勾等于三,股等于四,那么弦就等于五。即“勾三、股四、弦五”。它被记载于我国古代著名的数学著作《周髀算经》中。在这本书中的另一处,还记载了勾股定理的一般形式。
1945年,人们在研究古巴比伦人遗留下的一块数学泥板时,惊讶地发现上面竟然刻有15组能构成直角三角形三边的数,其年代远在商高之前。
相传二千多年前,希腊的毕达哥拉斯学派首先证明了勾股定理,因此在国外人们通常称勾股定理为毕达哥拉斯定理。
(1)若a=1, b=2, 求c;
例1:已知ΔABC中,∠C=Rt∠,BC=a,
AC=b,AB=c。
(2)若a=15,c=17,求b;
(3)若c=34,a:b=8:15,求a、b;
练一练:
1、已知ΔABC中,∠C=Rt∠,BC=a,AC=b,AB=c。
(1)若 ,求c;
(2)若a=12,c=13,求b;
练一练:
2、求出图中直角三角形第三边的长度。
5
例2:如图,在△ABC中,AB=AC。已知AB=17,BC=16。
(1)求BC边上的中线AD的长。
(2)求△ABC的面积。
(3)过点B作BE⊥AC,垂足为E,求BE的长。
E
已知∠ACB=Rt∠,CD⊥AB,AC=3,BC=4.求CD的长.
练一练:
A
D
B
C
3
4
例3:一个长方形零件图,根据所给的尺寸
(单位mm),求两孔中心A、B之间的距离.
A
B
90
160
40
40
C
2、在数轴上画出表示 的点。
合作学习:
A
1
1
1、数轴上点A表示的数是什么?
八年级数学(上册)?
1 在你的方格纸上作出两个直角三角形,使两直角边的长分别为:
(1)a=3 b=3 (4) a=3 b=4
2 分别以直角三角形各边为边长向外作正方形;
3 算出每一个正方形的面积
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
图1-1
图1-2
(1)观察图1-1
正方形A中含有 个小方格,即A的面积是
个单位面积。
正方形B的面积是
个单位面积。
正方形C的面积是
个单位面积。
9
9
9
1
2
3
(2)(3)
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
图1-1
图1-2
分割成若干个直角边为整数的三角形
(单位面积)
返回
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
图1-1
图1-2
(单位面积)
把C看成边长为6的正方形面积的一半
返回
A
B
C
图1-3
A
B
C
图1-4
做一做
幻灯片 9
A
B
C
图1-3
A
B
C
图1-4
分割成若干个直角边为整数的三角形
(面积单位)
幻灯片 7
c
a
b
c
a
b
c
a
b
c
a
b
大正方形的面积可以表示为 ;
也可以表示为
c2
4?ab/2+(b- a)2
c
a
b
c
a
b
c
a
b
c
a
b
∵ (a+b)2 = c2 + 4?ab/2
a2+2ab+b2 = c2 +2ab
∴a2+b2=c2
大正方形的面积可以表示为 ;
也可以表示为
(a+b)2
c2 +4?ab/2
读一读
勾股世界
我国是最早了解勾股定理的国家之一。早在三千多年前,周朝数学家商高就提出,将一根直尺折成一个直角三角形,如果勾等于三,股等于四,那么弦就等于五。即“勾三、股四、弦五”。它被记载于我国古代著名的数学著作《周髀算经》中。在这本书中的另一处,还记载了勾股定理的一般形式。
1945年,人们在研究古巴比伦人遗留下的一块数学泥板时,惊讶地发现上面竟然刻有15组能构成直角三角形三边的数,其年代远在商高之前。
相传二千多年前,希腊的毕达哥拉斯学派首先证明了勾股定理,因此在国外人们通常称勾股定理为毕达哥拉斯定理。
(1)若a=1, b=2, 求c;
例1:已知ΔABC中,∠C=Rt∠,BC=a,
AC=b,AB=c。
(2)若a=15,c=17,求b;
(3)若c=34,a:b=8:15,求a、b;
练一练:
1、已知ΔABC中,∠C=Rt∠,BC=a,AC=b,AB=c。
(1)若 ,求c;
(2)若a=12,c=13,求b;
练一练:
2、求出图中直角三角形第三边的长度。
5
例2:如图,在△ABC中,AB=AC。已知AB=17,BC=16。
(1)求BC边上的中线AD的长。
(2)求△ABC的面积。
(3)过点B作BE⊥AC,垂足为E,求BE的长。
E
已知∠ACB=Rt∠,CD⊥AB,AC=3,BC=4.求CD的长.
练一练:
A
D
B
C
3
4
例3:一个长方形零件图,根据所给的尺寸
(单位mm),求两孔中心A、B之间的距离.
A
B
90
160
40
40
C
2、在数轴上画出表示 的点。
合作学习:
A
1
1
1、数轴上点A表示的数是什么?
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
