浙教版初中数学八年级上册 2.7 探索勾股定理 课件(21张)
文档属性
| 名称 | 浙教版初中数学八年级上册 2.7 探索勾股定理 课件(21张) |
|
|
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-12 19:38:47 | ||
图片预览




文档简介
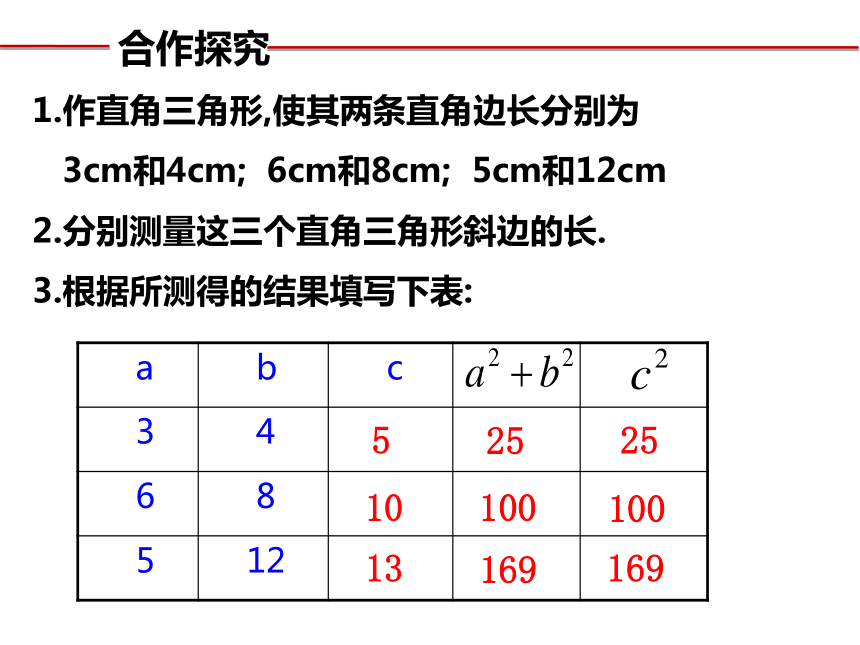
印度数学家什迦逻(1141年-1225年?)
曾提出过“荷花问题”:
平平湖水清可鉴,面上半尺生红莲;
出泥不染亭亭立,忽被强风吹一边,
渔人观看忙向前,花离原位二尺远;
能算诸君请解题,湖水如何知深浅?
x
2
x+0.5
0.5
C
A
B
挑战数学家
2.7探索勾股定理(1)
今日课题
合作探究
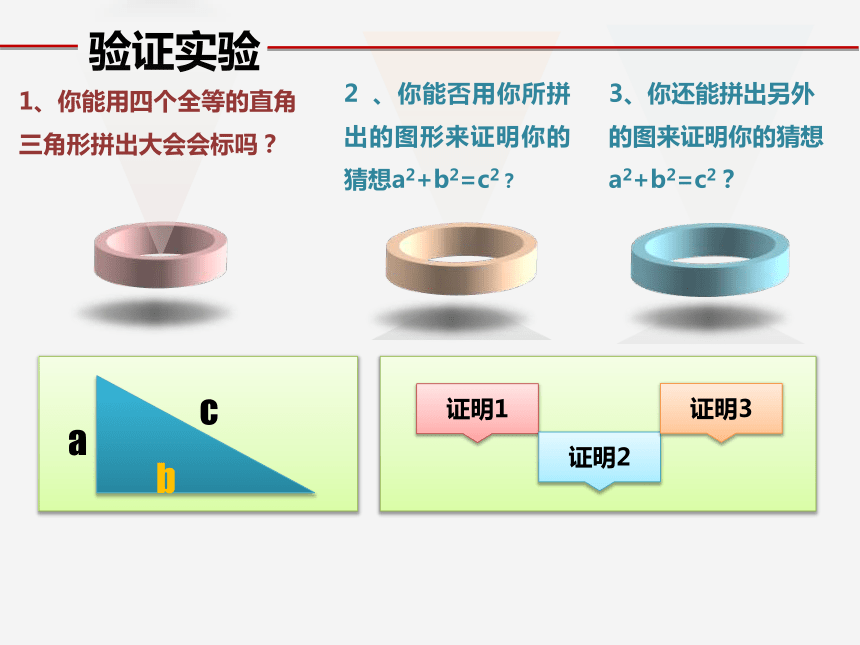
1.作直角三角形,使其两条直角边长分别为
3cm和4cm; 6cm和8cm; 5cm和12cm
2.分别测量这三个直角三角形斜边的长.
3.根据所测得的结果填写下表:
a
b
c
3
4
6
8
5
12
5
25
25
10
100
100
13
169
169
发现规律
如果a、b为直角三角形的两条直角边长, c为斜边长,那么
a
b
c
即:直角三角形两直角边的平方和等于斜边的平方。
2002年世界数学家大会会标
该图2002年8月在北京召开的国际数学家大会的会标示意图,它的设计思路可以追溯到3世纪中国数学家赵爽所使用的弦图。用弦图证明勾股定理在数学史上有着重要的地位。
效仿先贤
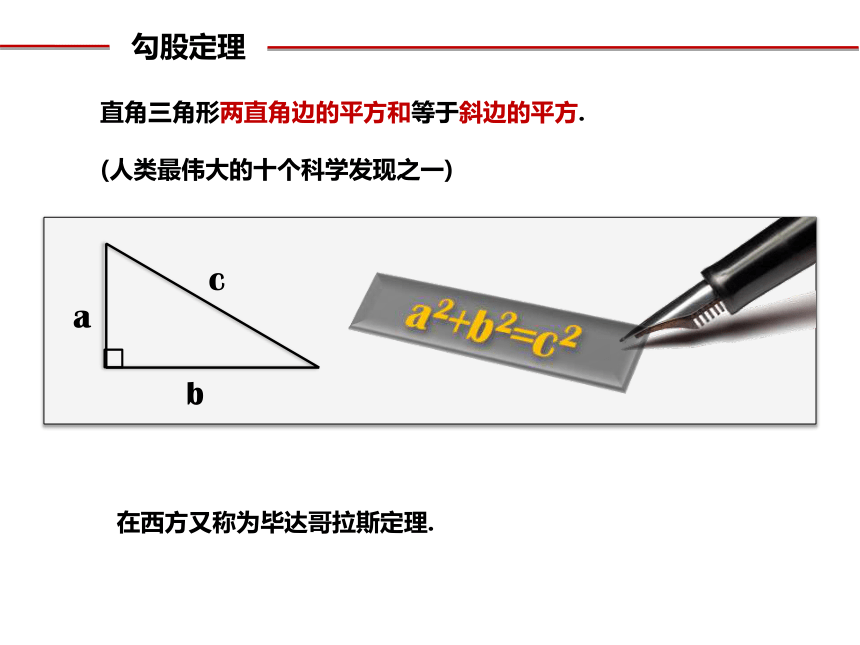
验证实验
2 、你能否用你所拼出的图形来证明你的猜想a2+b2=c2?
3、你还能拼出另外的图来证明你的猜想a2+b2=c2?
1、你能用四个全等的直角三角形拼出大会会标吗?
c
a
b
证明1
证明2
证明3
c
a
b
c
a
b
c
a
b
c
a
b
∵ c2=
=b2-2ab+a2+ 2ab
=a2+b2
∴a2+b2=c2
大正方形的面积可以表示为 ;
也可以表示为 。
c2
1
(b-a)2+4×
2
ab
1
(b-a)2+4×
2
ab
证明1
证明2
c
a
b
c
a
b
c
a
b
c
a
b
∵ (a+b)2 =
a2+2ab+b2 = 2ab +c2
∴a2+b2=c2
大正方形的面积可以表示为 ;
也可以表示为 。
(a+b)2
1
4×
2
ab+c2
1
4×
2
ab+c2
证明3
只用这两个直角三角形来证明
a
b
c
a
c
b
A
B
C
D
E
又∵S梯形ABCD=S△AED+S△EBC+S△CED
∴比较上面二式得c2=a2+b2
∵S梯形ABCD=
1
2
(a+b)2
=
1
2
(a2+2ab+b2)
=
1
2
ab+
1
2
ba+
1
2
c2
=
1
2
(2ab+c2)
勾股定理
直角三角形两直角边的平方和等于斜边的平方.
(人类最伟大的十个科学发现之一)
a
b
c
a2+b2=c2
在西方又称为毕达哥拉斯定理.
勾2+股2=弦2
辉煌发现
我国早在三千多年就知道了这个定理,人们把弯曲成直角的手臂的上半部分称为“勾”,下半部分称为“股”,我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”。因此就把这一定理称为勾股定理。
勾
股
勾
股
弦
定理理解
判断题:
(1).如果三角形的三边长分别为a,b,c,则
( )
(2).如果直角三角形的三边长分别为a,b,c,
( )
则
X
X
c2=a2 + b2
a
b
c
b2 =c2 -a2
a2=c2 - b2
定理变形
直角三角形中,两直角边的平方和等于斜边的平方
定理应用
例1、已知△ABC中, ∠C=Rt∠,BC=a,AC=b,AB=C
已知: a=1, b=2, 求c;
(2)已知: a=15, c=17, 求b;
(3)已知:c=34, a:b=8:15, 求a, b.
思考:
如何利用直角三角形在数轴上表示点 ?
0
2
1
A
B
C
拓展提高
变式一:已知Rt△ABC中,∠B=90°,AB=c,BC=a,AC=b.如果 a=1, b=2, 求c;
c=?
b=2
a=1
b=2
a=1
变式二:已知Rt△ABC中,AB=c,BC=a,AC=b.如果a=1, b=2, 求c;
c=?
例2、如图:是一个长方形零件图,根据所给的尺寸(单位:mm),求两孔中心A、B之间的距离。
A
B
C
40
90
160
40
解:过A作铅垂线,过B作水平线,两线交于点C,则∠C =90。
AC=90-40=50(mm),
BC=160-40=120(mm).
∵ ∠C =90。
∴ AB2=AC2+BC2
∵AB>0
∴AB=130(mm)
答:两孔中心A,B之间的距离为130mm.
=502+1202
=16900(mm2)
学以致用
1、在Rt△ABC中,∠C=90°,
①若a= , b= ,则c= ;②若a=15,c=25,则b= ;
③若c=61,b=60,则a= ;
④若a∶b=3∶4,c=10则S△ABC= 。
2、如图,厂房屋顶的人字架是
等腰三角形,若跨度 BC=16米,
上弦长AB=10米,则中柱AD= 米,
面积是 米2
1
20
11
24
6
48
课堂小结
定理内容
定理应用
数形结合的思想
从一般到特殊的数学思想
印度数学家什迦逻(1141年-1225年?)
曾提出过“荷花问题”:
“平平湖水清可鉴,面上半尺生红莲;
出泥不染亭亭立,忽被强风吹一边,
渔人观看忙向前,花离原位二尺远;
能算诸君请解题,湖水如何知深浅?”
x
2
x+0.5
0.5
C
A
B
挑战数学家
课后小实验
如图,分别以直角三角形的三边为边长作三个正方形,
这三个正方形的面积之间有什么关系?为什么?
1
2
如图,分别以直角三角形的三边为直径作三个半圆,这三个半圆的面积之间有什么关系?为什么?
如图,分别以直角三角形的三边为边长作三个等边三角形,
这三个等边三角形的面积之间有什么关系?为什么?
3
A
B
C
教师寄语
要养成用数学的思维去解读世界的习惯。
只有不断的思考,才会有新的发现;只有量的变化,才会有质的进步。
其实数学在我们的生活中无处不在, 只要你是个有心人,就一定会发现在我们的身边,我们的眼前, 还有很多象 “勾股定理”那样的知识等待我们去探索,等待我们去发现……
曾提出过“荷花问题”:
平平湖水清可鉴,面上半尺生红莲;
出泥不染亭亭立,忽被强风吹一边,
渔人观看忙向前,花离原位二尺远;
能算诸君请解题,湖水如何知深浅?
x
2
x+0.5
0.5
C
A
B
挑战数学家
2.7探索勾股定理(1)
今日课题
合作探究
1.作直角三角形,使其两条直角边长分别为
3cm和4cm; 6cm和8cm; 5cm和12cm
2.分别测量这三个直角三角形斜边的长.
3.根据所测得的结果填写下表:
a
b
c
3
4
6
8
5
12
5
25
25
10
100
100
13
169
169
发现规律
如果a、b为直角三角形的两条直角边长, c为斜边长,那么
a
b
c
即:直角三角形两直角边的平方和等于斜边的平方。
2002年世界数学家大会会标
该图2002年8月在北京召开的国际数学家大会的会标示意图,它的设计思路可以追溯到3世纪中国数学家赵爽所使用的弦图。用弦图证明勾股定理在数学史上有着重要的地位。
效仿先贤
验证实验
2 、你能否用你所拼出的图形来证明你的猜想a2+b2=c2?
3、你还能拼出另外的图来证明你的猜想a2+b2=c2?
1、你能用四个全等的直角三角形拼出大会会标吗?
c
a
b
证明1
证明2
证明3
c
a
b
c
a
b
c
a
b
c
a
b
∵ c2=
=b2-2ab+a2+ 2ab
=a2+b2
∴a2+b2=c2
大正方形的面积可以表示为 ;
也可以表示为 。
c2
1
(b-a)2+4×
2
ab
1
(b-a)2+4×
2
ab
证明1
证明2
c
a
b
c
a
b
c
a
b
c
a
b
∵ (a+b)2 =
a2+2ab+b2 = 2ab +c2
∴a2+b2=c2
大正方形的面积可以表示为 ;
也可以表示为 。
(a+b)2
1
4×
2
ab+c2
1
4×
2
ab+c2
证明3
只用这两个直角三角形来证明
a
b
c
a
c
b
A
B
C
D
E
又∵S梯形ABCD=S△AED+S△EBC+S△CED
∴比较上面二式得c2=a2+b2
∵S梯形ABCD=
1
2
(a+b)2
=
1
2
(a2+2ab+b2)
=
1
2
ab+
1
2
ba+
1
2
c2
=
1
2
(2ab+c2)
勾股定理
直角三角形两直角边的平方和等于斜边的平方.
(人类最伟大的十个科学发现之一)
a
b
c
a2+b2=c2
在西方又称为毕达哥拉斯定理.
勾2+股2=弦2
辉煌发现
我国早在三千多年就知道了这个定理,人们把弯曲成直角的手臂的上半部分称为“勾”,下半部分称为“股”,我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”。因此就把这一定理称为勾股定理。
勾
股
勾
股
弦
定理理解
判断题:
(1).如果三角形的三边长分别为a,b,c,则
( )
(2).如果直角三角形的三边长分别为a,b,c,
( )
则
X
X
c2=a2 + b2
a
b
c
b2 =c2 -a2
a2=c2 - b2
定理变形
直角三角形中,两直角边的平方和等于斜边的平方
定理应用
例1、已知△ABC中, ∠C=Rt∠,BC=a,AC=b,AB=C
已知: a=1, b=2, 求c;
(2)已知: a=15, c=17, 求b;
(3)已知:c=34, a:b=8:15, 求a, b.
思考:
如何利用直角三角形在数轴上表示点 ?
0
2
1
A
B
C
拓展提高
变式一:已知Rt△ABC中,∠B=90°,AB=c,BC=a,AC=b.如果 a=1, b=2, 求c;
c=?
b=2
a=1
b=2
a=1
变式二:已知Rt△ABC中,AB=c,BC=a,AC=b.如果a=1, b=2, 求c;
c=?
例2、如图:是一个长方形零件图,根据所给的尺寸(单位:mm),求两孔中心A、B之间的距离。
A
B
C
40
90
160
40
解:过A作铅垂线,过B作水平线,两线交于点C,则∠C =90。
AC=90-40=50(mm),
BC=160-40=120(mm).
∵ ∠C =90。
∴ AB2=AC2+BC2
∵AB>0
∴AB=130(mm)
答:两孔中心A,B之间的距离为130mm.
=502+1202
=16900(mm2)
学以致用
1、在Rt△ABC中,∠C=90°,
①若a= , b= ,则c= ;②若a=15,c=25,则b= ;
③若c=61,b=60,则a= ;
④若a∶b=3∶4,c=10则S△ABC= 。
2、如图,厂房屋顶的人字架是
等腰三角形,若跨度 BC=16米,
上弦长AB=10米,则中柱AD= 米,
面积是 米2
1
20
11
24
6
48
课堂小结
定理内容
定理应用
数形结合的思想
从一般到特殊的数学思想
印度数学家什迦逻(1141年-1225年?)
曾提出过“荷花问题”:
“平平湖水清可鉴,面上半尺生红莲;
出泥不染亭亭立,忽被强风吹一边,
渔人观看忙向前,花离原位二尺远;
能算诸君请解题,湖水如何知深浅?”
x
2
x+0.5
0.5
C
A
B
挑战数学家
课后小实验
如图,分别以直角三角形的三边为边长作三个正方形,
这三个正方形的面积之间有什么关系?为什么?
1
2
如图,分别以直角三角形的三边为直径作三个半圆,这三个半圆的面积之间有什么关系?为什么?
如图,分别以直角三角形的三边为边长作三个等边三角形,
这三个等边三角形的面积之间有什么关系?为什么?
3
A
B
C
教师寄语
要养成用数学的思维去解读世界的习惯。
只有不断的思考,才会有新的发现;只有量的变化,才会有质的进步。
其实数学在我们的生活中无处不在, 只要你是个有心人,就一定会发现在我们的身边,我们的眼前, 还有很多象 “勾股定理”那样的知识等待我们去探索,等待我们去发现……
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
