浙教版初中数学八年级上册2.7 探索勾股定理 课件(共21张ppt)
文档属性
| 名称 | 浙教版初中数学八年级上册2.7 探索勾股定理 课件(共21张ppt) | 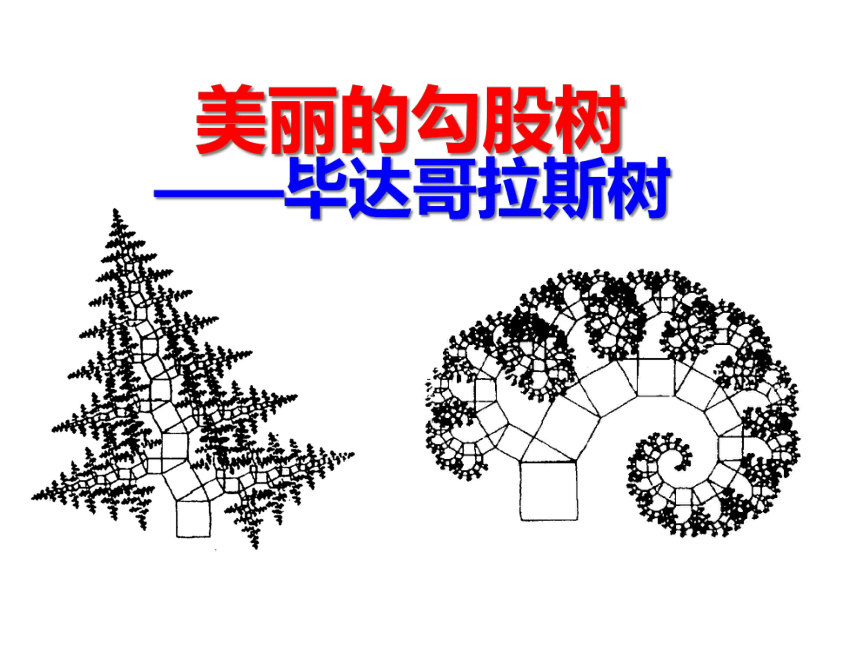 | |
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-12 21:32:05 | ||
图片预览




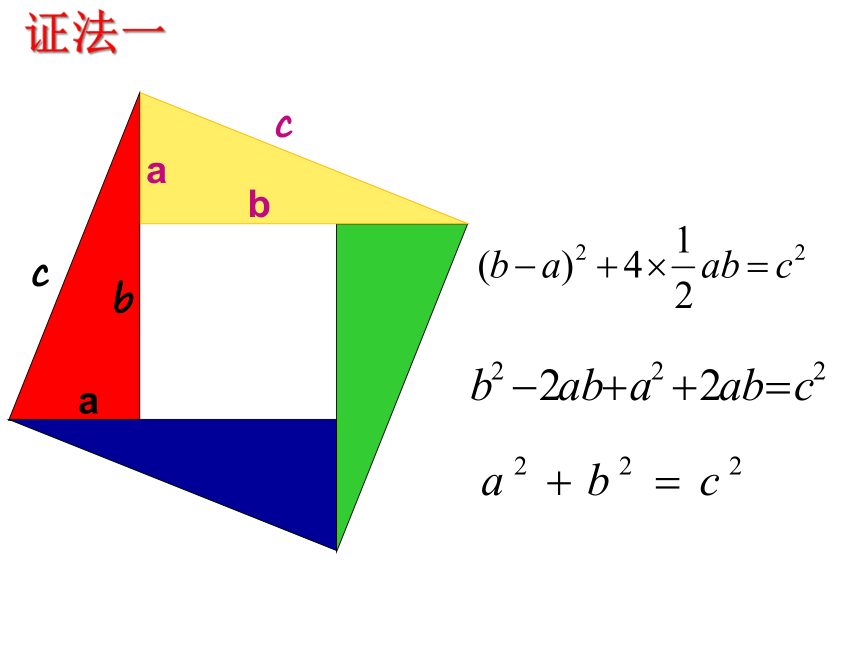
文档简介
美丽的勾股树
——毕达哥拉斯树
A
B
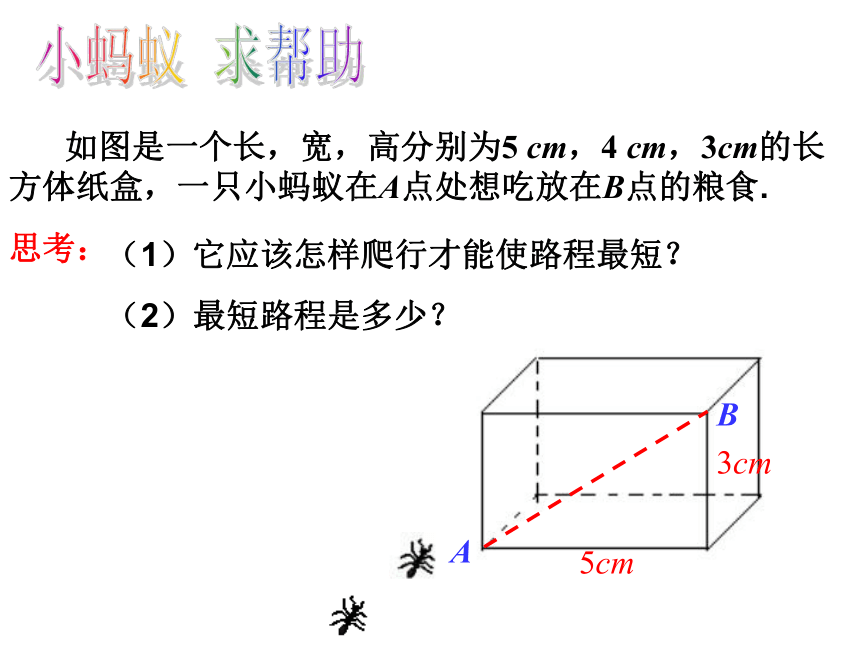
小蚂蚁 求帮助
如图是一个长,宽,高分别为5 cm,4 cm,3cm的长方体纸盒,一只小蚂蚁在A点处想吃放在B点的粮食.
(1)它应该怎样爬行才能使路程最短?
思考:
(2)最短路程是多少?
5cm
3cm
2.7探索勾股定理
西周开国时期(约公元前1000多年)
商高发现勾三股四弦五
2500多年前(约公元前500多年)
毕达哥拉斯在朋友家地板上发现
直角三角形三边的特殊关系.
东汉末至三国时代(约222年)
赵爽画出弦图验证勾股定理
勾股史话
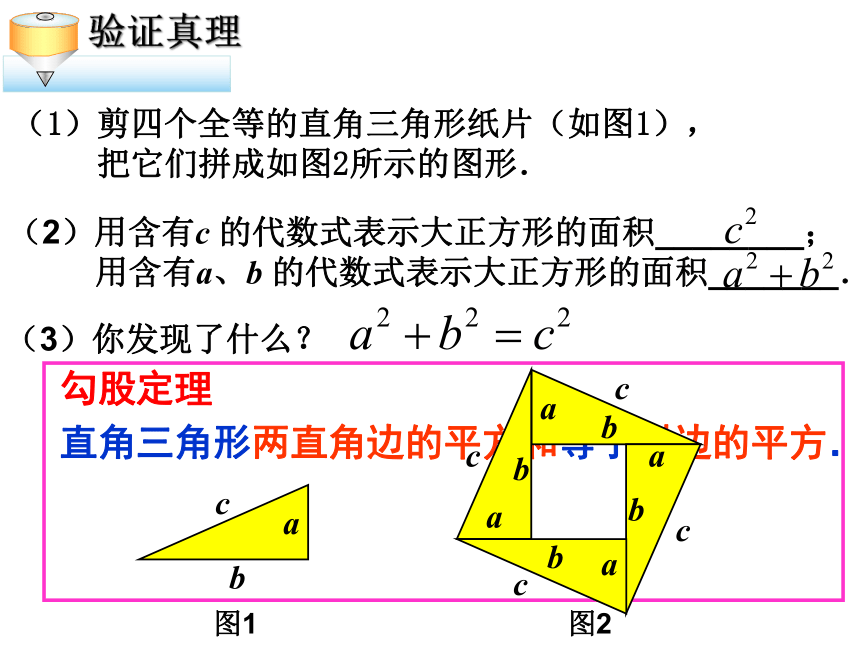
(1)剪四个全等的直角三角形纸片(如图1),
把它们拼成如图2所示的图形.
(2)用含有c 的代数式表示大正方形的面积________;
用含有a、b 的代数式表示大正方形的面积_______.
(3)你发现了什么?
验证真理
直角三角形两直角边的平方和等于斜边的平方.
勾股定理
c
c
c
c
a
a
a
a
b
b
b
b
图2
a
b
c
图1
a
c
b
a
b
c
证法一
a
b
c
a
b
c
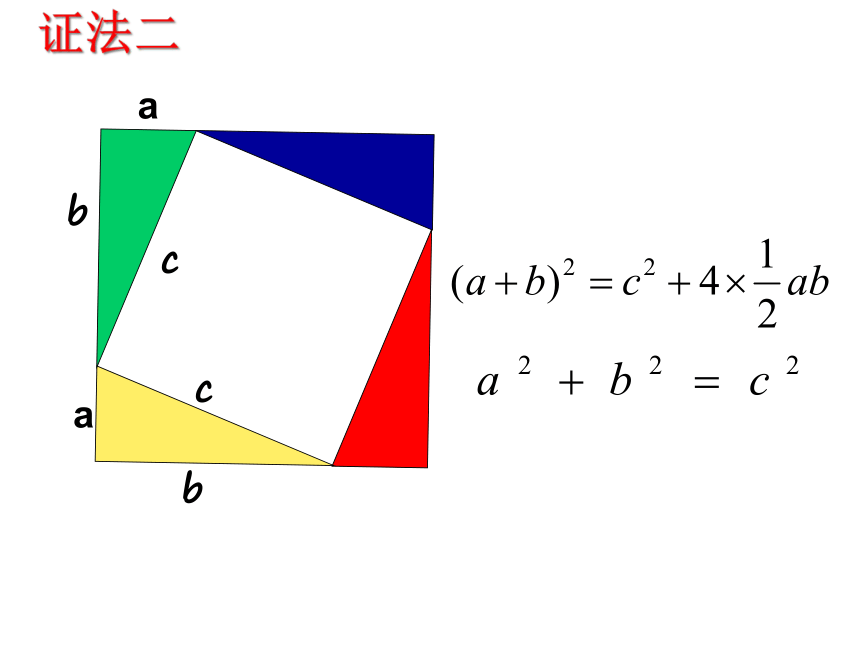
证法二
a
b
c
a
b
c
=
=
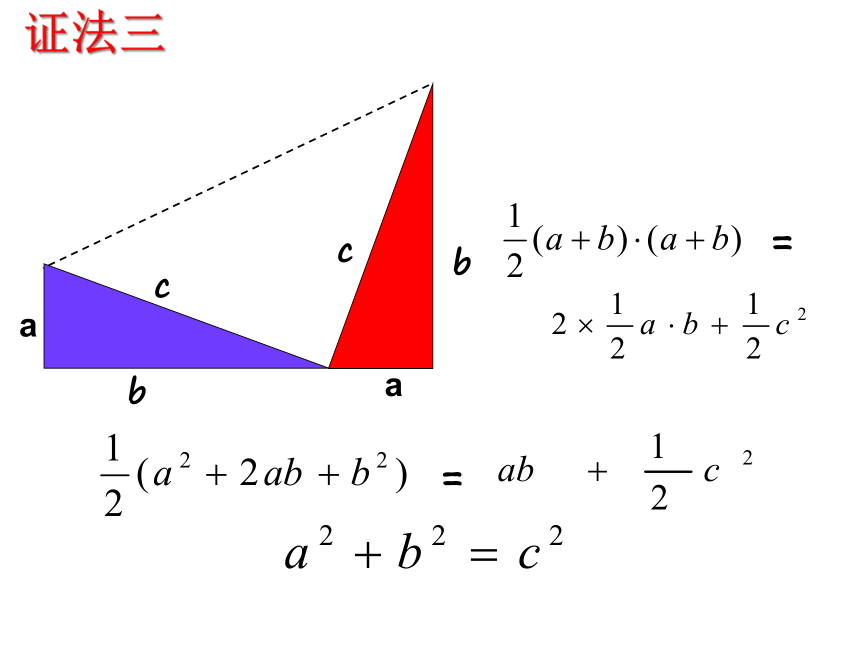
证法三
勾股定理
直角三角形两条直角边的平方
和等于斜边的平方.
∴ a2+b2=c2
在Rt△ABC中
∵ ∠C=Rt∠
(AC2+BC2=AB2)
勾
股
弦
c
a
a
a
a
b
b
b
b
c
c
c
总统证法
a
a
b
b
c
c
例1:
已知在△ABC中,∠C=90°,BC=a,AC=b,AB=c.
(1)a=1,b=2,求c
(2)a=1,c =2,求b
a
c
b
A
B
C
运用真理
(3)若c=34,a:b=8:15,求a、b;
试一试
1、在△ABC中,∠C= .
(1)若a=5,b=12,则c= .
(2)若c=4,b= ,则a= .
2、已知△ABC的三边分别是a,b,c,
若∠B=Rt∠,则有关系式( )
A.a2+b2=c2
B.a2+c2=b2
C.a2-b2=c2
D.b2+c2=a2
练一练一:
求出图中直角三角形第三边的长度。
5
印度数学家什迦逻(1141年-1225年?)
曾提出过“荷花问题”:
“平平湖水清可鉴,面上半尺生红莲;
出泥不染亭亭立,忽被强风吹一边,
渔人观看忙向前,花离原位二尺远;
能算诸君请解题,湖水如何知深浅?”
2
0.5
C
A
B
你会算吗?
D
变式1:
已知直角三角形的两边长分别是2cm和3cm,则第三边的长度为_______.
变式2:
用三角尺和圆规,作一条线段,使它的长度为 cm.
运用真理
读清题意,注意分类讨论
如何构造直角三角形是关键,数形结合思想很重要
在数轴上画出表示 的点。
A
1
1
数轴上点A表示的数是什么?
练一练二:
0
例2:
如图是一个长方形零件图.根据所给尺寸(单位:mm),求两孔中心A,B之间的距离.
构造直角三角形很关键,已知两边求第三边你会了吗?
运用真理
c
小结
体会.分享
1.什么是勾股定理?
2.学习勾股定理有什么用处?
考考你
2、 已知直角三角形的两边长分别
是6cm和8cm,则这个直角三角形
的面积为_______
1、已知三角形三边分别为5、5、6,三角形的面积为_______.
3、边长为10的正三角形面积为_________
a
能力提升
A
C
一只小蜜蜂在纸盒内部的A点处想去放在C点的花处采蜜,它飞行
的最短路程是_________cm.
如图是一个长,宽,高分别为5cm,4 cm,3cm的长方体纸盒.
——毕达哥拉斯树
A
B
小蚂蚁 求帮助
如图是一个长,宽,高分别为5 cm,4 cm,3cm的长方体纸盒,一只小蚂蚁在A点处想吃放在B点的粮食.
(1)它应该怎样爬行才能使路程最短?
思考:
(2)最短路程是多少?
5cm
3cm
2.7探索勾股定理
西周开国时期(约公元前1000多年)
商高发现勾三股四弦五
2500多年前(约公元前500多年)
毕达哥拉斯在朋友家地板上发现
直角三角形三边的特殊关系.
东汉末至三国时代(约222年)
赵爽画出弦图验证勾股定理
勾股史话
(1)剪四个全等的直角三角形纸片(如图1),
把它们拼成如图2所示的图形.
(2)用含有c 的代数式表示大正方形的面积________;
用含有a、b 的代数式表示大正方形的面积_______.
(3)你发现了什么?
验证真理
直角三角形两直角边的平方和等于斜边的平方.
勾股定理
c
c
c
c
a
a
a
a
b
b
b
b
图2
a
b
c
图1
a
c
b
a
b
c
证法一
a
b
c
a
b
c
证法二
a
b
c
a
b
c
=
=
证法三
勾股定理
直角三角形两条直角边的平方
和等于斜边的平方.
∴ a2+b2=c2
在Rt△ABC中
∵ ∠C=Rt∠
(AC2+BC2=AB2)
勾
股
弦
c
a
a
a
a
b
b
b
b
c
c
c
总统证法
a
a
b
b
c
c
例1:
已知在△ABC中,∠C=90°,BC=a,AC=b,AB=c.
(1)a=1,b=2,求c
(2)a=1,c =2,求b
a
c
b
A
B
C
运用真理
(3)若c=34,a:b=8:15,求a、b;
试一试
1、在△ABC中,∠C= .
(1)若a=5,b=12,则c= .
(2)若c=4,b= ,则a= .
2、已知△ABC的三边分别是a,b,c,
若∠B=Rt∠,则有关系式( )
A.a2+b2=c2
B.a2+c2=b2
C.a2-b2=c2
D.b2+c2=a2
练一练一:
求出图中直角三角形第三边的长度。
5
印度数学家什迦逻(1141年-1225年?)
曾提出过“荷花问题”:
“平平湖水清可鉴,面上半尺生红莲;
出泥不染亭亭立,忽被强风吹一边,
渔人观看忙向前,花离原位二尺远;
能算诸君请解题,湖水如何知深浅?”
2
0.5
C
A
B
你会算吗?
D
变式1:
已知直角三角形的两边长分别是2cm和3cm,则第三边的长度为_______.
变式2:
用三角尺和圆规,作一条线段,使它的长度为 cm.
运用真理
读清题意,注意分类讨论
如何构造直角三角形是关键,数形结合思想很重要
在数轴上画出表示 的点。
A
1
1
数轴上点A表示的数是什么?
练一练二:
0
例2:
如图是一个长方形零件图.根据所给尺寸(单位:mm),求两孔中心A,B之间的距离.
构造直角三角形很关键,已知两边求第三边你会了吗?
运用真理
c
小结
体会.分享
1.什么是勾股定理?
2.学习勾股定理有什么用处?
考考你
2、 已知直角三角形的两边长分别
是6cm和8cm,则这个直角三角形
的面积为_______
1、已知三角形三边分别为5、5、6,三角形的面积为_______.
3、边长为10的正三角形面积为_________
a
能力提升
A
C
一只小蜜蜂在纸盒内部的A点处想去放在C点的花处采蜜,它飞行
的最短路程是_________cm.
如图是一个长,宽,高分别为5cm,4 cm,3cm的长方体纸盒.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
