浙教版初中数学九年级上册 1.2 二次函数图像 课件 (2)(11张)
文档属性
| 名称 | 浙教版初中数学九年级上册 1.2 二次函数图像 课件 (2)(11张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-12 21:34:19 | ||
图片预览


文档简介
二次函数图象与性质复习
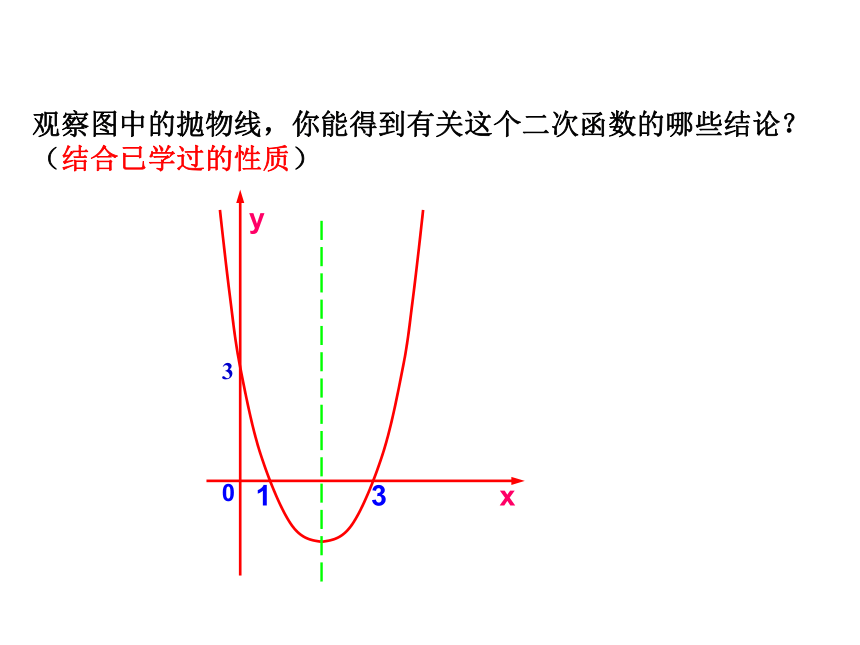
观察图中的抛物线,你能得到有关这个二次函数的哪些结论?(结合已学过的性质)
1
3
3
0
x
y
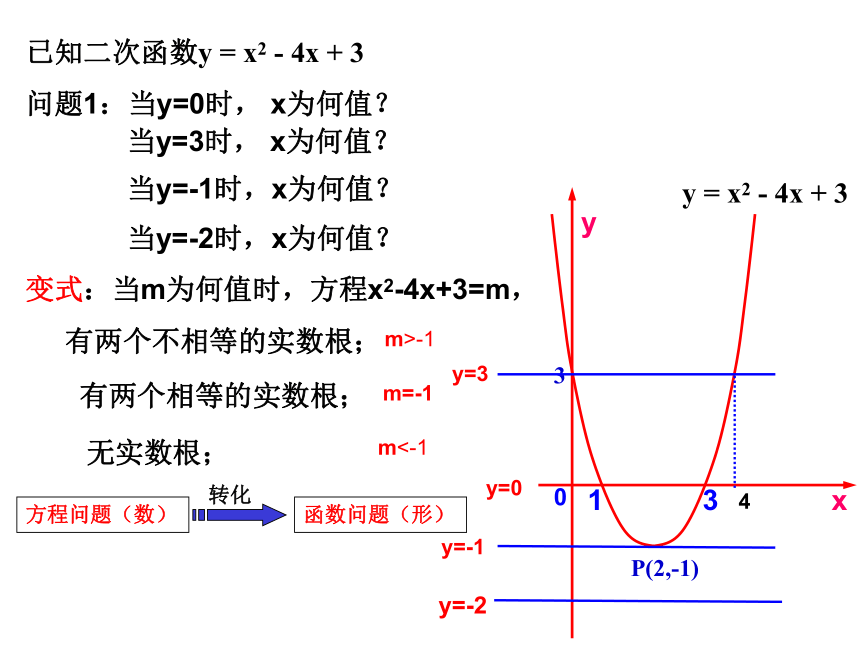
已知二次函数y = x2 - 4x + 3
问题1:当y=0时, x为何值?
当y=3时, x为何值?
当y=-1时,x为何值?
变式:当m为何值时,方程x2-4x+3=m,
有两个不相等的实数根;
1
3
3
0
x
y
方程问题(数)
转化
函数问题(形)
有两个相等的实数根;
无实数根;
m>-1
m=-1
m<-1
当y=-2时,x为何值?
y=0
P(2,-1)
y=3
y=-1
y=-2
4
y = x2 - 4x + 3
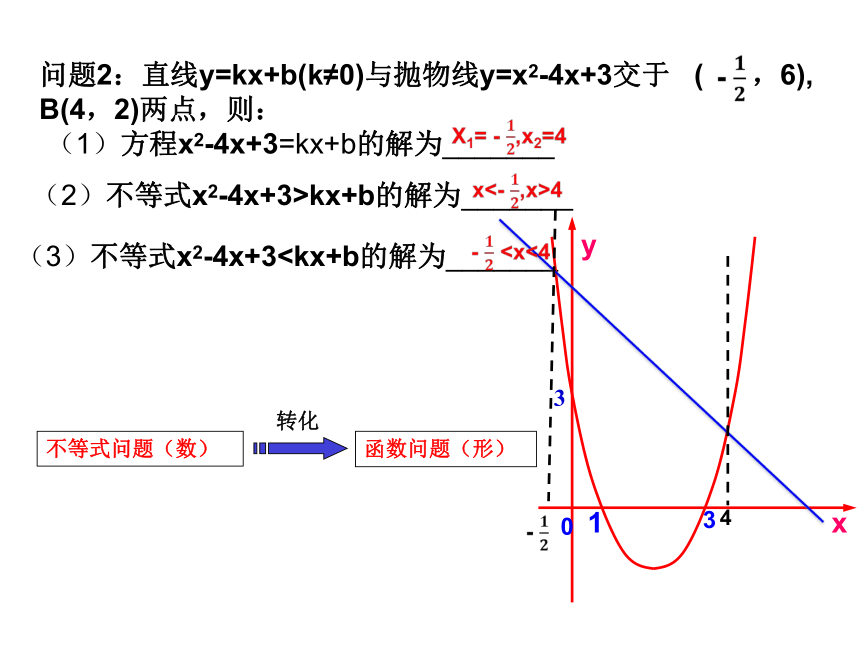
(2)不等式x2-4x+3>kx+b的解为_______
(3)不等式x2-4x+31
3
3
0
x
y
4
不等式问题(数)
转化
函数问题(形)
?
?
?
问题2:直线y=kx+b(k≠0)与抛物线y=x2-4x+3交于 ( ,6),
B(4,2)两点,则:
(1)方程x2-4x+3=kx+b的解为_______
?
?
P(2,-1)
问题3:如图,已知二次函数y = x2 - 4x + 3,P为顶点,B(3,0),C(0,3)
(1)求△ PBC的面积。
1
3
3
0
x
y
y=x2-4x+3
A
B
C
问题3:(2)点Q是抛物线y=x2-4x+3(1< x <3)上的一个动点。 Q的横坐标为m, 若△QBC的面积为s,求出s关于m的函数关系式。
(3)当m取何值时, S的面积最大,最大面积为多少?
1
3
3
0
x
y
y=x2-4x+3
A
B
C
Q
x
y
o
y = x2 - 4x + 3
A(1,0)
B(3,0)
C(0,3)
P(2,-1)
直线x=2
M
问题4:对称轴上是否存在点M,
使△AMC周长最小?若存在请你
求出点M的坐标;
若不存在请说明理由。
M
x
y
o
A(1,0)
B(3,0)
C(0,3)
P(2,-1)
直线x=2
G
问题4:对称轴上是否存在点M,
使△AMC周长最小?若存在请你
求出点M的坐标;
若不存在请说明理由。
y = x2 - 4x + 3
分享收获
思想方法
数形结合思想(用数表达,用形释义)
数缺形时少直观,形缺数时难入微,
两者结合万般好,隔离分家万事休 。
——华罗庚
小结
回顾与反思
?
二次函数的解析式
名称
顶点式
一般式
交点式
二次函数解析式
对称轴
顶点坐标
增减性
a>0
a<0
最值
a>0
a<0
y=a(x+m)2+k
y=ax2+bx+c
y=a(x-x1)(x-x2)
直线x=-m
直线x=
直线x=
(-m,k)
( )
当x≤-m时,y随x的增大而减小;当x≥-m时,y随x的增大而增大
当x ≤ 时,y随x的增大而减小;当x ≥ 时y随x的增大而增大
当x≤-m时,y随的增大而增大;当x≥-m时,y随的增大而减小
当x≤ 时,y随x的增大而增大;当x≥ 时y随x的增大而减小
当 x=-m 时,y最小值=k
当x= 时,y最小值=
当x=-m时,y最大值=k
当x= 时,y最大值=
y
x
o
o
y
x
1
3
3
0
x
y
11.若A(-1,y1),B(-2,y2)是抛物线y=(x-2)2-1上的两点,则y1___y2(填>,<或=)
变式1:若A(-1,y1),B(-2,y2)是抛物线y=(x-2)2+C上的两点,则y1___y2(填>,<或=)
变式2:若A(-1,y1),B(2.5,y2)是抛物线y=(x-2)2+C上的两点,则y1___y2(填>,<或=)
<
<
>
利用函数对称性:
观察点到对称轴的距离与函数值大小的关系
观察图中的抛物线,你能得到有关这个二次函数的哪些结论?(结合已学过的性质)
1
3
3
0
x
y
已知二次函数y = x2 - 4x + 3
问题1:当y=0时, x为何值?
当y=3时, x为何值?
当y=-1时,x为何值?
变式:当m为何值时,方程x2-4x+3=m,
有两个不相等的实数根;
1
3
3
0
x
y
方程问题(数)
转化
函数问题(形)
有两个相等的实数根;
无实数根;
m>-1
m=-1
m<-1
当y=-2时,x为何值?
y=0
P(2,-1)
y=3
y=-1
y=-2
4
y = x2 - 4x + 3
(2)不等式x2-4x+3>kx+b的解为_______
(3)不等式x2-4x+3
3
3
0
x
y
4
不等式问题(数)
转化
函数问题(形)
?
?
?
问题2:直线y=kx+b(k≠0)与抛物线y=x2-4x+3交于 ( ,6),
B(4,2)两点,则:
(1)方程x2-4x+3=kx+b的解为_______
?
?
P(2,-1)
问题3:如图,已知二次函数y = x2 - 4x + 3,P为顶点,B(3,0),C(0,3)
(1)求△ PBC的面积。
1
3
3
0
x
y
y=x2-4x+3
A
B
C
问题3:(2)点Q是抛物线y=x2-4x+3(1< x <3)上的一个动点。 Q的横坐标为m, 若△QBC的面积为s,求出s关于m的函数关系式。
(3)当m取何值时, S的面积最大,最大面积为多少?
1
3
3
0
x
y
y=x2-4x+3
A
B
C
Q
x
y
o
y = x2 - 4x + 3
A(1,0)
B(3,0)
C(0,3)
P(2,-1)
直线x=2
M
问题4:对称轴上是否存在点M,
使△AMC周长最小?若存在请你
求出点M的坐标;
若不存在请说明理由。
M
x
y
o
A(1,0)
B(3,0)
C(0,3)
P(2,-1)
直线x=2
G
问题4:对称轴上是否存在点M,
使△AMC周长最小?若存在请你
求出点M的坐标;
若不存在请说明理由。
y = x2 - 4x + 3
分享收获
思想方法
数形结合思想(用数表达,用形释义)
数缺形时少直观,形缺数时难入微,
两者结合万般好,隔离分家万事休 。
——华罗庚
小结
回顾与反思
?
二次函数的解析式
名称
顶点式
一般式
交点式
二次函数解析式
对称轴
顶点坐标
增减性
a>0
a<0
最值
a>0
a<0
y=a(x+m)2+k
y=ax2+bx+c
y=a(x-x1)(x-x2)
直线x=-m
直线x=
直线x=
(-m,k)
( )
当x≤-m时,y随x的增大而减小;当x≥-m时,y随x的增大而增大
当x ≤ 时,y随x的增大而减小;当x ≥ 时y随x的增大而增大
当x≤-m时,y随的增大而增大;当x≥-m时,y随的增大而减小
当x≤ 时,y随x的增大而增大;当x≥ 时y随x的增大而减小
当 x=-m 时,y最小值=k
当x= 时,y最小值=
当x=-m时,y最大值=k
当x= 时,y最大值=
y
x
o
o
y
x
1
3
3
0
x
y
11.若A(-1,y1),B(-2,y2)是抛物线y=(x-2)2-1上的两点,则y1___y2(填>,<或=)
变式1:若A(-1,y1),B(-2,y2)是抛物线y=(x-2)2+C上的两点,则y1___y2(填>,<或=)
变式2:若A(-1,y1),B(2.5,y2)是抛物线y=(x-2)2+C上的两点,则y1___y2(填>,<或=)
<
<
>
利用函数对称性:
观察点到对称轴的距离与函数值大小的关系
同课章节目录
