浙教版初中数学九年级上册 1.2 二次函数图像 课件(14张)
文档属性
| 名称 | 浙教版初中数学九年级上册 1.2 二次函数图像 课件(14张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 228.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-12 21:31:57 | ||
图片预览




文档简介
1.2 二次函数的图象(1)
回顾知识:
一、正比例函数y=kx(k ≠ 0)其图象是什么。
二、一次函数y=kx+b(k ≠ 0)其图象又是什么。
正比例函数y=kx(k ≠ 0)其图象是一条经过原点的直线。
一次函数y=kx+b(k ≠ 0)其图象也是一条直线。
三、反比例函数 (k ≠ 0)其图象又是什么。
反比例函数 (k ≠ 0)其图象是双曲线。
二次函数y=ax?+ bx+c(a ≠ 0)
其图象又是什么呢?。
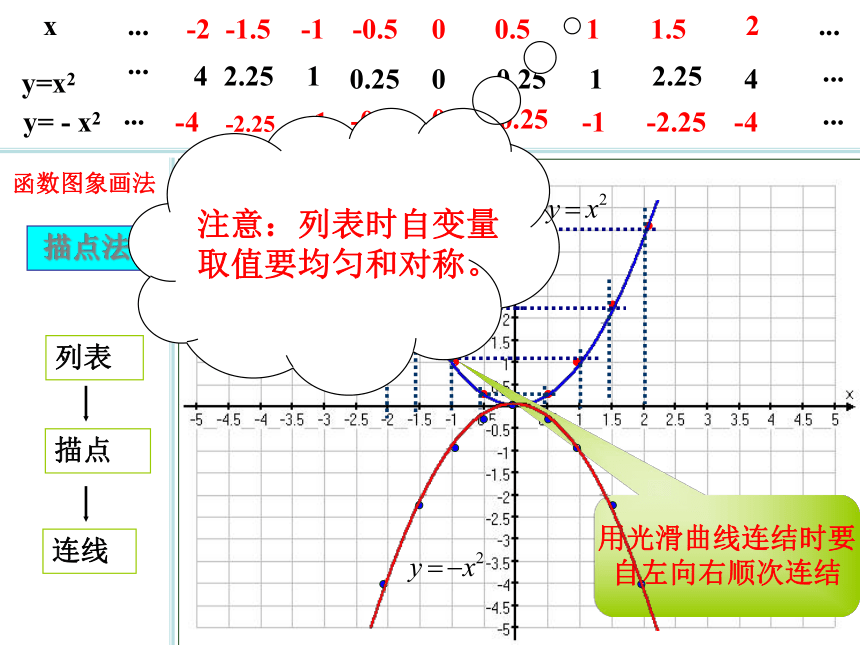
二次函数y=ax2的图像
x
y=x2
y= - x2
...
...
...
...
...
...
0
-2
-1.5
-1
-0.5
1
1.5
0.5
2
函数图象画法
列表
描点
连线
0
0.25
1
2.25
4
0.25
1
2.25
4
描点法
用光滑曲线连结时要
自左向右顺次连结
0
-0.25
-1
-2.25
-4
-0.25
-1
-2.25
-4
注意:列表时自变量
取值要均匀和对称。
x
y=x2
...
...
...
...
0
-4
-3
-2
-1
2
3
1
4
x
y=2x2
...
...
...
...
0
-2
-1.5
-1
-0.5
1
1.5
0.5
2
0
0.5
2
4.5
8
0.5
2
4.5
8
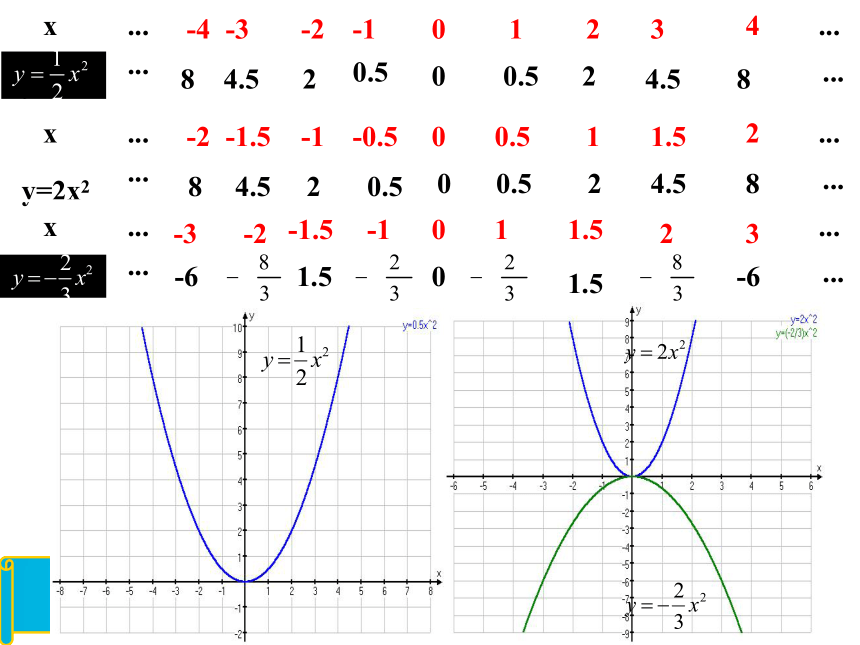
列表参考
0
0.5
2
4.5
8
0.5
2
4.5
8
x
y=2x2
...
...
...
...
0
-3
-1.5
-1
1.5
1
-2
2
3
0
1.5
-6
1.5
-6
抛物线y=ax2具有以下特征:
(1)开口方法由a的符号确定,简记“上正下负”.
(2)开口大小由|a| 的决定,
|a|越大,抛物线的开口越小;
|a|越小,抛物线的开口越大
(3)对称轴是y轴,即直线x=0
(4)顶点坐标是(0,0),当a>0时,
(0,0)是最低点;当a<0时,(0,0)是最高点.
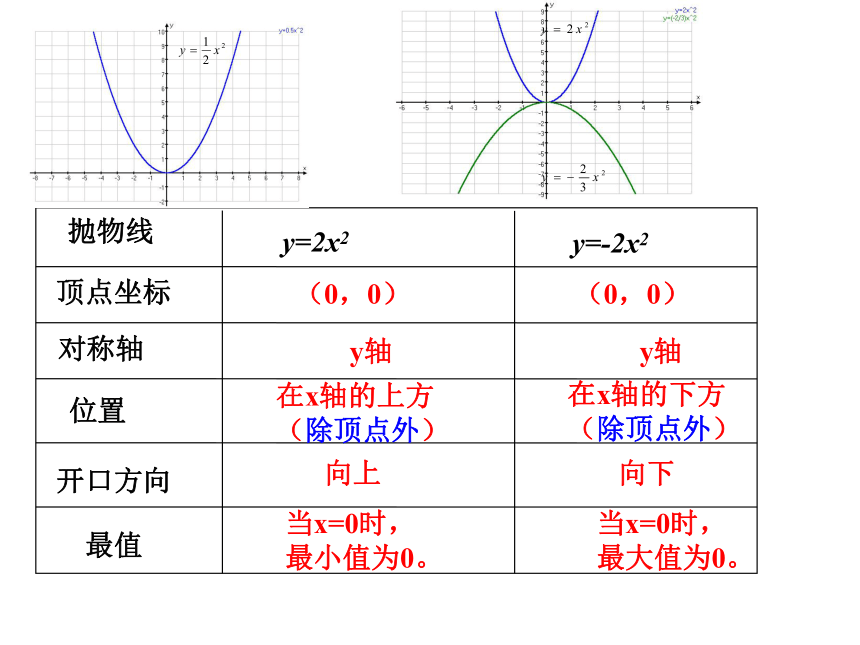
抛物线
y=2x2
y=-2x2
顶点坐标
对称轴
位置
开口方向
最值
(0,0)
(0,0)
y轴
y轴
在x轴的上方
(除顶点外)
在x轴的下方
(除顶点外)
向上
向下
当x=0时,
最小值为0。
当x=0时,
最大值为0。
(2)抛物线 的开口方向为 ,
对称轴是 ,顶点坐标是 ,顶
点是这条抛物线的最 点.
(1)抛物线 的开口方向为 ,
对称轴是 ,顶点坐标是 ,顶
点是这条抛物线的最 点;
例1、已知二次函数y=ax2(a≠0)的图像经过点(-2,-3).
(1)求a的值,并写出这个二次函数的解析式.
(2)说出这个二次函数的顶点坐标、对称轴、开口方向和图像的位置.
练习一、已知抛物线y=ax2经过点A(-2,-8)。
(1)求此抛物线的函数解析式;
(2)判断点B(-1,- 4)是否在此抛物线上。
(3)求出此抛物线上纵坐标为-6的点的坐标。
解(1)把(-2,-8)代入y=ax2,得
-8=a(-2)2,解出a= -2,
所求函数解析式为 y= -2x2.
(2)因为 ,所以点B(-1 ,-4)
不在此抛物线上。
(3)由-6=-2x2 ,得x2=3,
所以纵坐标为-6的点有两个,
它们分别是
某涵洞是抛物线形,它的截面如图所示,现测得水面
宽AB=1.6m,涵洞顶点O到水面的距离为2.4m,在图
中直角坐标系内,涵洞所在抛物线的函数表达式
如图所示,已知函数y= -2x+3与y=x2的图象交于A,B
两点,且与x轴、y轴交于D,C两点,O为坐标原点.
(1)求点A,B的坐标;
(2)求S△AOB.
课堂小结
形如 (a、b、c是常数,a≠0)的函数叫做 x 的二次函数,a叫做二次函数的系数,b叫做一次项的系数,c叫作常数项。
1. 二次函数:
2、抛物线:
二次函数的图象都是抛物线。
一般地,抛物线 y=ax2 的对称轴是____轴,顶点是_______. 当a > 0时,抛物线的开口向__,顶点是抛物线的________,a 越大,抛物线的开口越___;当a < 0时,抛物线的开口向____,顶点是抛物线的最____点,a 越大,抛物线的开口越____.
y
原点
最低点
上
小
下
高
大
3、抛物线 y=ax2 的图象 :
4、抛物线 y=ax2 的图象 中a决定开口方向和形状。
a相同开口方向相同、形状相同,|a|越大,开口越小。
回顾知识:
一、正比例函数y=kx(k ≠ 0)其图象是什么。
二、一次函数y=kx+b(k ≠ 0)其图象又是什么。
正比例函数y=kx(k ≠ 0)其图象是一条经过原点的直线。
一次函数y=kx+b(k ≠ 0)其图象也是一条直线。
三、反比例函数 (k ≠ 0)其图象又是什么。
反比例函数 (k ≠ 0)其图象是双曲线。
二次函数y=ax?+ bx+c(a ≠ 0)
其图象又是什么呢?。
二次函数y=ax2的图像
x
y=x2
y= - x2
...
...
...
...
...
...
0
-2
-1.5
-1
-0.5
1
1.5
0.5
2
函数图象画法
列表
描点
连线
0
0.25
1
2.25
4
0.25
1
2.25
4
描点法
用光滑曲线连结时要
自左向右顺次连结
0
-0.25
-1
-2.25
-4
-0.25
-1
-2.25
-4
注意:列表时自变量
取值要均匀和对称。
x
y=x2
...
...
...
...
0
-4
-3
-2
-1
2
3
1
4
x
y=2x2
...
...
...
...
0
-2
-1.5
-1
-0.5
1
1.5
0.5
2
0
0.5
2
4.5
8
0.5
2
4.5
8
列表参考
0
0.5
2
4.5
8
0.5
2
4.5
8
x
y=2x2
...
...
...
...
0
-3
-1.5
-1
1.5
1
-2
2
3
0
1.5
-6
1.5
-6
抛物线y=ax2具有以下特征:
(1)开口方法由a的符号确定,简记“上正下负”.
(2)开口大小由|a| 的决定,
|a|越大,抛物线的开口越小;
|a|越小,抛物线的开口越大
(3)对称轴是y轴,即直线x=0
(4)顶点坐标是(0,0),当a>0时,
(0,0)是最低点;当a<0时,(0,0)是最高点.
抛物线
y=2x2
y=-2x2
顶点坐标
对称轴
位置
开口方向
最值
(0,0)
(0,0)
y轴
y轴
在x轴的上方
(除顶点外)
在x轴的下方
(除顶点外)
向上
向下
当x=0时,
最小值为0。
当x=0时,
最大值为0。
(2)抛物线 的开口方向为 ,
对称轴是 ,顶点坐标是 ,顶
点是这条抛物线的最 点.
(1)抛物线 的开口方向为 ,
对称轴是 ,顶点坐标是 ,顶
点是这条抛物线的最 点;
例1、已知二次函数y=ax2(a≠0)的图像经过点(-2,-3).
(1)求a的值,并写出这个二次函数的解析式.
(2)说出这个二次函数的顶点坐标、对称轴、开口方向和图像的位置.
练习一、已知抛物线y=ax2经过点A(-2,-8)。
(1)求此抛物线的函数解析式;
(2)判断点B(-1,- 4)是否在此抛物线上。
(3)求出此抛物线上纵坐标为-6的点的坐标。
解(1)把(-2,-8)代入y=ax2,得
-8=a(-2)2,解出a= -2,
所求函数解析式为 y= -2x2.
(2)因为 ,所以点B(-1 ,-4)
不在此抛物线上。
(3)由-6=-2x2 ,得x2=3,
所以纵坐标为-6的点有两个,
它们分别是
某涵洞是抛物线形,它的截面如图所示,现测得水面
宽AB=1.6m,涵洞顶点O到水面的距离为2.4m,在图
中直角坐标系内,涵洞所在抛物线的函数表达式
如图所示,已知函数y= -2x+3与y=x2的图象交于A,B
两点,且与x轴、y轴交于D,C两点,O为坐标原点.
(1)求点A,B的坐标;
(2)求S△AOB.
课堂小结
形如 (a、b、c是常数,a≠0)的函数叫做 x 的二次函数,a叫做二次函数的系数,b叫做一次项的系数,c叫作常数项。
1. 二次函数:
2、抛物线:
二次函数的图象都是抛物线。
一般地,抛物线 y=ax2 的对称轴是____轴,顶点是_______. 当a > 0时,抛物线的开口向__,顶点是抛物线的________,a 越大,抛物线的开口越___;当a < 0时,抛物线的开口向____,顶点是抛物线的最____点,a 越大,抛物线的开口越____.
y
原点
最低点
上
小
下
高
大
3、抛物线 y=ax2 的图象 :
4、抛物线 y=ax2 的图象 中a决定开口方向和形状。
a相同开口方向相同、形状相同,|a|越大,开口越小。
同课章节目录
