浙教版数学八年级上册 5.4 一次函数的图像与性质(复习课)(共18张ppt)
文档属性
| 名称 | 浙教版数学八年级上册 5.4 一次函数的图像与性质(复习课)(共18张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-12 21:25:44 | ||
图片预览




文档简介
复习:一次函数的图象和性质
浙教版八年级上册
学习目标
1. 进一步掌握一次函数的图象和性质
2. 能够利用一次函数的性质解决实际问题
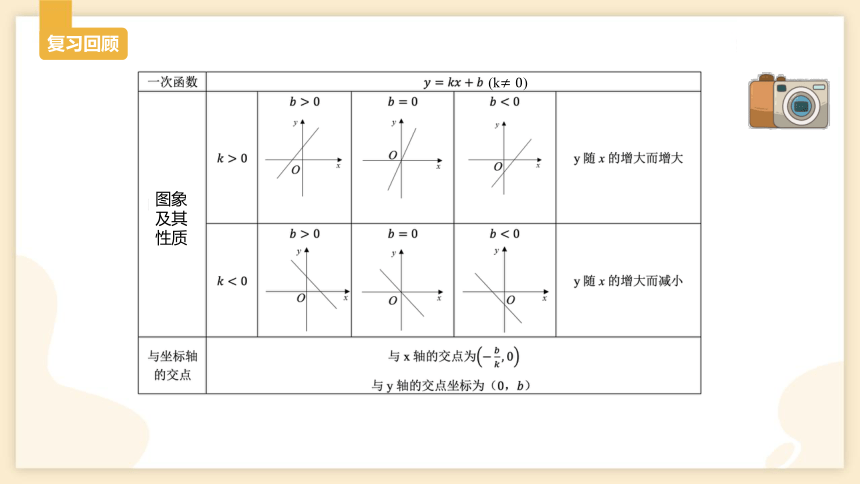
复习回顾
(k≠0)
?
图象及其性质
基础巩固
1. 已知一次函数y=kx+b的图象如图所示,则下列语句中不正确的是( )
A. 函数值y随x的增大而增大 B. 当x>0时,y>0
C. k+b=0 D. kb<0
1
O
B
基础巩固
预4:正比例函数????=????????(????≠0)的函数值????随????的增大而减小,则一次函数????=?????????+?????2的图象大致是( )
?
A
A.
B.
C.
D.
变2: 直线????=????????+????经过二、三、四象限,则直线????=?????????????的图象只能是图中的( )
?
A.
B.
C.
D.
C
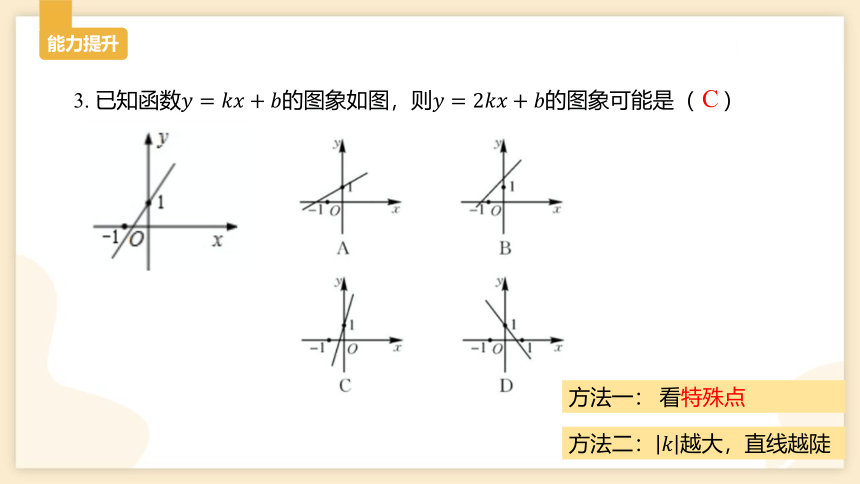
能力提升
C
方法二:????越大,直线越陡
?
3. 已知函数????=????????+????的图象如图,则????=2????????+????的图象可能是( )
?
方法一: 看特殊点
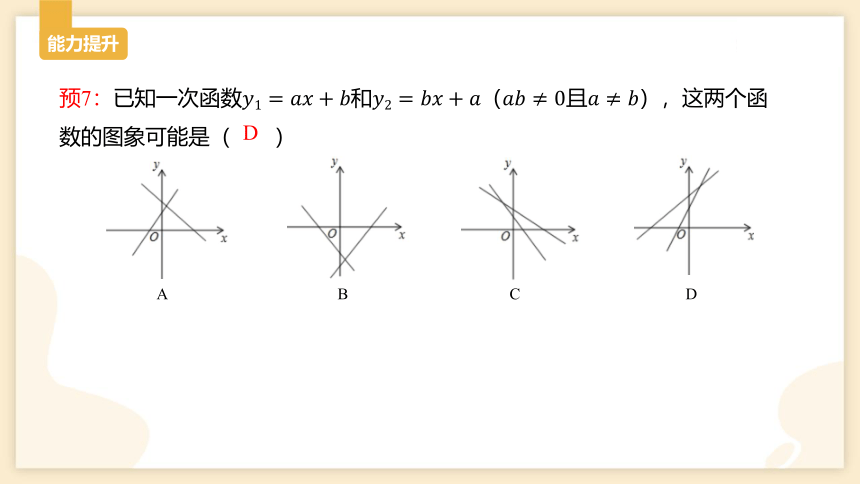
能力提升
预7:已知一次函数????1=????????+????和????2=????????+????(????????≠0且????≠????),这两个函数的图象可能是( )
?
A B C D
D
能力提升
变4:一次函数????=?????????????与????=????????????(????????≠0),在同一平面直角坐标系的图像不可能是( )
?
A B C D
C
能力提升
变5:一次函数????=????????+????与????=????????????(????????≠0),在同一平面直角坐标系的图像不可能是( )
?
A B C D
分类讨论思想
预7:已知一次函数????1=????????+????和????2=????????+????(????????≠0且????≠????),这两个函数的图象可能是( )
?
A B C D
D
C
实际应用
分析:月收入y=底薪(900元)+计件工资
计件工资=A型服装工资+B型服装工资
6. 小李是某服装厂的一名工人,负责加工A,B两种型号服装,他每月的工作时间为22天,月收入由底薪和计件工资两部分组成,其中底薪900元,加工A型服装1件可得20元,加工B型服装1件可得12元.已知小李每天可加工A型服装4件或B型服装8件,设他每月加工A型服装的时间为x天,月收入为y元.
(1)求y与x的函数关系式;
(2)根据服装厂要求,小李每月加工A型服装数量应不少于B型服装数量的 35,那么他的月收入最高能达到多少元?
?
实际应用
解:(1)????=?16????+3012
(2)依题意得,4????≥35×8×22?????,
解得???????≥12.
在????=?16????+3012中,
∵-16<0,y随x的增大而减小
∴当????=12时,y取最大值,此时????=?16×12+3012=2820.
答:当小李每月加工A型服装12天时,月收入最高,可达2820元.
?
6. 小李是某服装厂的一名工人,负责加工A,B两种型号服装,他每月的工作时间为22天,月收入由底薪和计件工资两部分组成,其中底薪900元,加工A型服装1件可得20元,加工B型服装1件可得12元.已知小李每天可加工A型服装4件或B型服装8件,设他每月加工A型服装的时间为x天,月收入为y元.
(1)求y与x的函数关系式;
(2)根据服装厂要求,小李每月加工A型服装数量应不少于B型服装数量的 35,那么他的月收入最高能达到多少元?
?
著名数学家华罗庚:
数缺形时少直观,
形少数时难入微。
数形结合百般好,
隔离分家万事休。
课堂小结
一、主要内容
三、数学思想
数形结合、分类讨论、化归思想
(k≠0)
?
二、主要方法
看图、看增减性、看特殊点
下课啦
乐课网智慧教育研究院 初中数学
浙教版八年级上册
基础巩固
2. 已知直线????=5?????3????+2?????.
(1)当m为何值时,y随x的增大而减小?
(2)当n为何值时,直线与y轴的交点在x轴的上方?
(3)当m,n为何值时,直线经过第一、二、四象限?
?
解:(1)5?????3<0,????<35时,y随x增大而减小.
(2)2?????>0,????<2时,直线与y轴交点在x轴上方.
(3)5?????3<02?????>0,????<35????<2,图象在一、二、四象限.
?
实际应用
某手机店销售一部A型手机比销售一部B型手机获得的利润多50元,销售相同数量的A型手机和B型手机获得的利润分别为3000元和2000元.
(1)求每部A型手机和B型手机的销售利润分别为多少元?
(2)该商店计划一次购进两种型号的手机共110部,其中A型手机的进货量不超过B型手机的2倍,设购进B型手机n部,这110部手机的销售总利润为y元.
①求y关于n的函数关系式;
②该手机店购进A型、B型手机各多少部,才能使销售总利润最大?
解:(1)每部A型手机的销售利润为150元,每部B型手机的销售利润为100元.
(2)①????=-50????+16?500(????≥3623,????为整数).
②∵-50<0,
∴y随n的增大而减小.
∵????≥3623,????为整数,
∴当????=37时,y取得最大值,最大值为-50×37+16500=14650(元),
答:购进A型手机73部、B型手机37部时,才能使销售总利润最大.
?
实际应用
某手机店销售一部A型手机比销售一部B型手机获得的利润多50元,销售相同数量的A型手机和B型手机获得的利润分别为3000元和2000元.
(1)求每部A型手机和B型手机的销售利润分别为多少元?
(2)该商店计划一次购进两种型号的手机共110部,其中A型手机的进货量不超过B型手机的2倍,设购进B型手机n部,这110部手机的销售总利润为y元.
①求y关于n的函数关系式;
②该手机店购进A型、B型手机各多少部,才能使销售总利润最大?
(3)实际进货时,厂家对B型手机出厂价下调m(30(3)根据题意,得????=(????-50)????+16500,其中,36≤????≤80.
①当30②当????=50时,????-50=0,????=16500,即商店购进B型手机数量满足36≤????≤80的整数时,均获得最大利润.
③当50?
变式题3:若点????(?3,????1)和点????(2,????2)都在????=(?????2?1)????+3 的图像上,那么y1与y2的大小关系是( )
A. ????1≤????2????????????????????????B. ????1=????2???????????????????C. ????1????2
?
D
浙教版八年级上册
学习目标
1. 进一步掌握一次函数的图象和性质
2. 能够利用一次函数的性质解决实际问题
复习回顾
(k≠0)
?
图象及其性质
基础巩固
1. 已知一次函数y=kx+b的图象如图所示,则下列语句中不正确的是( )
A. 函数值y随x的增大而增大 B. 当x>0时,y>0
C. k+b=0 D. kb<0
1
O
B
基础巩固
预4:正比例函数????=????????(????≠0)的函数值????随????的增大而减小,则一次函数????=?????????+?????2的图象大致是( )
?
A
A.
B.
C.
D.
变2: 直线????=????????+????经过二、三、四象限,则直线????=?????????????的图象只能是图中的( )
?
A.
B.
C.
D.
C
能力提升
C
方法二:????越大,直线越陡
?
3. 已知函数????=????????+????的图象如图,则????=2????????+????的图象可能是( )
?
方法一: 看特殊点
能力提升
预7:已知一次函数????1=????????+????和????2=????????+????(????????≠0且????≠????),这两个函数的图象可能是( )
?
A B C D
D
能力提升
变4:一次函数????=?????????????与????=????????????(????????≠0),在同一平面直角坐标系的图像不可能是( )
?
A B C D
C
能力提升
变5:一次函数????=????????+????与????=????????????(????????≠0),在同一平面直角坐标系的图像不可能是( )
?
A B C D
分类讨论思想
预7:已知一次函数????1=????????+????和????2=????????+????(????????≠0且????≠????),这两个函数的图象可能是( )
?
A B C D
D
C
实际应用
分析:月收入y=底薪(900元)+计件工资
计件工资=A型服装工资+B型服装工资
6. 小李是某服装厂的一名工人,负责加工A,B两种型号服装,他每月的工作时间为22天,月收入由底薪和计件工资两部分组成,其中底薪900元,加工A型服装1件可得20元,加工B型服装1件可得12元.已知小李每天可加工A型服装4件或B型服装8件,设他每月加工A型服装的时间为x天,月收入为y元.
(1)求y与x的函数关系式;
(2)根据服装厂要求,小李每月加工A型服装数量应不少于B型服装数量的 35,那么他的月收入最高能达到多少元?
?
实际应用
解:(1)????=?16????+3012
(2)依题意得,4????≥35×8×22?????,
解得???????≥12.
在????=?16????+3012中,
∵-16<0,y随x的增大而减小
∴当????=12时,y取最大值,此时????=?16×12+3012=2820.
答:当小李每月加工A型服装12天时,月收入最高,可达2820元.
?
6. 小李是某服装厂的一名工人,负责加工A,B两种型号服装,他每月的工作时间为22天,月收入由底薪和计件工资两部分组成,其中底薪900元,加工A型服装1件可得20元,加工B型服装1件可得12元.已知小李每天可加工A型服装4件或B型服装8件,设他每月加工A型服装的时间为x天,月收入为y元.
(1)求y与x的函数关系式;
(2)根据服装厂要求,小李每月加工A型服装数量应不少于B型服装数量的 35,那么他的月收入最高能达到多少元?
?
著名数学家华罗庚:
数缺形时少直观,
形少数时难入微。
数形结合百般好,
隔离分家万事休。
课堂小结
一、主要内容
三、数学思想
数形结合、分类讨论、化归思想
(k≠0)
?
二、主要方法
看图、看增减性、看特殊点
下课啦
乐课网智慧教育研究院 初中数学
浙教版八年级上册
基础巩固
2. 已知直线????=5?????3????+2?????.
(1)当m为何值时,y随x的增大而减小?
(2)当n为何值时,直线与y轴的交点在x轴的上方?
(3)当m,n为何值时,直线经过第一、二、四象限?
?
解:(1)5?????3<0,????<35时,y随x增大而减小.
(2)2?????>0,????<2时,直线与y轴交点在x轴上方.
(3)5?????3<02?????>0,????<35????<2,图象在一、二、四象限.
?
实际应用
某手机店销售一部A型手机比销售一部B型手机获得的利润多50元,销售相同数量的A型手机和B型手机获得的利润分别为3000元和2000元.
(1)求每部A型手机和B型手机的销售利润分别为多少元?
(2)该商店计划一次购进两种型号的手机共110部,其中A型手机的进货量不超过B型手机的2倍,设购进B型手机n部,这110部手机的销售总利润为y元.
①求y关于n的函数关系式;
②该手机店购进A型、B型手机各多少部,才能使销售总利润最大?
解:(1)每部A型手机的销售利润为150元,每部B型手机的销售利润为100元.
(2)①????=-50????+16?500(????≥3623,????为整数).
②∵-50<0,
∴y随n的增大而减小.
∵????≥3623,????为整数,
∴当????=37时,y取得最大值,最大值为-50×37+16500=14650(元),
答:购进A型手机73部、B型手机37部时,才能使销售总利润最大.
?
实际应用
某手机店销售一部A型手机比销售一部B型手机获得的利润多50元,销售相同数量的A型手机和B型手机获得的利润分别为3000元和2000元.
(1)求每部A型手机和B型手机的销售利润分别为多少元?
(2)该商店计划一次购进两种型号的手机共110部,其中A型手机的进货量不超过B型手机的2倍,设购进B型手机n部,这110部手机的销售总利润为y元.
①求y关于n的函数关系式;
②该手机店购进A型、B型手机各多少部,才能使销售总利润最大?
(3)实际进货时,厂家对B型手机出厂价下调m(30
①当30②当????=50时,????-50=0,????=16500,即商店购进B型手机数量满足36≤????≤80的整数时,均获得最大利润.
③当50?
变式题3:若点????(?3,????1)和点????(2,????2)都在????=(?????2?1)????+3 的图像上,那么y1与y2的大小关系是( )
A. ????1≤????2????????????????????????B. ????1=????2???????????????????C. ????1????2
?
D
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
