7.5一次函数的简单应用

(共20张PPT)
浙教版八上数学第七章一次函数
7.5一次函数的简单应用
复习巩固：
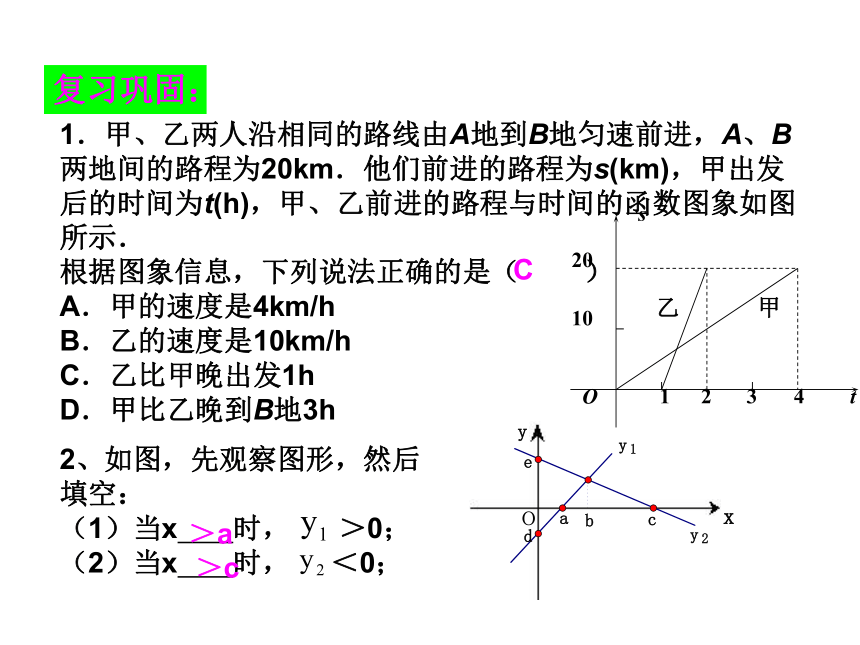
1．甲、乙两人沿相同的路线由A地到B地匀速前进，A、B两地间的路程为20km．他们前进的路程为s(km)，甲出发后的时间为t(h)，甲、乙前进的路程与时间的函数图象如图所示．
根据图象信息，下列说法正确的是（ ）
A．甲的速度是4km/h
B．乙的速度是10km/h
C．乙比甲晚出发1h
D．甲比乙晚到B地3h
O
t
s
甲
乙
1
2
3
4
20
10
C
2、如图，先观察图形，然后填空：
（1）当x 时， ＞0；
（2）当x 时， ＜0；
＞a
＞c
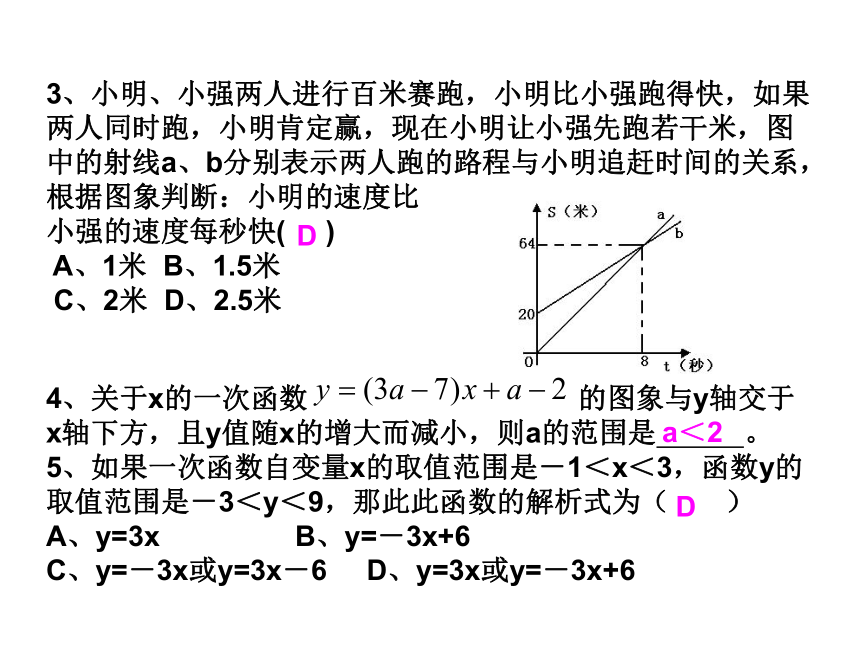
3、小明、小强两人进行百米赛跑，小明比小强跑得快，如果两人同时跑，小明肯定赢，现在小明让小强先跑若干米，图中的射线a、b分别表示两人跑的路程与小明追赶时间的关系，根据图象判断：小明的速度比
小强的速度每秒快( )
A、1米 B、1.5米
C、2米 D、2.5米
4、关于x的一次函数 的图象与y轴交于x轴下方，且y值随x的增大而减小，则a的范围是 。
5、如果一次函数自变量x的取值范围是－1＜x＜3，函数y的取值范围是－3＜y＜9，那此此函数的解析式为（ ）
A、y=3x B、y=－3x+6
C、y=－3x或y=3x－6 D、y=3x或y=－3x+6
D
a＜2
D
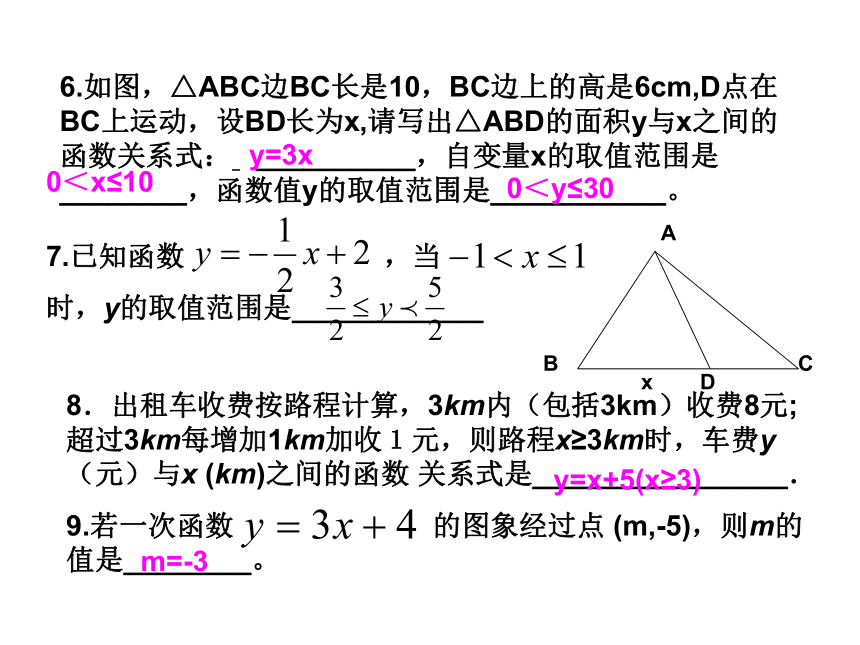
6.如图，△ABC边BC长是10，BC边上的高是6cm,D点在BC上运动，设BD长为x,请写出△ABD的面积y与x之间的函数关系式： __________，自变量x的取值范围是________，函数值y的取值范围是___________。
A
B
C
D
x
7.已知函数 ，当
时，y的取值范围是____________
8．出租车收费按路程计算，3km内（包括3km）收费8元;超过3km每增加1km加收１元，则路程x≥3km时，车费y（元）与x (km)之间的函数 关系式是________________．
9.若一次函数 的图象经过点 (m,-5)，则m的值是________。
y=3x
0＜x≤10
0＜y≤30
y=x+5(x≥3)
m=-3
总结归纳:
运用一次函数
模型解决实际
问题的基本步
骤是：
根据图象判断函数的类型
用待定系数法求出函数解析式
解决有关函数的实际问题
在实际问题解决时特别注意自变量及函数值的存在条件
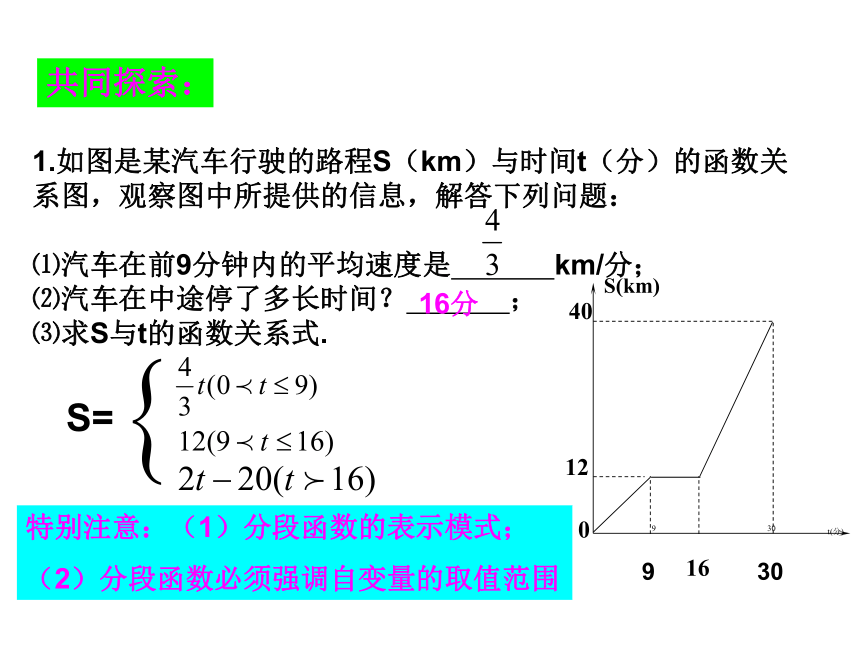
1.如图是某汽车行驶的路程S（km）与时间t（分）的函数关系图，观察图中所提供的信息，解答下列问题：
⑴汽车在前9分钟内的平均速度是 km/分；
⑵汽车在中途停了多长时间？ ；
⑶求S与t的函数关系式.
0
S(km)
t(分)
9
30
40
12
16
30
9
共同探索：
16分
S=
特别注意：（1）分段函数的表示模式；
（2）分段函数必须强调自变量的取值范围
2.为发展旅游经济．我市某景区对门票采用灵活的售票方法吸引游客．门票定价为50元/人．非节假日打a折售票．节假日按团队人数分段定价售票，即m人以下(含m人)的团队接原价售票；超过m人的团队．其中m人仍按原价售票．超过m人部分的游客打b折售票．设某旅游团人数为x人．非节假日购票款
为 (元)，节假日购票款为 (元)． 与x之间的函数图象如图8所示．
（1）观察图象可知：a=______；b=______；m=______；
（2）直接写出 与x之间的函数关系式：
（3）某旅行杜导游王娜于5月1日带A团．5月20日(非节假日)带B团都到该景区旅游．共付门票款
1900元．A，B两个团队合计50人，
求A，B两个团队各有多少人
0.6
0.9
10
(3)设A团有x人,则B团有(50-x)人。
由题意可得：40x+100+30(50-x)=1900
解得：x=30
答A团有30人，B团有20人。
3.阅读下面的材料：
在平面几何中，我们学过两条直线平行的定义.下面就两个一次函数的图象所确定的两条直线，给出它们平行的定义：设一次函数 的图象为直线 ，一次
函数 的图象为直线 ，若 ，且
我们就称直线与直线互相平行. 解答下面的问题：
（1）求过点p(1,4)且与已知直线y=2x-1平行的直线L的函数表达式,并画出直线L的图象；
（2）设直线L分别与y轴、x轴交于点A、B，如果直线m：
与直线L平行且交x轴于点C，
求出△ABC的面积s关于t的函数表达式.
2
4
6
2
4
6
－2
－2
2
4
6
2
4
6
－2
－2
(1)过点p(1,4)且与已知直线y=2x-1平行的直线L的函数表达式:y=2x+2
y=2x+2
A
B
C
C
问题（2）在考虑时特别注意存在的可能情况。
4.一农民带上若干千克自产的土豆进城出售, 为了方便, 他带了一些零钱备用,按市场价售出一些后, 又降价出售, 售出的土豆千克数x与他手中持有的钱数(含备用零钱)y的关系, 如图所示, 结合图象回答下列问题：
(1)农民自带的零钱是多少
(2)试求降价前y与x之间的关系式.
(3)由表达式你能求出降价前每
千克的土豆价格是多少
(4)降价后他按每千克0.4元将
剩余土豆售完, 这时他手中的钱
(含备用零钱)是26元, 试问
他一共带了多少千克土豆
(1)农民自带的零钱是5元；
（2）设降价前的函数解析式为：y=kx+b,经过（30，20）
（0，5）代入解方程组得：
y=0.5x+5(0＜x≤30)
(3)降价前每千克的土豆价格是0.5元。
（4）∵0.4(a-30)=6, ∴a=45。答：他一共带了45千克土豆
我们应当很好地掌握好充分利用图象信息，正确把握好函数类型，从而达到正确解决函数问题的目的。
5、如图，矩形OABC中，O为直角坐标系的原点，A、C两点的坐标分别为（3，0）、（0，5）。
（1）直接写出B点坐标；
（2）若过点C的直线CD交AB边于点D，且把矩形OABC的周长分为1∶3两部分，求直线CD的解析式；
x
O
C
A
B
y
(1).B(3,5)
D
(2)设D（3，y)
∴3(3+5-y)=8+y ∴y=4 ∴D(3,4)
设直线CD的解析式为：y=kx+b把C（0，5）D（3，4）代入解方程组得：
1、若直线y=2x+b与两坐标轴围成的三角形的面积是9，则b= .
2、如果一次函数y=mx+1与y=nx－2的图象相交于x轴上一点，那么m∶n= .
3、已知直线m与直线y=－0.5x+2平行，且与y轴交点的纵坐标为8，求直线m的解析式.
能力提升：
4、已知一次函数y=kx+b的图象过点（1，2），且与y轴交于点P，若直线y=－0.5x+2与y轴的交点为Q，点Q与点p关于x轴对称，求这个函数解析式.
±6
-1:2
解设直线m的解析式为y=kx+b,∵m∥y=-0.5x+2, ∴k=-0.5
∵与y轴交点的纵坐标为8, ∴b=8, ∴y=-0.5x+8
y=4x-2
5.通过市场调查，一段时间内某地区特种农产品的需求量y（千克）与市场价格x（元/千克）存在下列函数关系式：
y= (0产品的生产数量z（千克）与市场价格x（元/千克）成正比例关系：z=400x(0(1)根据以上市场调查，请你分析当市场处于平衡状态时，该地区这种农产品的市场价格与这段时间内农民的总销售收入各是多少？
6.4×100米拉力赛是学校运动会最精彩的项目之一。图中的实线和虚线分别是初三（1）班和初三（2）班代表队在比赛时运动员所跑的路程y(米)与所用时间x(秒)的函数图象(假设每名运动员跑步速度不变，交接棒时间忽略不计)。
问题：
⑴初三（2）班跑得最快的是第______接力棒的运动员；
⑵发令后经过多长时间两班运动员第一次并列？
第一
三（1）班第三棒运动员：
三（2）班第三棒运动员：
37秒时。
7．已知雅美服装厂现有A种布料70米，B种布料52米，现计划用这两种布料生产M、N两种型号的时装共80套．已知做一套M型号的时装需用A种布料1.1米，B种布料0.4米，可获利50元；做一套N型号的时装需用A种布料0.6米，B种布料0.9米，可获利45元．设生产M型号的时装套数为x，用这批布料生产两种型号的时装所获得的总利润为y元．
①求y（元）与x（套）的函数关系式，并求出自变量的取值范围；②当M型号的时装为多少套时，能使该厂所获利润最大？最大利润是多？
解(1)设生产M型号x套，则N型号(80-x)套,y=5x+3600
1.1x+0.6(80-x) ≤70
0.4x+0.9(80-x) ≤52
解得：40≤x≤44
8．甲、乙两名运动员进行长跑训练，两人距终点的路程y（米）与跑步时间x（分）之间的函数图象如图所示，根据图象所提供的信息解答问题：
(1) 他们在进行 ___ 米的长跑训练，
在0＜x＜15的时 段内，速度较快的人是 ____ ；
(2) 求甲距终点的路程y（米）和跑步时间 x（分）之间的函数关系式；
(3) 当x=15时，两人相距多少米？
在15＜x＜20的时段内，求两人速度之差．
5000
甲
(2)y=-250x+5000
(3)x=15时两人相距：2000-1250=750；在15＜x＜20两人速度差：400-250=150
4．我市某乡A,B两村盛产柑桔，A村有柑桔200吨，B村有柑桔300吨．现将这些柑桔运到C,D两个冷藏仓库，已知C仓库可储存240吨，D仓库可储存260吨；从A村运往C,D两处的费用分别为每吨20元和25元，从B村运往C,D两处的费用分别为每吨15元和18元．设从A村运往仓库C的柑桔重量为x吨，A,B两村运往两仓库的柑桔运输费用分别为 元和元．（1）请填写下表，并求出 与 之间的函数关系式；
收
地
运
地
C D 总计
A 吨 200吨
B 300吨
总计 240吨 260吨 500吨
（2）试讨论两村中，哪个村的运费较少；
（3）考虑到村的经济承受能力，村的柑桔运费不得超过4830元．在这种情况下，请问怎样调运，才能使两村运费之和最小？求出这个最小值．
一次函数
应用：
总结：
分析处理文字信息和图象信息
分析出函数类型设出一般式
求出函数达到问题的解决
分段函数解决时特别注意自变量取值范围
实际问题
数据获得
画出图象
确定函数类型
求解验证结果