浙教版九上数学相似三角形复习

(共19张PPT)
相似三角形复习
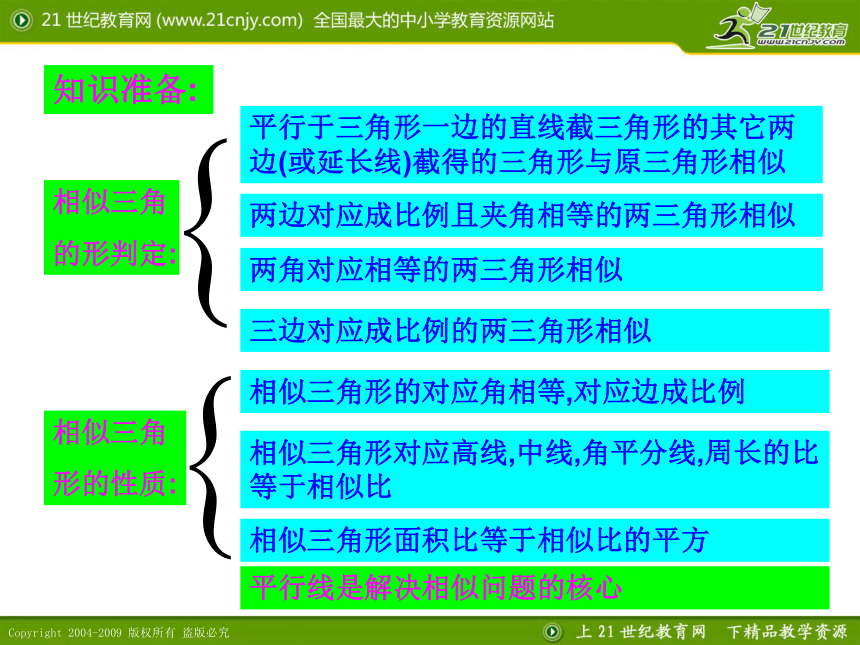
知识准备:
相似三角
的形判定:
平行于三角形一边的直线截三角形的其它两边(或延长线)截得的三角形与原三角形相似
两边对应成比例且夹角相等的两三角形相似
两角对应相等的两三角形相似
三边对应成比例的两三角形相似
相似三角
形的性质:
相似三角形的对应角相等,对应边成比例
相似三角形对应高线,中线,角平分线,周长的比等于相似比
相似三角形面积比等于相似比的平方
平行线是解决相似问题的核心
知识链接:
1、已知3x=4y，则 = （ ）
A、 B、 C、 D、-
2、若x是3和6的比例中项，则x的值为（ ）
A、 B、 C、 D、
3、若P是线段AB的黄金分割点（PA＞PB），设AB=1，则PA的长约为 ( )
A、0.191 B、0.382 C、0.5 D、0.618
4、已知如图DE∥BC， 求 （ ）
A、 B、 C、2 D、3
A
D
D
B
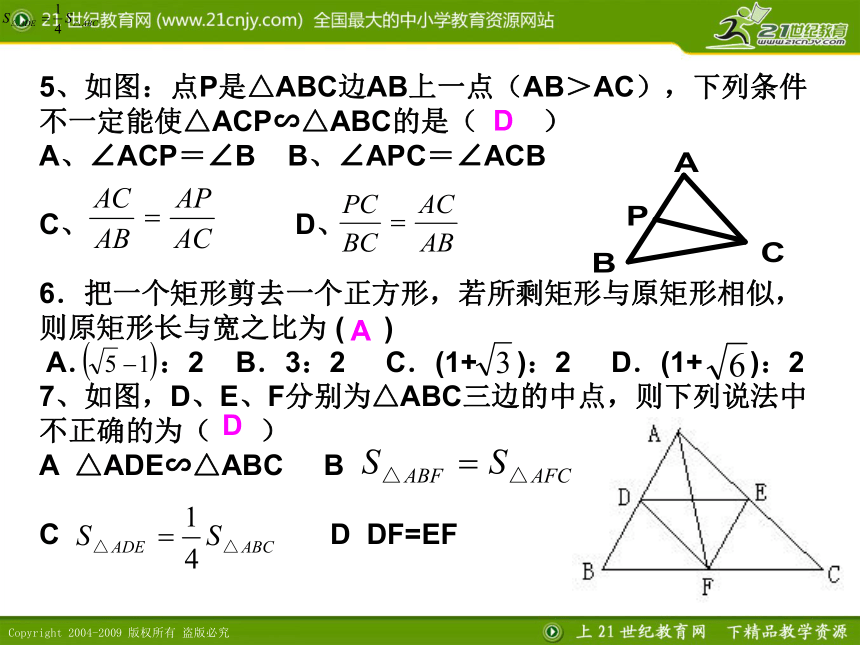
5、如图：点P是△ABC边AB上一点（AB＞AC），下列条件不一定能使△ACP∽△ABC的是（ ）
A、∠ACP＝∠B B、∠APC＝∠ACB
C、 D、
6．把一个矩形剪去一个正方形，若所剩矩形与原矩形相似，则原矩形长与宽之比为 ( )
A． ：2 B．3：2 C．(1+ )：2 D．(1+ )：2
7、如图，D、E、F分别为△ABC三边的中点，则下列说法中不正确的为（ ）
A △ADE∽△ABC B
C D DF=EF
D
A
D
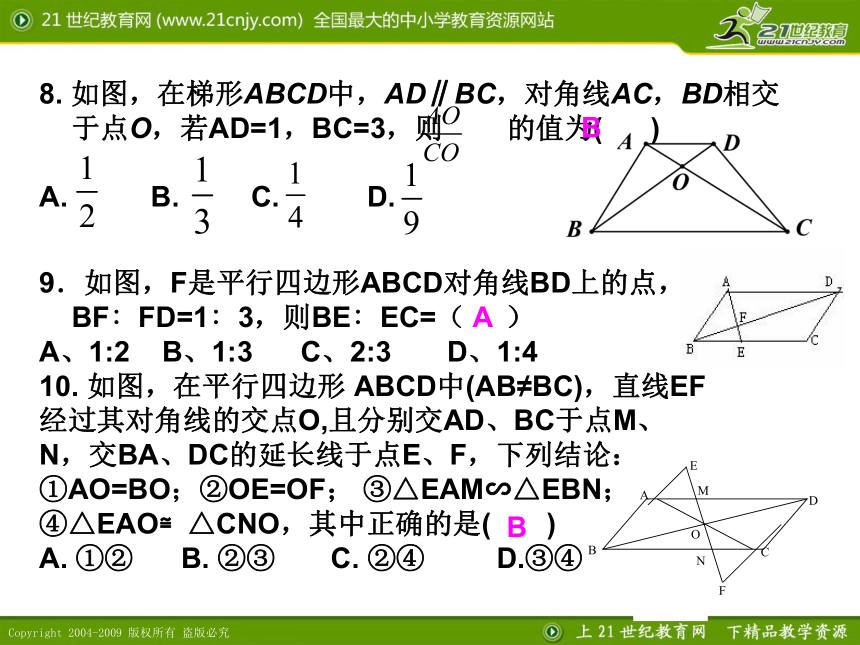
8. 如图，在梯形ABCD中，AD∥BC，对角线AC，BD相交于点O，若AD=1，BC=3，则 的值为( )
B. C. D.
9．如图，F是平行四边形ABCD对角线BD上的点，BF∶FD=1∶3，则BE∶EC=（ ）
A、1:2 B、1:3 C、2:3 D、1:4
10. 如图，在平行四边形 ABCD中(AB≠BC)，直线EF
经过其对角线的交点O,且分别交AD、BC于点M、
N，交BA、DC的延长线于点E、F，下列结论：
①AO=BO；②OE=OF； ③△EAM∽△EBN；
④△EAO≌△CNO，其中正确的是( )
A. ①② B. ②③ C. ②④ D.③④
B
A
B
A
B
C
D
E
P
Q
H
11.D,H分别是AB和BC的中点,E是AC的五等分点,求:AP:PQ:QH.
A
B
C
E
F
D
12.已知E,F分别是三等分点,D是AC的中点,求BP:PQ:QD.
P
Q
K
解:过E作EK∥BC,
M
过D作DM∥BC,
H
作DH∥BC,
相似问题中几个重要且常用的知识点:
A
B
C
共同探索:
1.已知:如图,CE是RtΔABC的斜边AB上
的高,BG⊥AP. 求证:
∴△AEC～△CEB，∴CE2=AE×EB
∵PE⊥AB，BG⊥AP，∴∠BED=∠PGD=900，∠PDG=∠BDE
∴∠DBE=∠APE，又∵∠PEA=∠BED
∴△PEA～△BED，
这一类问题关键是找到两对相似三角形的连接点
2.点P是正方形ABCD边AB上一点(不与点A．B重合)，连接PD并将线段PD绕点P顺时针方向旋转90°得到线段PE， PE交边BC于点F．连接BE、DF。
（1）求证：∠ADP=∠EPB；
（2）求∠CBE的度数；
（3）当 时．△PFD∽△BFP？并说明理由．
H
（2）过E作AB延长线的垂线，垂足为H，于上得到△ADP≌△HPE，得到BH=EH∴∠CBE=450
∵∠DPF=∠PBF，∴ △PFD∽△BFP
在许多特殊图形中，我们也常用计算法来解决三角形的相似问题。
3.如图，在 的外接圆O中，D是 的中点，AD交BC于点E，连结BD．
（1）列出图中所有相似三角形；
（2）连结DC，若在 上任取一点K（点A,B,C除外），连结CK,DK,DK交BC于点F， 是否成立？若成立，给出证明；若不成立，举例说明．
解(1)
K
F
△CFD～△KCD
4.如图，在矩形ABCD中，AB＝6米，BC＝8米，动点P以2米/秒的速度从点A出发，沿AC向点C移动，同时动点Q以1米/秒的速度从点C出发，沿CB向点B移动，设P、Q两点移动t秒（0（1）求面积S与时间t的关系式；
（2）在P、Q两点移动的过程中，四边形ABQP与△CPQ的面积能否相等？若能，求出此时点P的位置；若不能，请说明理由。
H
5.如图，抛物线 与x轴相交于点A、B，与y轴相交于点C．
（1）求证：△AOC∽△COB；
（2）过点C作CD∥x轴交抛物线于点D．若点P在线段AB上以每秒1个单位的速度由A向B运动，同时点Q在线段CD上也以每秒1个单位的速度由D向C运动，则经过几秒后，
PQ＝AC．
x
y
A
C
B
O
D
P
Q
∴ △AOC∽△COB
H
K
（2）设运动时间为t,作AH⊥CD，PK⊥CD，∴5-t-t-1=1
∴t=1.5(s) 或5-t=t, ∴t=2.5(s)时，PQ=AC。
能力提升:
1.如图，△ＡＢＣ中，ＤＥ∥ＢＣ，Ｄ，Ｅ分别交边ＡＢ、AC
于Ｄ、Ｅ两点，若ＡＤ：ＡＢ＝１：３，
则△ＡＤＥ与△ＡＢＣ的面积比为_____
2.已知：x∶y∶z=2∶3∶4，则
的值为________
3、两个相似三角形的面积之比为1∶9,小三角形的周长为4,则另一个三角形的周长为_____
4.△ABC中，M在AB上，N在AC上,且MB＝4,AB＝12,
AC＝16.若△AMN与△ABC相似，则AN的长是________.
5.已知 = = 则 =_______. 　　　　　　　
1：9
12
6.如图, △ABC内接于⊙O, AD⊥BC于D, AE是⊙O的直径. 若AB=6, AC=8, AE=10, 求AD的长.
解：连接EC，∵AE是⊙O的直径，∴
∠ACE=900，∵AD⊥BC，∴∠ADB=900
∠ACE=∠ADB，又∵∠B=∠E，∴
△ADB～△ACE，
在圆中解决相似三角形类问题时，我们会充分利用同弧上的圆周角相等，直径所对圆周角是直角，圆内接四边形的外角等于内对角，这些角来解决相似三角形。
7.如图，在⊙O中，直径AB垂直于弦CD,垂足为点E，点F在
弧AC上，从A 点向C点运动(点A、C除外)，AF与DC的延长
线相交于点M。(1) 求证：△AFD∽△CFM ；
(2) 点F在运动中是否存在一个位置使△FMD为等腰三角形,
若存在,给予证明；若不存在,请说明理由 .
B
D
C
E
O
F
M
A
B
C
D
（1）证明：∵AB是⊙O的直径，且AB⊥CD，
∴弧AC=弧AD，∴∠ADC=∠AFD，
∵四边形ADCF是⊙O内接四边形，∴∠MCF=∠FAD，∠MFC=∠ADC，∴∠MFC=∠AFD，∴ △AFD∽△CFM
（2）存在，∵△MFD为等腰三角形时，∠M=∠FDM，∵
∠ADF=∠M，∴∠ADF=∠MDF，∴F为∠ADM的平分线与⊙O的交点。
8.如图, 已知抛物线 与x轴的相交于A, B两点, 与y轴交于C(0, 5)点, O为原点.
(1)求抛物线的解析式和A, B两点的坐标；
(2)点P, Q分别从A, O两点同时以1cm/秒的速度沿AB, OC向B, C方向移动，用t(秒)表示移动时间. 连结PQ交BC于M点, 问是否存在t值, 使以O, P, Q为顶点的三角形与△OBC相似, 若存在, 求所有的t值；若不存在, 请说明理由.
9.如图，在Rt△ABC中，∠A=90°，AB=8，AC=6．若动点D从点B出发，沿线段BA运动到点A为止，运动速度为每秒2个单位长度．过点D作DE∥BC交AC于点E，设动点D运动的时间为x秒，AE的长为y．
(1) 求出y关于x的函数关系式，并写出自变量x的取值范围；
(2) 当x为何值时，△BDE的面积S有最大值，
最大值为多少？
A
B
C
D
E
解（1）∵DE∥BC
相信自己就等于成功！