二次函数复习——数形结合

(共11张PPT)
两者结合万般好，隔离分家万事休。
数缺形时少直观，形缺数时难入微，
——华罗庚
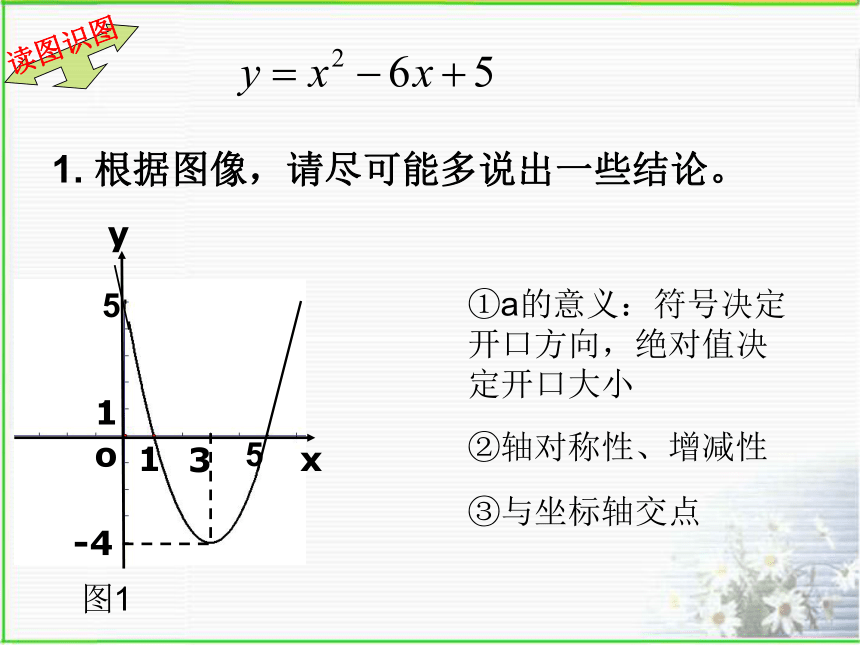
1. 根据图像，请尽可能多说出一些结论。
读图识图
1
o
3
-4
1
x
y
5
图1
①a的意义：符号决定开口方向，绝对值决定开口大小
②轴对称性、增减性
③与坐标轴交点
5
读图识图
x
y
o
4
-1
图2
1
-3
2、如图2是抛物线 的部分图像，你能求出它的解析式吗？
若把抛物线先向右平移2个单位，再向下平移3个单位，则此时抛物线对应的函数解析式为__________。
左“+”右“－”
读图识图
x
y
o
4
-1
图2
1
-3
直线y=m
3、结合图2回答：(1)当x取何值时，y=0？
y＞0
(2) 进一步，当m为何值时，方程
①有两个不相等的实数根；②有两个相等的实数根；
③无实数根？
m<4
m=4
m>4
方程问题（数）
函数问题（形）
转化
反过来，当y=0时，x取何值？
当y=1时呢？
y＜0
A
B
x
y
o
4
-1
图3
1
不等式问题（数）
函数问题（形）
转化
读图识图
【例】在火箭主场与湖人的一场比赛中，科比在距篮4米处跳投，球运行的路线是抛物线，当球运行的水平距离为2.5米时，达到最大高度3.75米，然后球准确落入篮圈，已知篮圈中心到地面的距离为3.05米.
4米
3.05米
2.5米
0
x
y
(0,3.75)
（1）建立如图所示的坐标系，求抛物线的解析式；
解：顶点（0，3.75），故可设抛物线解析式为：
把点（1.5，3.05）代入得：
解得：
抛物线解析式为：
(1.5,3.05)
（2）姚明身高为2.26米，跳起能摸到高度为3.45米，此时他上前封盖，在离科比2米处时起跳,问能否成功封盖住科比的此次投篮
解：-2.5+2=-0.5
当
时，
姚明此次不能成功封盖科比的这次投篮.
4米
2.5米
3.05米
0
x
y
(0,3.75)
-0.98
-0.5
3.67
3.45
（3）若姚明能成功封盖科比的这次投篮，他离科比的距离在什么范围内呢？（精确到厘米）
解：令
，得：
又
故姚明此次不能成功封盖科比的这次投篮
解，得
1、这节课你学会了……
知道了……
2、你最大的收获是……
如图，在直角梯形ABCD中,∠A=∠D=90°，
截取AE=BF=DG=x，已知AB=6，CD=3，AD=4，求：
（1）四边形DGEF的面积S关于x的函数关系式和x的取值范围；
（2）当x为何值时，
S的数值等于x的4倍？
（3）面积S是否存在最小值？
若存在，求出最小值；
若不存在，请说明理由；
A
B
C
D
E
F
G