1.3 解直角三角形(3)
图片预览


文档简介
(共15张PPT)
2.两种情况:
解直角三角形,只有下面两种情况:
(1)已知两条边;
(2)已知一条边和一个锐角
1.解直角三角形.
在直角三角形中,由已知元素求出未知元素的过程,叫做解直角三角形.
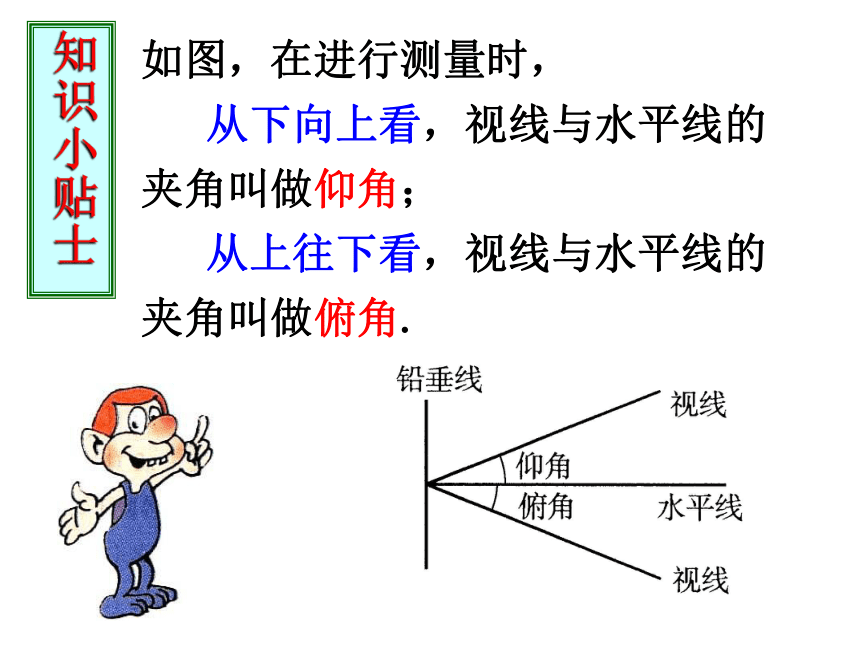
如图,在进行测量时,
从下向上看,视线与水平线的夹角叫做仰角;
从上往下看,视线与水平线的夹角叫做俯角.
知识小贴士
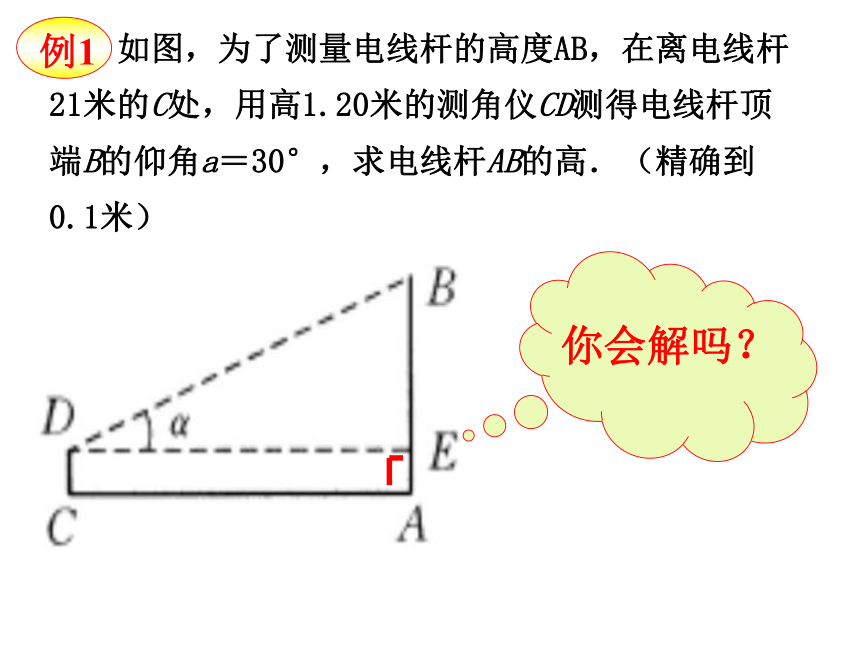
例1
如图,为了测量电线杆的高度AB,在离电线杆21米的C处,用高1.20米的测角仪CD测得电线杆顶端B的仰角a=30°,求电线杆AB的高.(精确到0.1米)
你会解吗?
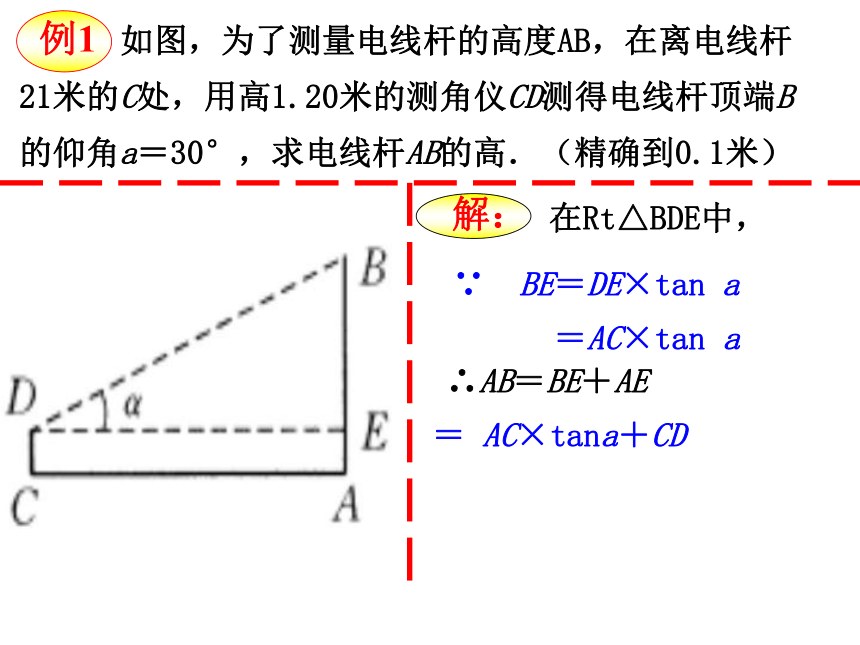
例1
在Rt△BDE中,
解:
如图,为了测量电线杆的高度AB,在离电线杆21米的C处,用高1.20米的测角仪CD测得电线杆顶端B的仰角a=30°,求电线杆AB的高.(精确到0.1米)
= AC×tana+CD
∴AB=BE+AE
∵ BE=DE×tan a
=AC×tan a
A
︶
1200米
B
C
a
30°
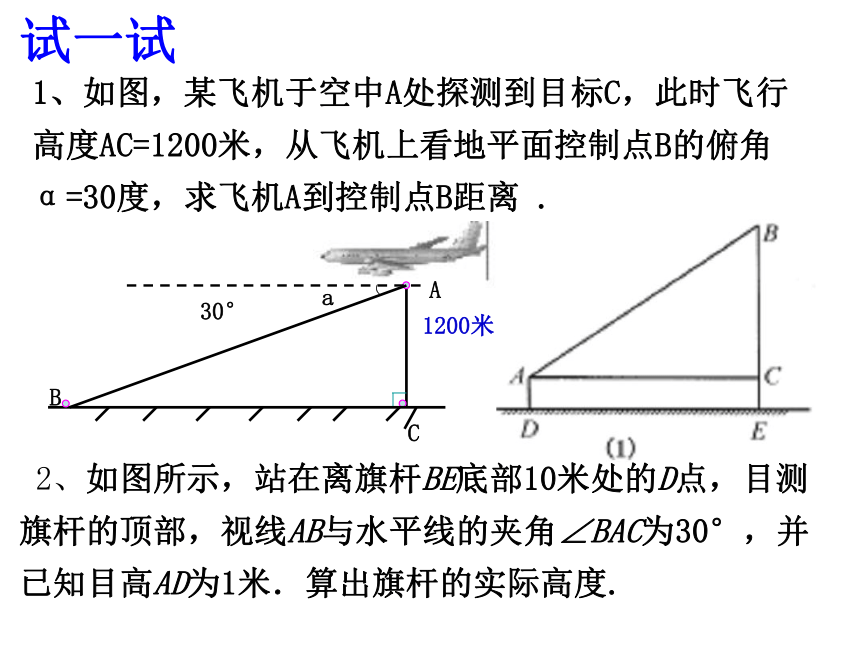
试一试
1、如图,某飞机于空中A处探测到目标C,此时飞行高度AC=1200米,从飞机上看地平面控制点B的俯角α=30度,求飞机A到控制点B距离 .
2、如图所示,站在离旗杆BE底部10米处的D点,目测旗杆的顶部,视线AB与水平线的夹角∠BAC为30°,并已知目高AD为1米.算出旗杆的实际高度.
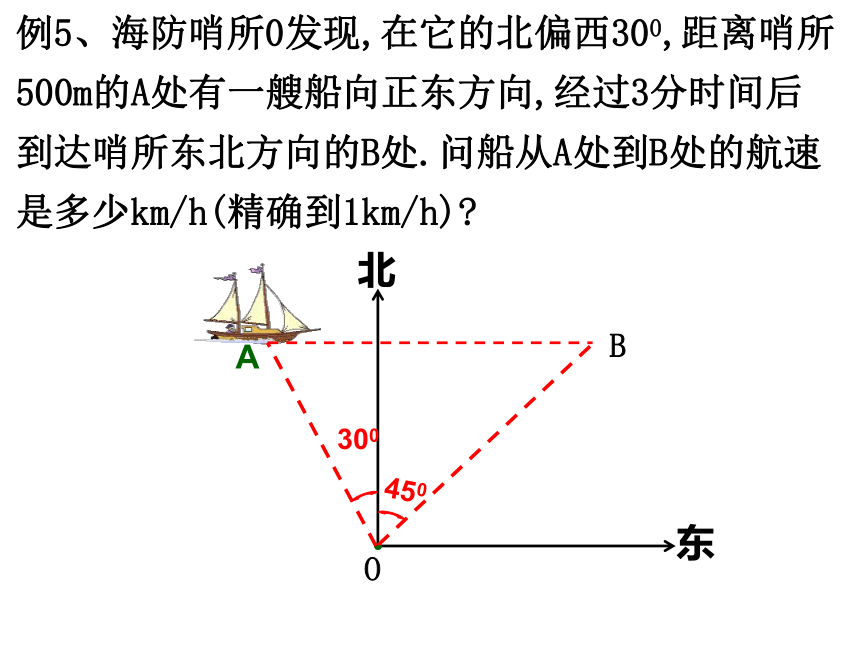
例5、海防哨所0发现,在它的北偏西300,距离哨所500m的A处有一艘船向正东方向,经过3分时间后到达哨所东北方向的B处.问船从A处到B处的航速是多少km/h(精确到1km/h)
北
东
300
450
O
A
B
500
北
东
300
450
O
A
B
C
解:
在Rt△AOC中,
OA=500m, ∠AOC=300,
∴AC=OAsin∠AOC
=500sin300
=500× =250 (m).
3
2
3
在Rt△BOC中, ∠BOC=450,
=500×0.5=250(m)
∴AC=OAcos∠AOC
∴BC=OC=
250 (m).
3
∴AB=AC+BC
=250+
250
3
∴250 (1+ ) ÷3×60
3
3
=250(1+ ) (m).
≈14000(m/h)
=14(km/h)
答:船的航速约为14km/h.
30
45
8千米
A
B
C
D
1、某船自西向东航行,在A出测得某岛在北偏东60°的
方向上,前进8千米测得某岛在船北偏东45 °的方向
上,问(1)轮船行到何处离小岛距离最近?
(2)轮船要继续前进多少千米?
做一做
α
β
24m
D
A
C
B
分析:
过D作DE∥BC,
E
问题可化归为解Rt△ABC和Rt△AED.
例6、如图,两建筑物的水平距离BC为24米,从点A测得点D 的俯角a=300,测得点C 的俯角β=60°,求AB 和CD 两座建筑物的高.(结果保留根号)
F
已知:BC=24m, ∠α=300, ∠β=600.
求:AB,CD的高.
解:
过D作DE∥BC,则DE⊥AB,
E
在Rt△ABC中,
∠ACB=∠FAC=600,
∴AB=BC·tan∠ACB
在△ADE中,
∠ADE=∠DAF=300,
DE=BC=24,
∴AE=DE·tan∠ADE
3
=24·tan300=8
=24tan600=24
3
※※※※※※※※※※※※※※※※
∴CD=AB-AE
=24 -8
3
3
=16
3
答:两座建筑物的高分别为24 m和16 m.
3
3
F
E
A
30°
15m
2、小华去实验楼做实验, 两幢实验楼的高度AB=CD=20m, 两楼间的距离BC=15m,已知太阳光与水平线的夹角为30°,求南楼的影子在北楼上有多高?
北
A
B
D
C
20m
15m
E
F
南
练一练
探究活动
C
A
B
思考:当三角形变成平行四边形时,平行四边形的两邻边分别为a,b,这组邻边所夹的锐角为α时,则它的面积能否用这三个已知量来表示呢?
S= ab sina
如图, △在ABC中, ∠A为锐角,sina= , AB+AC=6cm,设AC=xcm, △ABC的面积为ycm2.
(1)求y关于x的函数关系式和自变量x的取值范围;
(2)何时△ABC的面积最大,最大面积为多少
D
通过实践了解仰角和俯角在解直角三角形中的作用。
解直角三角形的应用是数学中的应用问题,反映现实领域特征的问题情景,它包含着一定的数学概念、方法和结果。
通过对实际问题的抽象提炼,分辨出解直角三角形的基本模式,用常规的代数方法解决问题。
2.两种情况:
解直角三角形,只有下面两种情况:
(1)已知两条边;
(2)已知一条边和一个锐角
1.解直角三角形.
在直角三角形中,由已知元素求出未知元素的过程,叫做解直角三角形.
如图,在进行测量时,
从下向上看,视线与水平线的夹角叫做仰角;
从上往下看,视线与水平线的夹角叫做俯角.
知识小贴士
例1
如图,为了测量电线杆的高度AB,在离电线杆21米的C处,用高1.20米的测角仪CD测得电线杆顶端B的仰角a=30°,求电线杆AB的高.(精确到0.1米)
你会解吗?
例1
在Rt△BDE中,
解:
如图,为了测量电线杆的高度AB,在离电线杆21米的C处,用高1.20米的测角仪CD测得电线杆顶端B的仰角a=30°,求电线杆AB的高.(精确到0.1米)
= AC×tana+CD
∴AB=BE+AE
∵ BE=DE×tan a
=AC×tan a
A
︶
1200米
B
C
a
30°
试一试
1、如图,某飞机于空中A处探测到目标C,此时飞行高度AC=1200米,从飞机上看地平面控制点B的俯角α=30度,求飞机A到控制点B距离 .
2、如图所示,站在离旗杆BE底部10米处的D点,目测旗杆的顶部,视线AB与水平线的夹角∠BAC为30°,并已知目高AD为1米.算出旗杆的实际高度.
例5、海防哨所0发现,在它的北偏西300,距离哨所500m的A处有一艘船向正东方向,经过3分时间后到达哨所东北方向的B处.问船从A处到B处的航速是多少km/h(精确到1km/h)
北
东
300
450
O
A
B
500
北
东
300
450
O
A
B
C
解:
在Rt△AOC中,
OA=500m, ∠AOC=300,
∴AC=OAsin∠AOC
=500sin300
=500× =250 (m).
3
2
3
在Rt△BOC中, ∠BOC=450,
=500×0.5=250(m)
∴AC=OAcos∠AOC
∴BC=OC=
250 (m).
3
∴AB=AC+BC
=250+
250
3
∴250 (1+ ) ÷3×60
3
3
=250(1+ ) (m).
≈14000(m/h)
=14(km/h)
答:船的航速约为14km/h.
30
45
8千米
A
B
C
D
1、某船自西向东航行,在A出测得某岛在北偏东60°的
方向上,前进8千米测得某岛在船北偏东45 °的方向
上,问(1)轮船行到何处离小岛距离最近?
(2)轮船要继续前进多少千米?
做一做
α
β
24m
D
A
C
B
分析:
过D作DE∥BC,
E
问题可化归为解Rt△ABC和Rt△AED.
例6、如图,两建筑物的水平距离BC为24米,从点A测得点D 的俯角a=300,测得点C 的俯角β=60°,求AB 和CD 两座建筑物的高.(结果保留根号)
F
已知:BC=24m, ∠α=300, ∠β=600.
求:AB,CD的高.
解:
过D作DE∥BC,则DE⊥AB,
E
在Rt△ABC中,
∠ACB=∠FAC=600,
∴AB=BC·tan∠ACB
在△ADE中,
∠ADE=∠DAF=300,
DE=BC=24,
∴AE=DE·tan∠ADE
3
=24·tan300=8
=24tan600=24
3
※※※※※※※※※※※※※※※※
∴CD=AB-AE
=24 -8
3
3
=16
3
答:两座建筑物的高分别为24 m和16 m.
3
3
F
E
A
30°
15m
2、小华去实验楼做实验, 两幢实验楼的高度AB=CD=20m, 两楼间的距离BC=15m,已知太阳光与水平线的夹角为30°,求南楼的影子在北楼上有多高?
北
A
B
D
C
20m
15m
E
F
南
练一练
探究活动
C
A
B
思考:当三角形变成平行四边形时,平行四边形的两邻边分别为a,b,这组邻边所夹的锐角为α时,则它的面积能否用这三个已知量来表示呢?
S= ab sina
如图, △在ABC中, ∠A为锐角,sina= , AB+AC=6cm,设AC=xcm, △ABC的面积为ycm2.
(1)求y关于x的函数关系式和自变量x的取值范围;
(2)何时△ABC的面积最大,最大面积为多少
D
通过实践了解仰角和俯角在解直角三角形中的作用。
解直角三角形的应用是数学中的应用问题,反映现实领域特征的问题情景,它包含着一定的数学概念、方法和结果。
通过对实际问题的抽象提炼,分辨出解直角三角形的基本模式,用常规的代数方法解决问题。
