浙教版初中数学八年级上册 1.1 认识三角形 课件(26张)
文档属性
| 名称 | 浙教版初中数学八年级上册 1.1 认识三角形 课件(26张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 597.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-21 00:00:00 | ||
图片预览

文档简介
认识三角形(2)
1.1
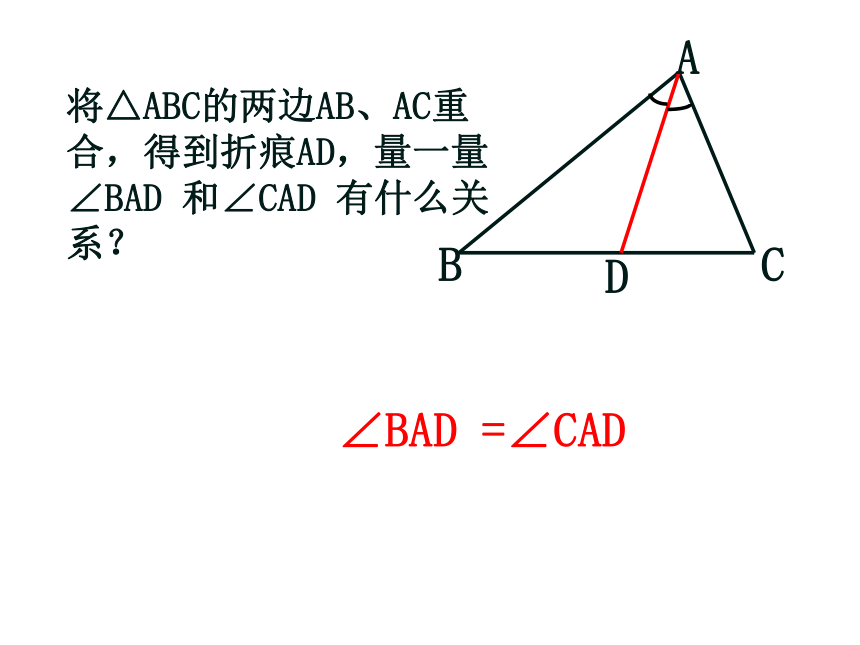
A
D
C
B
∠BAD =∠CAD
将△ABC的两边AB、AC重合,得到折痕AD,量一量∠BAD 和∠CAD 有什么关系?
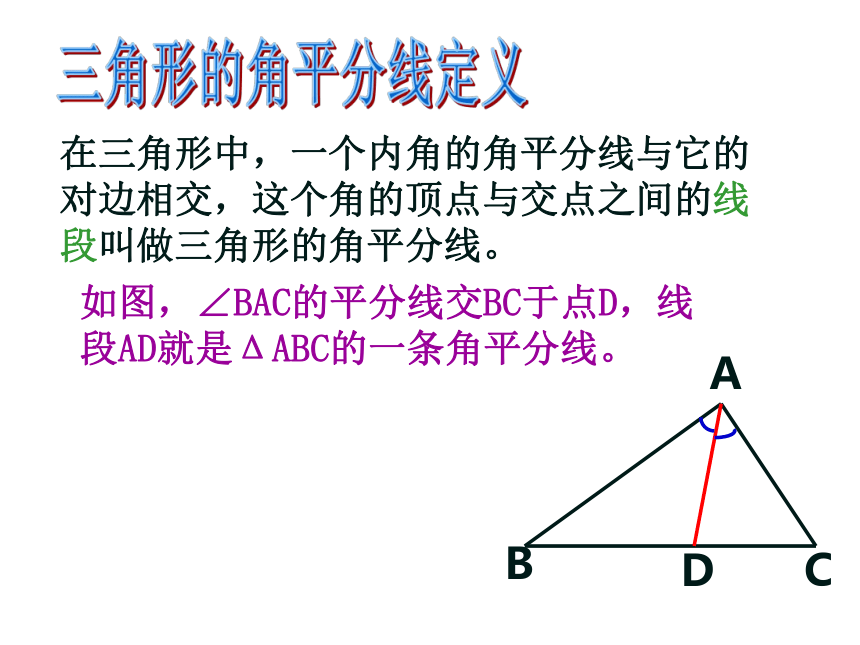
三角形的角平分线定义
在三角形中,一个内角的角平分线与它的对边相交,这个角的顶点与交点之间的线段叫做三角形的角平分线。
C
A
D
B
如图,∠BAC的平分线交BC于点D,线段AD就是ΔABC的一条角平分线。
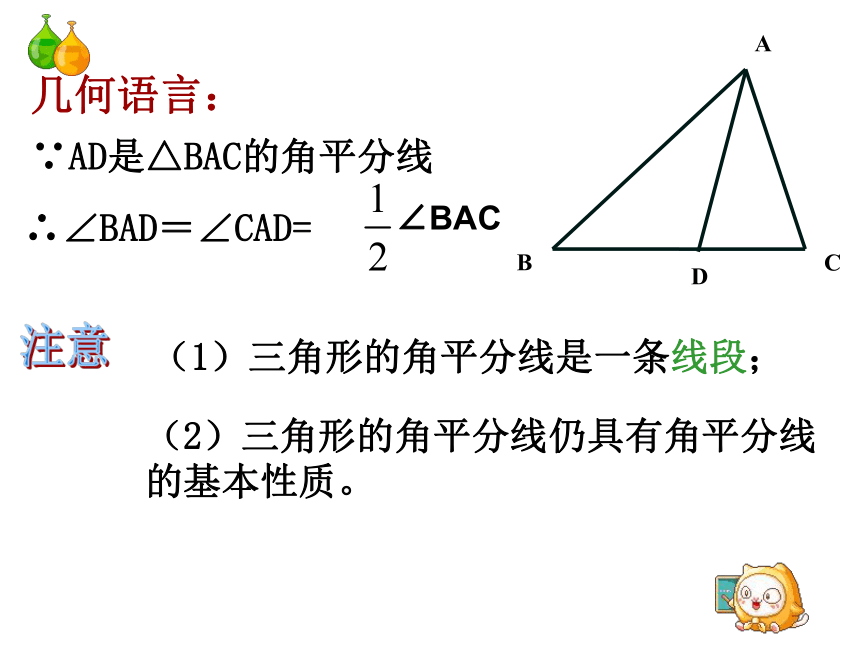
A
B
C
D
几何语言:
(1)三角形的角平分线是一条线段;
(2)三角形的角平分线仍具有角平分线的基本性质。
注意
∵AD是△BAC的角平分线
∴∠BAD=∠CAD=
∠BAC
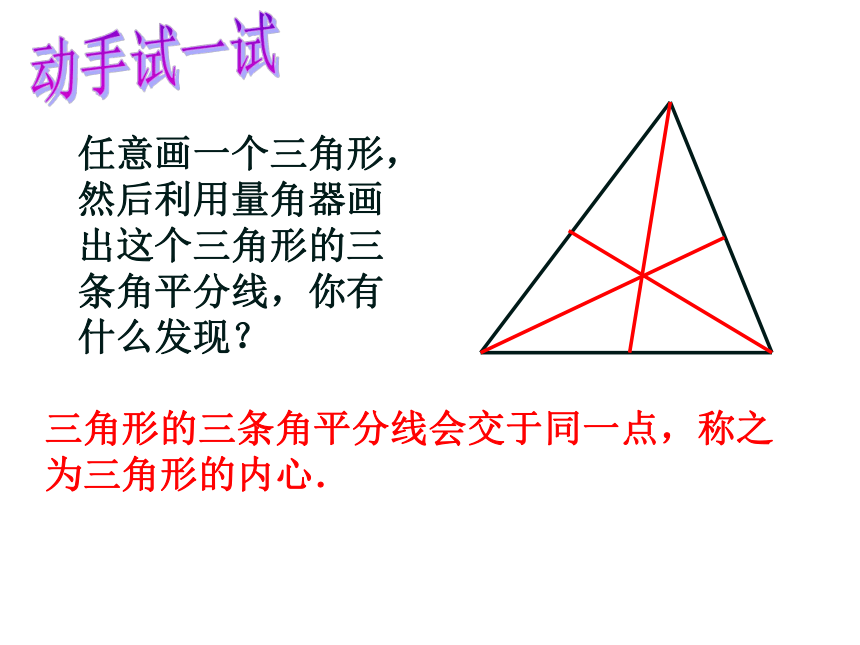
动手试一试
任意画一个三角形,
然后利用量角器画
出这个三角形的三
条角平分线,你有
什么发现?
三角形的三条角平分线会交于同一点,称之为三角形的内心.
A
D
C
B
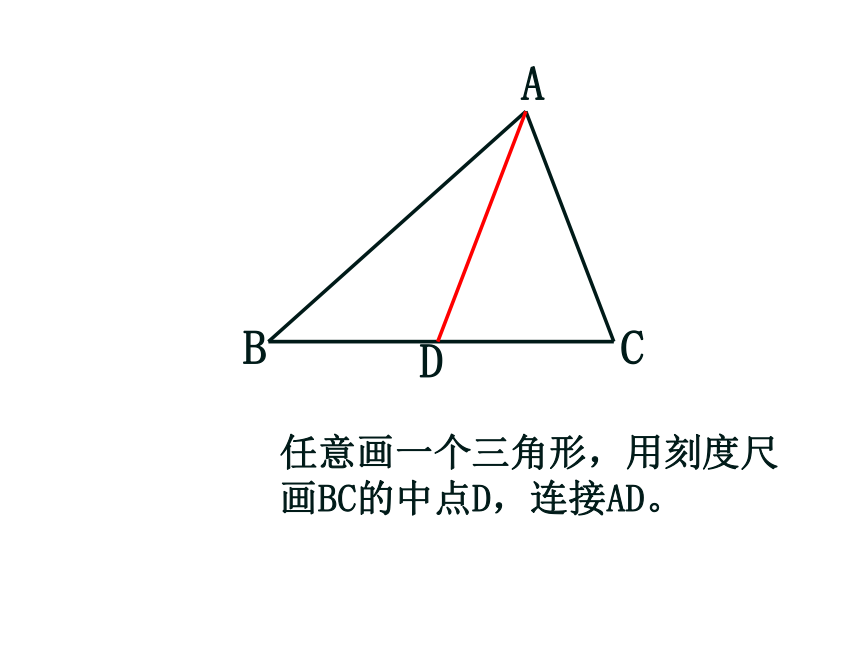
任意画一个三角形,用刻度尺
画BC的中点D,连接AD。
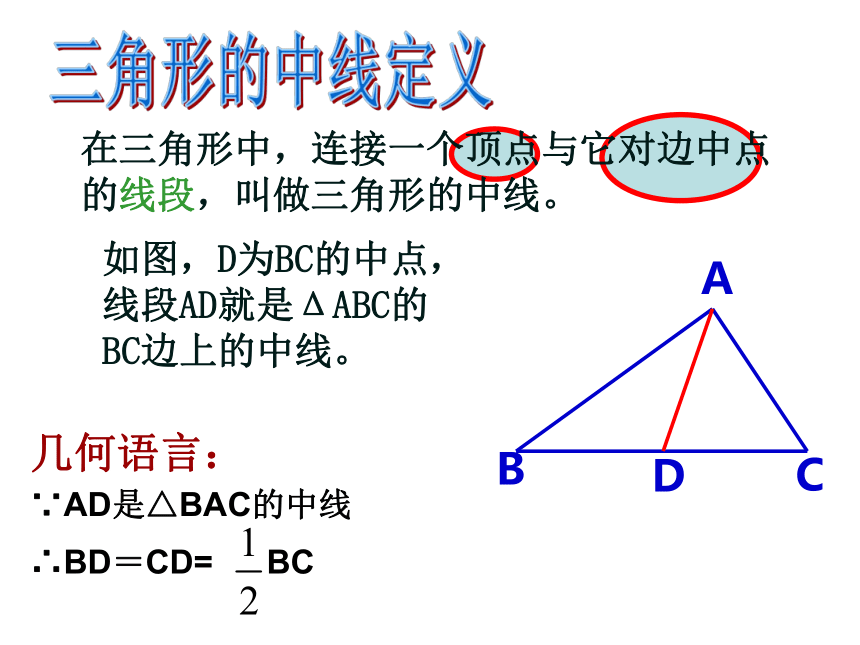
三角形的中线定义
在三角形中,连接一个顶点与它对边中点的线段,叫做三角形的中线。
A
C
D
B
如图,D为BC的中点,
线段AD就是ΔABC的
BC边上的中线。
几何语言:
∵AD是△BAC的中线
∴BD=CD=
BC
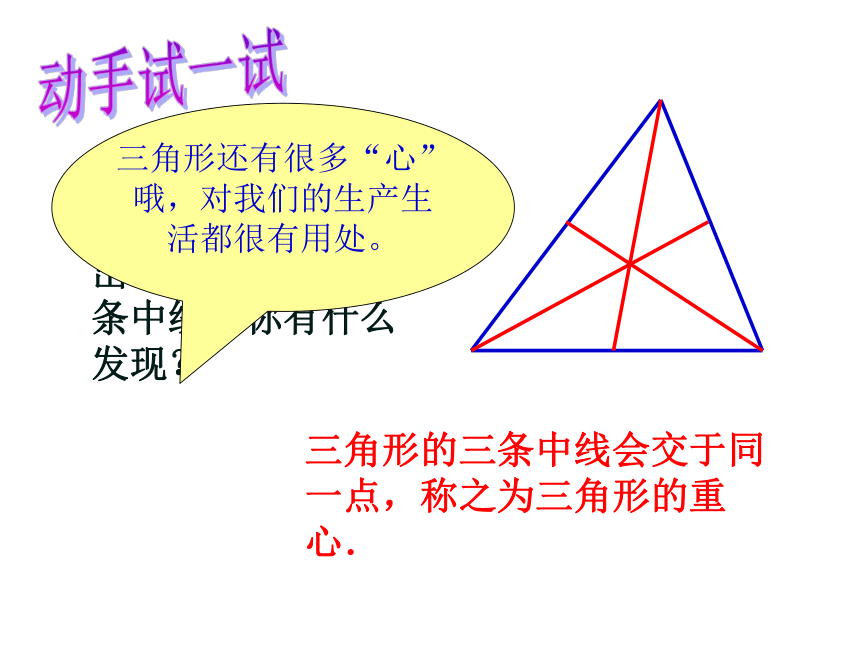
动手试一试
任意画一个三角形,
然后利用刻度尺画
出这个三角形的三
条中线,你有什么
发现?
三角形的三条中线会交于同一点,称之为三角形的重心.
三角形还有很多“心”哦,对我们的生产生活都很有用处。
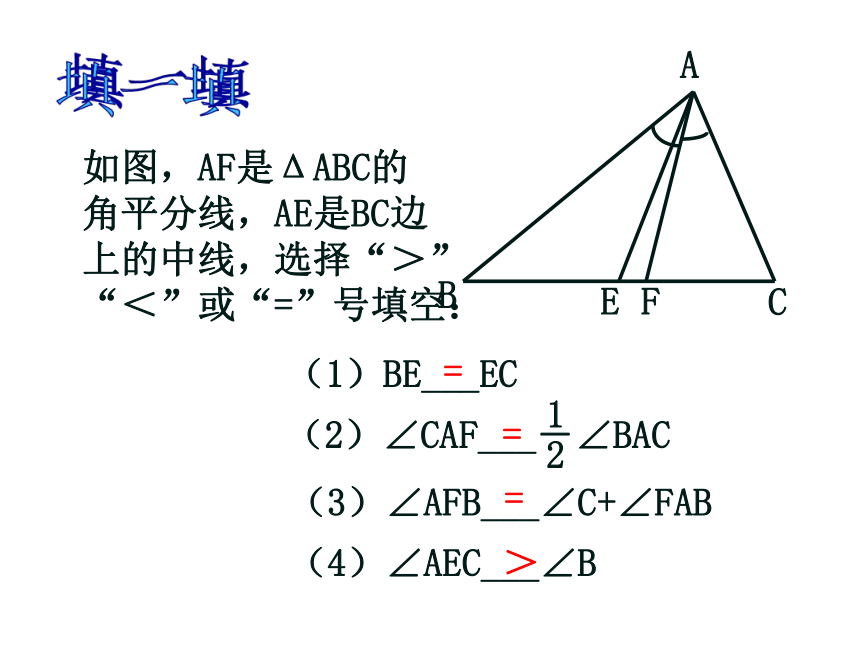
填一填
如图,AF是ΔABC的
角平分线,AE是BC边
上的中线,选择“>”
“<”或“=”号填空:
(1)BE___EC
(2)∠CAF___―∠BAC
1
2
(3)∠AFB___∠C+∠FAB
(4)∠AEC___∠B
F
E
C
B
A
=
=
=
>
C
A
B
D
如图,AD是△BAC的角平分线。已知∠B=48°,∠C=63°,求下列各角的度数:(1)∠BAD;(2)∠ADB
例1
变式1:
如图,CD是∠ ACB的平分线,∠A=30°,∠ACB=90°,求∠BDC的度数。
变式2:
在
△ABC中,∠ABC= ∠C=2 ∠A,
BD是∠ ABC的平分线,求∠A与
∠ADB的度数。
数形结合思想、方程思想
与角平分线有关的计算
从三角形的一个顶点向它的对边所在的直线作垂线,顶点和垂足之间的线段叫做三角形的高
∵ AD ⊥ BC
∴ AD是△ ABC的BC边上的高
A
B
C
D
∵ AD是△ ABC
的BC边上的高
∴ AD ⊥ BC
一个三角形
有几条高?
.
.
.
.
.
.
合作学习
用三角尺分别作如下锐角三角形ABC,直角三
角形DEF和钝角三角形PQR的各边上的高.
观察你所作的图形,比较三个三角形中三
条高的位置,与三角形之间有什么关系?
A
C
B
E
F
D
R
Q
P
高
锐角三角形
直角三角形
钝角三角形
条数
位置
垂足
交点
图形
结论
A
B
C
D
E
F
P
Q
R
3
3
3
都在三角
形内部
直角边上的高分别与另一条直角边重合,还有一条高在三角形内部
夹钝角两边上的高在三角形外部,另一条高在内部
在相应顶点的对边上
①是直角的顶点
②在斜边上
①在相应顶点的对边的延长线上
②在钝角的对边上
在三角形内部
在直角顶点
在三角形外部
4.下列各阴影部分的面积有何关系?
S乙>S甲=S丙
如图,在△ABC中,AD是△ABC的高,AE是△ABC的角平分线。已知∠BAC=82°,∠C=40°,求∠DAE的大小。
例1
E
D
C
B
A
55°
例2 在△ABC中,AE,AD分别是BC边上
的中线和高。说明△ABE的面积与
△AEC的面积相等。
解:
∵ AE是BC边上的中线
∴ BE = EC
∵
A
D
E
C
B
S △ABE= BE · AD
S △AEC= EC · AD
∴
S △AEC
S △ABE
=
三角形的中线将三角形分成面积相等的两等份
课堂达标
1.如图,在△ABC中,CD是△ABC的高.
用“>” “<” “=”填空:
(1)CD AC;
(2)∠ADC ∠A;
(3)∠A+∠ACD ∠ADC。
A
D
C
B
2、 下列关于三角形的高线的说法正确的是( )
A.直角三角形只有一条高线
B.钝角三角形 的高线都在三角形的外部
C.只有一条高线在三角形内的三角形一定是钝角三角形
D.锐角三角形的高线的交点一定在三角形的外部
<
>
=
D
3. 试把一块三角形煎饼分成大小相同
的4块,有多少种分法?
课堂达标
探究活动
如图点D,E,F 分别是△ABC的
三条边的中点.设△ABC的面积为S,
求△DEF的面积.
你可以这样考虑:
(1)连结AD. △ADC的面积是多少?
(2)由第(1)题,你能求出△DEC的面积吗?
△AEF和△FBD的面积呢?
A
C
B
E
F
D
当问题直接解决有困难时,
可以考虑从反面着手
练一练
E
A
B
C
D
(1)AD是△ ABC的BC边上的中线,则
(2)设△ ABC的面积为S,则△ ACD的面积为
(3)若点E是AC的中点,则
=
(4)若点F是AB的中点,连结EF、DF,求△ DEF的面积。
F
将这块三角形煎饼分成大小相同的6块,有几种分法?如果限定只能切三刀呢?
试一试
探究活动
如图1-16,点D,E,F 分别是△ABC的三条边的中点.设△ABC的面积为S,求△DEF的面积.
你可以这样考虑:
(1)连结AD. △ADC的面积是多少?
(2)由第(1)题,你能求出△DEC的面积吗? △AEF和△FBD的面积呢?
A
B
C
E
F
D
图1-16
回味 无穷
我的收获是 … …
我感受到了… …
我的问题存在于… …
小结
谢谢
家庭作业:
作业本(1) 1.2
新同步练习1.2
课时导航1.2
课外延伸
如图,在ΔABC中,∠A= , ∠ ABC,∠ ACB的平分线交于点O,则∠ B0C的度数为
α
60°
变式:如图,CE,CF分别是ΔABC的内角平分线和外角平分线,求∠ ECF的度数.
整体思想
1.1
A
D
C
B
∠BAD =∠CAD
将△ABC的两边AB、AC重合,得到折痕AD,量一量∠BAD 和∠CAD 有什么关系?
三角形的角平分线定义
在三角形中,一个内角的角平分线与它的对边相交,这个角的顶点与交点之间的线段叫做三角形的角平分线。
C
A
D
B
如图,∠BAC的平分线交BC于点D,线段AD就是ΔABC的一条角平分线。
A
B
C
D
几何语言:
(1)三角形的角平分线是一条线段;
(2)三角形的角平分线仍具有角平分线的基本性质。
注意
∵AD是△BAC的角平分线
∴∠BAD=∠CAD=
∠BAC
动手试一试
任意画一个三角形,
然后利用量角器画
出这个三角形的三
条角平分线,你有
什么发现?
三角形的三条角平分线会交于同一点,称之为三角形的内心.
A
D
C
B
任意画一个三角形,用刻度尺
画BC的中点D,连接AD。
三角形的中线定义
在三角形中,连接一个顶点与它对边中点的线段,叫做三角形的中线。
A
C
D
B
如图,D为BC的中点,
线段AD就是ΔABC的
BC边上的中线。
几何语言:
∵AD是△BAC的中线
∴BD=CD=
BC
动手试一试
任意画一个三角形,
然后利用刻度尺画
出这个三角形的三
条中线,你有什么
发现?
三角形的三条中线会交于同一点,称之为三角形的重心.
三角形还有很多“心”哦,对我们的生产生活都很有用处。
填一填
如图,AF是ΔABC的
角平分线,AE是BC边
上的中线,选择“>”
“<”或“=”号填空:
(1)BE___EC
(2)∠CAF___―∠BAC
1
2
(3)∠AFB___∠C+∠FAB
(4)∠AEC___∠B
F
E
C
B
A
=
=
=
>
C
A
B
D
如图,AD是△BAC的角平分线。已知∠B=48°,∠C=63°,求下列各角的度数:(1)∠BAD;(2)∠ADB
例1
变式1:
如图,CD是∠ ACB的平分线,∠A=30°,∠ACB=90°,求∠BDC的度数。
变式2:
在
△ABC中,∠ABC= ∠C=2 ∠A,
BD是∠ ABC的平分线,求∠A与
∠ADB的度数。
数形结合思想、方程思想
与角平分线有关的计算
从三角形的一个顶点向它的对边所在的直线作垂线,顶点和垂足之间的线段叫做三角形的高
∵ AD ⊥ BC
∴ AD是△ ABC的BC边上的高
A
B
C
D
∵ AD是△ ABC
的BC边上的高
∴ AD ⊥ BC
一个三角形
有几条高?
.
.
.
.
.
.
合作学习
用三角尺分别作如下锐角三角形ABC,直角三
角形DEF和钝角三角形PQR的各边上的高.
观察你所作的图形,比较三个三角形中三
条高的位置,与三角形之间有什么关系?
A
C
B
E
F
D
R
Q
P
高
锐角三角形
直角三角形
钝角三角形
条数
位置
垂足
交点
图形
结论
A
B
C
D
E
F
P
Q
R
3
3
3
都在三角
形内部
直角边上的高分别与另一条直角边重合,还有一条高在三角形内部
夹钝角两边上的高在三角形外部,另一条高在内部
在相应顶点的对边上
①是直角的顶点
②在斜边上
①在相应顶点的对边的延长线上
②在钝角的对边上
在三角形内部
在直角顶点
在三角形外部
4.下列各阴影部分的面积有何关系?
S乙>S甲=S丙
如图,在△ABC中,AD是△ABC的高,AE是△ABC的角平分线。已知∠BAC=82°,∠C=40°,求∠DAE的大小。
例1
E
D
C
B
A
55°
例2 在△ABC中,AE,AD分别是BC边上
的中线和高。说明△ABE的面积与
△AEC的面积相等。
解:
∵ AE是BC边上的中线
∴ BE = EC
∵
A
D
E
C
B
S △ABE= BE · AD
S △AEC= EC · AD
∴
S △AEC
S △ABE
=
三角形的中线将三角形分成面积相等的两等份
课堂达标
1.如图,在△ABC中,CD是△ABC的高.
用“>” “<” “=”填空:
(1)CD AC;
(2)∠ADC ∠A;
(3)∠A+∠ACD ∠ADC。
A
D
C
B
2、 下列关于三角形的高线的说法正确的是( )
A.直角三角形只有一条高线
B.钝角三角形 的高线都在三角形的外部
C.只有一条高线在三角形内的三角形一定是钝角三角形
D.锐角三角形的高线的交点一定在三角形的外部
<
>
=
D
3. 试把一块三角形煎饼分成大小相同
的4块,有多少种分法?
课堂达标
探究活动
如图点D,E,F 分别是△ABC的
三条边的中点.设△ABC的面积为S,
求△DEF的面积.
你可以这样考虑:
(1)连结AD. △ADC的面积是多少?
(2)由第(1)题,你能求出△DEC的面积吗?
△AEF和△FBD的面积呢?
A
C
B
E
F
D
当问题直接解决有困难时,
可以考虑从反面着手
练一练
E
A
B
C
D
(1)AD是△ ABC的BC边上的中线,则
(2)设△ ABC的面积为S,则△ ACD的面积为
(3)若点E是AC的中点,则
=
(4)若点F是AB的中点,连结EF、DF,求△ DEF的面积。
F
将这块三角形煎饼分成大小相同的6块,有几种分法?如果限定只能切三刀呢?
试一试
探究活动
如图1-16,点D,E,F 分别是△ABC的三条边的中点.设△ABC的面积为S,求△DEF的面积.
你可以这样考虑:
(1)连结AD. △ADC的面积是多少?
(2)由第(1)题,你能求出△DEC的面积吗? △AEF和△FBD的面积呢?
A
B
C
E
F
D
图1-16
回味 无穷
我的收获是 … …
我感受到了… …
我的问题存在于… …
小结
谢谢
家庭作业:
作业本(1) 1.2
新同步练习1.2
课时导航1.2
课外延伸
如图,在ΔABC中,∠A= , ∠ ABC,∠ ACB的平分线交于点O,则∠ B0C的度数为
α
60°
变式:如图,CE,CF分别是ΔABC的内角平分线和外角平分线,求∠ ECF的度数.
整体思想
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
