浙教版初中数学八年级上册 1.4 全等三角形课件(20张ppt)
文档属性
| 名称 | 浙教版初中数学八年级上册 1.4 全等三角形课件(20张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-21 15:25:30 | ||
图片预览





文档简介
三角形全等的判定(一)
(第一课时)
复习提问:
1.什么样的图形称为全等形?
什么样的两个三角形是全等三角形?
2.全等三角形有哪些性质?
A
D
E
B
C
例: 按下列要求作图:
画法:
1.画∠MDN=400
2.在射线DM,DN上分别截取DE=3 cm,DF=3.8cm
3.连结EF
实际操作:把△DEF剪下放到教材P26图3-19 的△ABC上,可以看到△DEF和△ABC完全重合。
如图,修补一块玻璃,问取哪一块玻璃可以使得这块新玻璃与原来的完全一样?
又例:
Ⅰ
Ⅱ
Ⅲ
有两组边和它们的夹角对应相等的一些三角形全等。
边角边公理:
简写成:“边角边”或“SAS”
说明:
为了问题研究的方便,以后常见的是寻找两个三角形全等
练习:教材P27第1题
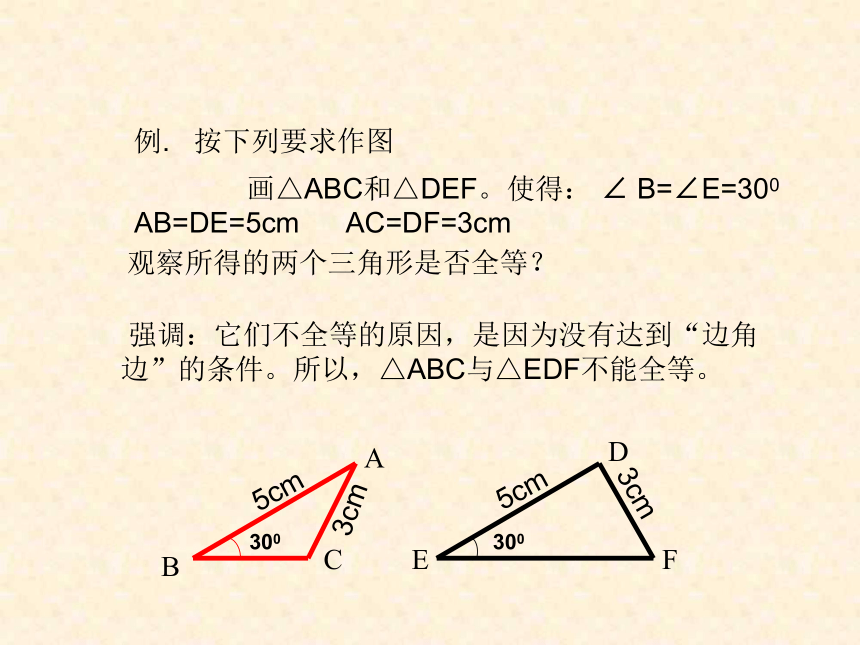
画△ABC和△DEF。使得: ∠ B=∠E=300 AB=DE=5cm AC=DF=3cm
例. 按下列要求作图
观察所得的两个三角形是否全等?
强调:它们不全等的原因,是因为没有达到“边角边”的条件。所以,△ABC与△EDF不能全等。
D
E
F
300
3cm
5cm
B
C
A
300
5cm
3cm
图 1
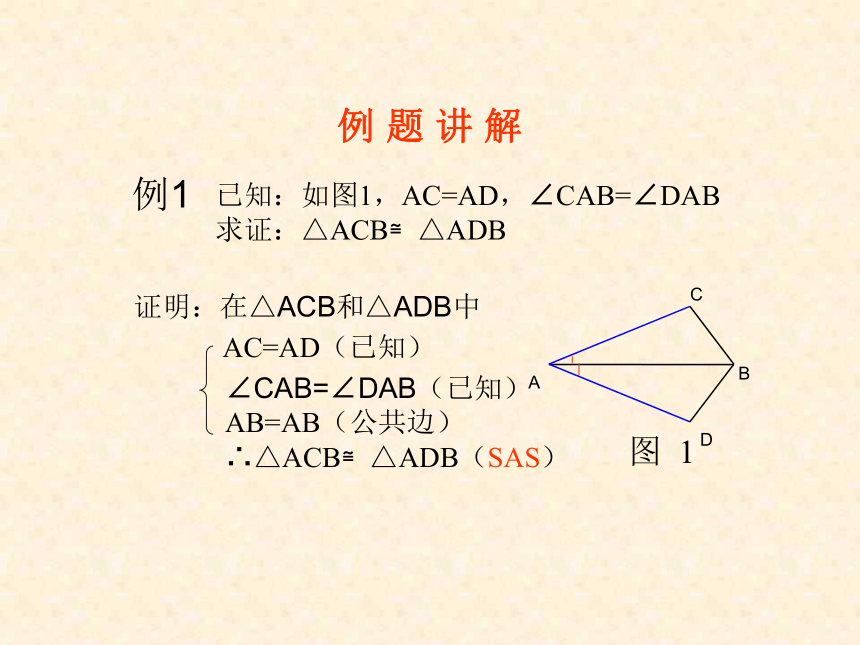
已知:如图1,AC=AD,∠CAB=∠DAB
求证:△ACB≌△ADB
AC=AD(已知)
∠CAB=∠DAB(已知)
AB=AB(公共边)
∴△ACB≌△ADB(SAS)
例1
证明:在△ACB和△ADB中
例 题 讲 解
A
B
C
D
图2
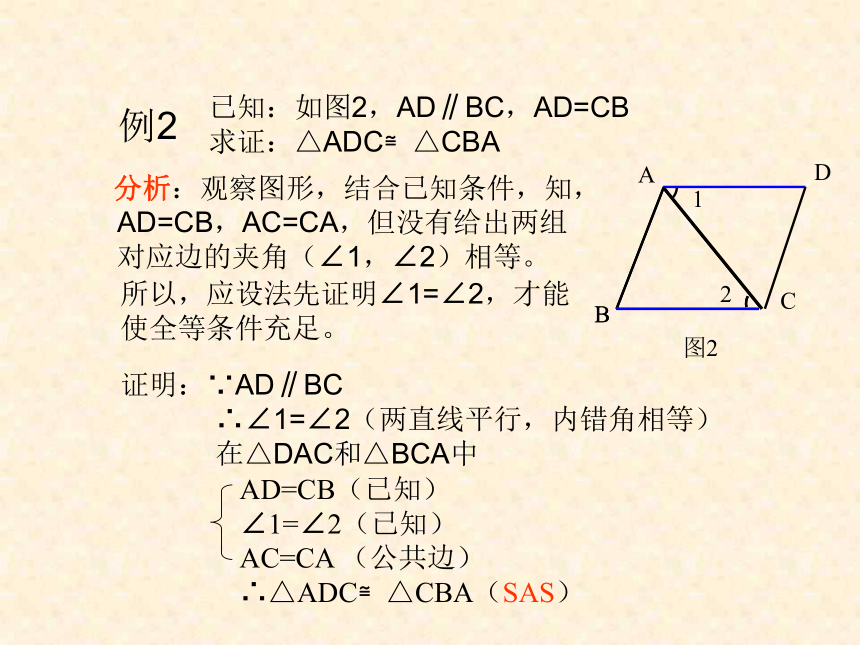
已知:如图2,AD∥BC,AD=CB
求证:△ADC≌△CBA
分析:观察图形,结合已知条件,知,
AD=CB,AC=CA,但没有给出两组对应边的夹角(∠1,∠2)相等。
所以,应设法先证明∠1=∠2,才能使全等条件充足。
AD=CB(已知)
∠1=∠2(已知)
AC=CA (公共边)
∴△ADC≌△CBA(SAS)
例2
证明:∵AD∥BC
∴∠1=∠2(两直线平行,内错角相等)
在△DAC和△BCA中
D
C
1
A
B
2
B
B
2
D
C
1
A
动 态 演 示
图3
已知:如图3 ,AD∥BC,AD=CB,AE=CF
求证:AFD≌△CEB
证明:∵AD∥BC(已知)
∴∠A=∠C(两直线平行,内错角相等)
又 AE=CF
∴AE+EF=CF+EF(等式性质)
即AF=CE
在△AFD 和△CEB 中
AD=CB(已知)
∠A=∠C(已证)
AF=CE(已证)
∴△AFD≌△CEB(SAS)
若求证∠D=∠B ,如何证明?
分析:本题已知中的前两个条件,与例2相同,但是没有另一组夹边对应相等的条件,不难发现图3是由图2平移而得。利用AE=CF,可得:AF=CE
变式训练1.
问:
A
D
B
E
F
C
B
2
D
C
1
A
动 态 演 示
练习:已知:如图4,点A、B、C、D在同一条直线上,AC=DB,AE=DF,EA⊥AD,BC⊥AC,垂足分别为A、D
图4
求证:(1)△EAB≌△FDC、(2)DF= AE
B
E
C
D
F
A
解 题 小 结:
解题思路
1、根据“边角边(SAS)”条件,可证明两个三角形全等;
2、再由“全等”作为过渡的条件,得到对应边等或对应角等;
1
2
图5
变式训练2 已知:如图5:AB=AC,AD=AE,∠1=∠2
求证:△ABD≌△ACE
证明:∵∠1=∠2(已知)
∴∠1+∠BAE = ∠2+∠BAE(等式性质)
即 ∠CAE= ∠BAD
在△CAE和△BAD 中
AC=AB(已知)
∠CAE=∠BAD(已证)
AE=AD
∴△ABD≌△ACE(ASA)
分析:两组对应夹边已知,缺少
对应夹角相等的条件。
由∠BAE 是两个三角形的
公共部分,可得:∠CAE=∠BAD。
变式训练2:拓 展
(1)求证:∠B=∠D
(2)若△ACE绕点A逆时针旋转,使∠1=900时,直线EC,BD的位置关系如何?给出证明。
当∠EAD 为平角时呢?
图5
D
B
A
E
C
M
F
已知:如图5:AB=AC,AD=AE,∠1=∠2
1
2
解 题 小 结:
解题思路
1、根据“边角边(SAS)”条件,可证明两个三角形全等;
2、再由“全等”作为过渡的条件,得到对应边等或对应角等;
3、由“边”等,再根据等式性质得到其它线段相等;由“角”等,再证明两直线平行、两直线垂直或延伸的外角和等变换。
1.在证明三角形全等时,要善于观察图形,运用已学知识挖出隐含条件。
总结概括,知识拓宽
2.明确全等三角形“边角边”公理的运用方法。
四.拓展练习,布置作业
1.作业:教材:P33 第7、8题
2 .思考:已知:AD为△ABC 的中线。
求证:AB+AC>2AD
3.预习:全等三角形判定(二)
再 见
(第一课时)
复习提问:
1.什么样的图形称为全等形?
什么样的两个三角形是全等三角形?
2.全等三角形有哪些性质?
A
D
E
B
C
例: 按下列要求作图:
画法:
1.画∠MDN=400
2.在射线DM,DN上分别截取DE=3 cm,DF=3.8cm
3.连结EF
实际操作:把△DEF剪下放到教材P26图3-19 的△ABC上,可以看到△DEF和△ABC完全重合。
如图,修补一块玻璃,问取哪一块玻璃可以使得这块新玻璃与原来的完全一样?
又例:
Ⅰ
Ⅱ
Ⅲ
有两组边和它们的夹角对应相等的一些三角形全等。
边角边公理:
简写成:“边角边”或“SAS”
说明:
为了问题研究的方便,以后常见的是寻找两个三角形全等
练习:教材P27第1题
画△ABC和△DEF。使得: ∠ B=∠E=300 AB=DE=5cm AC=DF=3cm
例. 按下列要求作图
观察所得的两个三角形是否全等?
强调:它们不全等的原因,是因为没有达到“边角边”的条件。所以,△ABC与△EDF不能全等。
D
E
F
300
3cm
5cm
B
C
A
300
5cm
3cm
图 1
已知:如图1,AC=AD,∠CAB=∠DAB
求证:△ACB≌△ADB
AC=AD(已知)
∠CAB=∠DAB(已知)
AB=AB(公共边)
∴△ACB≌△ADB(SAS)
例1
证明:在△ACB和△ADB中
例 题 讲 解
A
B
C
D
图2
已知:如图2,AD∥BC,AD=CB
求证:△ADC≌△CBA
分析:观察图形,结合已知条件,知,
AD=CB,AC=CA,但没有给出两组对应边的夹角(∠1,∠2)相等。
所以,应设法先证明∠1=∠2,才能使全等条件充足。
AD=CB(已知)
∠1=∠2(已知)
AC=CA (公共边)
∴△ADC≌△CBA(SAS)
例2
证明:∵AD∥BC
∴∠1=∠2(两直线平行,内错角相等)
在△DAC和△BCA中
D
C
1
A
B
2
B
B
2
D
C
1
A
动 态 演 示
图3
已知:如图3 ,AD∥BC,AD=CB,AE=CF
求证:AFD≌△CEB
证明:∵AD∥BC(已知)
∴∠A=∠C(两直线平行,内错角相等)
又 AE=CF
∴AE+EF=CF+EF(等式性质)
即AF=CE
在△AFD 和△CEB 中
AD=CB(已知)
∠A=∠C(已证)
AF=CE(已证)
∴△AFD≌△CEB(SAS)
若求证∠D=∠B ,如何证明?
分析:本题已知中的前两个条件,与例2相同,但是没有另一组夹边对应相等的条件,不难发现图3是由图2平移而得。利用AE=CF,可得:AF=CE
变式训练1.
问:
A
D
B
E
F
C
B
2
D
C
1
A
动 态 演 示
练习:已知:如图4,点A、B、C、D在同一条直线上,AC=DB,AE=DF,EA⊥AD,BC⊥AC,垂足分别为A、D
图4
求证:(1)△EAB≌△FDC、(2)DF= AE
B
E
C
D
F
A
解 题 小 结:
解题思路
1、根据“边角边(SAS)”条件,可证明两个三角形全等;
2、再由“全等”作为过渡的条件,得到对应边等或对应角等;
1
2
图5
变式训练2 已知:如图5:AB=AC,AD=AE,∠1=∠2
求证:△ABD≌△ACE
证明:∵∠1=∠2(已知)
∴∠1+∠BAE = ∠2+∠BAE(等式性质)
即 ∠CAE= ∠BAD
在△CAE和△BAD 中
AC=AB(已知)
∠CAE=∠BAD(已证)
AE=AD
∴△ABD≌△ACE(ASA)
分析:两组对应夹边已知,缺少
对应夹角相等的条件。
由∠BAE 是两个三角形的
公共部分,可得:∠CAE=∠BAD。
变式训练2:拓 展
(1)求证:∠B=∠D
(2)若△ACE绕点A逆时针旋转,使∠1=900时,直线EC,BD的位置关系如何?给出证明。
当∠EAD 为平角时呢?
图5
D
B
A
E
C
M
F
已知:如图5:AB=AC,AD=AE,∠1=∠2
1
2
解 题 小 结:
解题思路
1、根据“边角边(SAS)”条件,可证明两个三角形全等;
2、再由“全等”作为过渡的条件,得到对应边等或对应角等;
3、由“边”等,再根据等式性质得到其它线段相等;由“角”等,再证明两直线平行、两直线垂直或延伸的外角和等变换。
1.在证明三角形全等时,要善于观察图形,运用已学知识挖出隐含条件。
总结概括,知识拓宽
2.明确全等三角形“边角边”公理的运用方法。
四.拓展练习,布置作业
1.作业:教材:P33 第7、8题
2 .思考:已知:AD为△ABC 的中线。
求证:AB+AC>2AD
3.预习:全等三角形判定(二)
再 见
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
