浙教版初中数学八年级上册1.1 认识三角形 课件(19张)
文档属性
| 名称 | 浙教版初中数学八年级上册1.1 认识三角形 课件(19张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 677.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-21 00:00:00 | ||
图片预览

文档简介
11.1.2 三角形的高 .中线与角平分线
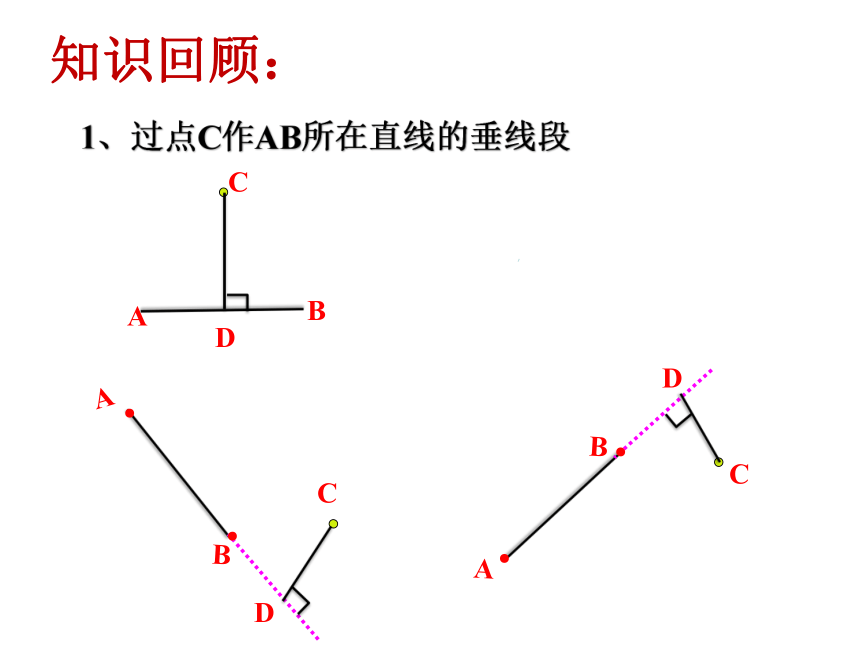
知识回顾:
1、过点C作AB所在直线的垂线段
A
B
C
D
A
B
C
D
A
B
D
C
●
●
●
●
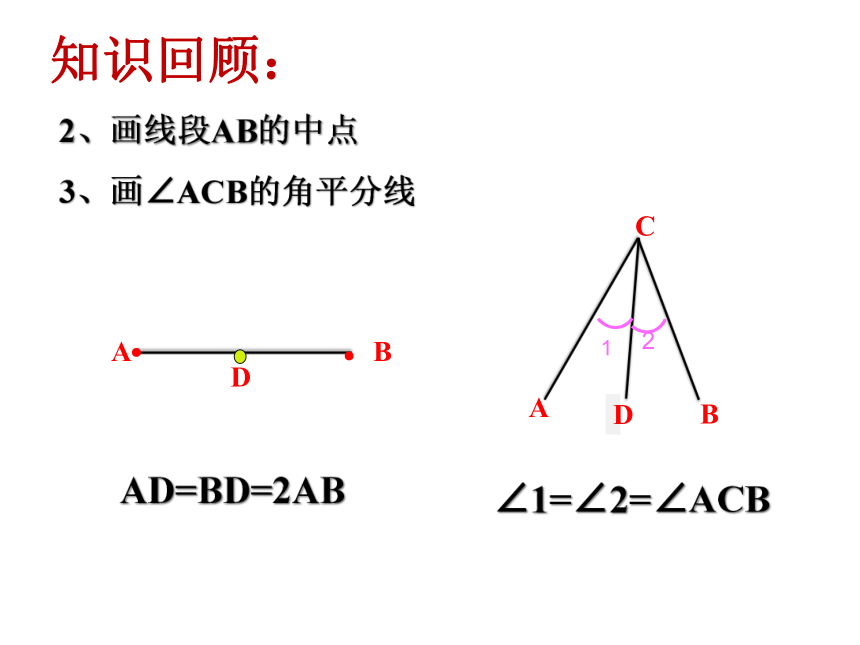
知识回顾:
2、画线段AB的中点
3、画∠ACB的角平分线
A
B
D
A
B
D
C
︶
︶
∠1=∠2=∠ACB
AD=BD=2AB
2
1
●
●
A
B
C
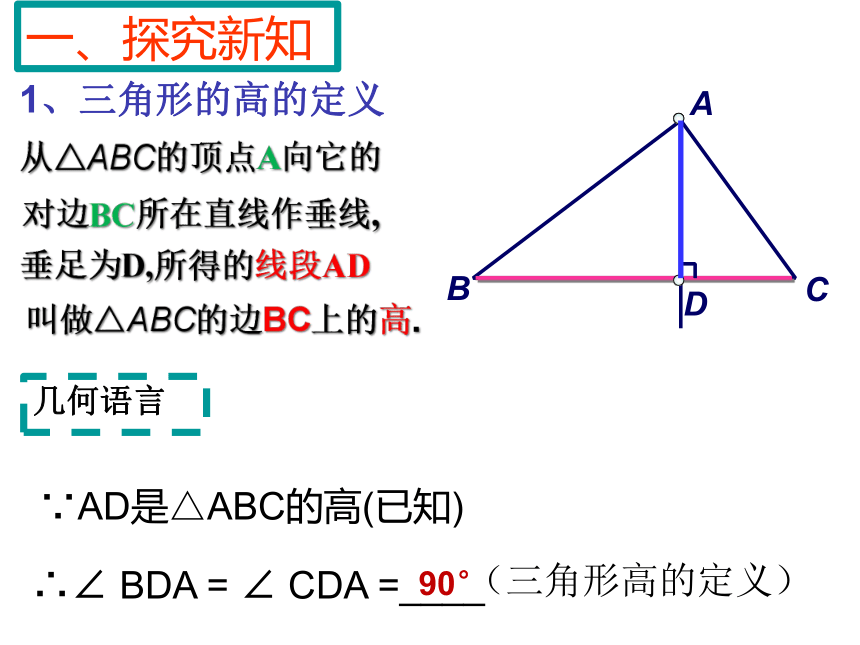
从△ABC的顶点A向它的
对边BC所在直线作垂线,
D
叫做△ABC的边BC上的高.
几何语言
∵AD是△ABC的高(已知)
90°
∴∠ BDA = ∠ CDA =____
(三角形高的定义)
垂足为D,所得的线段AD
1、三角形的高的定义
一、探究新知
A
C
B
●
●
D
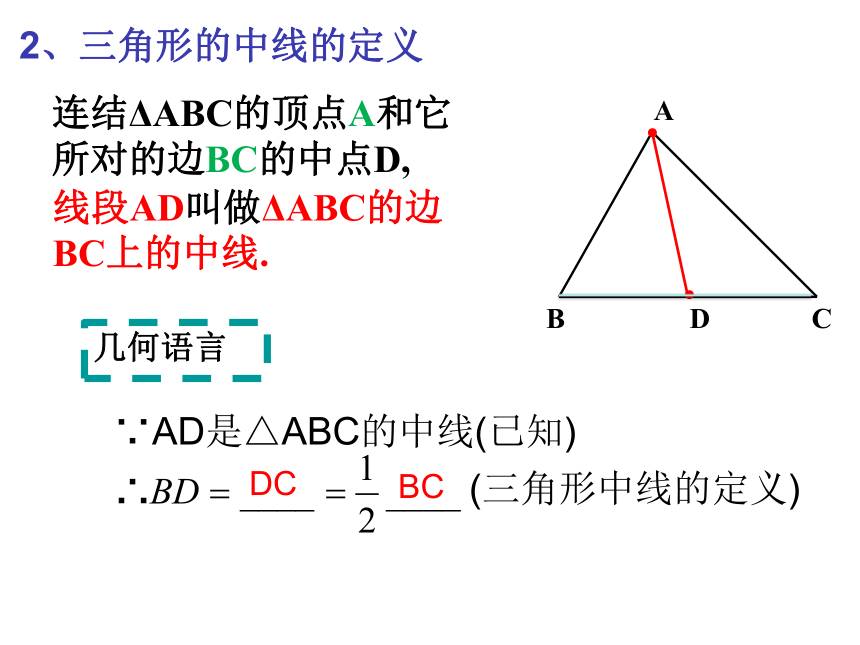
连结ΔABC的顶点A和它所对的边BC的中点D,
线段AD叫做ΔABC的边BC上的中线.
几何语言
∵AD是△ABC的中线(已知)
∴
DC
BC
(三角形中线的定义)
2、三角形的中线的定义
A
C
B
D
●
●
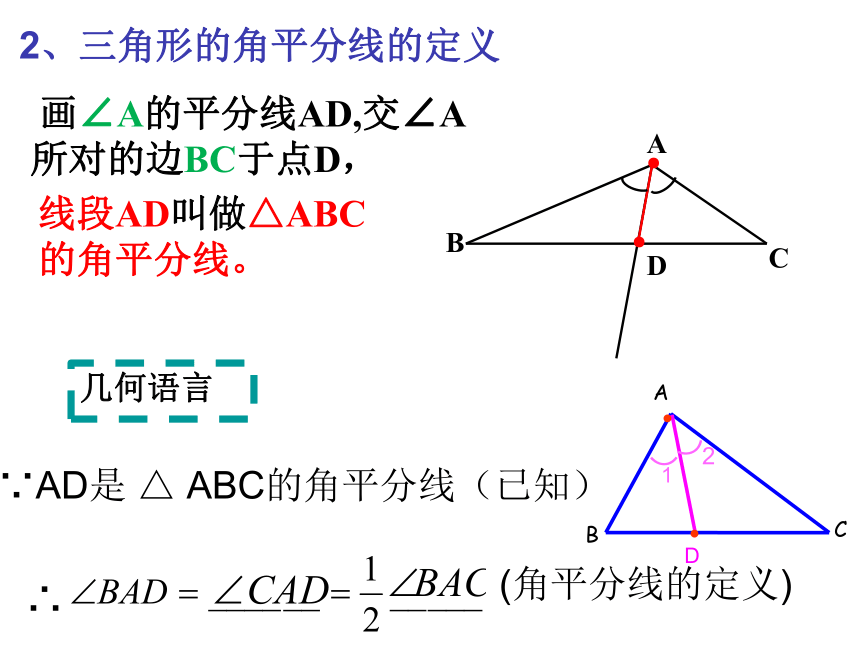
画∠A的平分线AD,交∠A所对的边BC于点D,
线段AD叫做△ABC
的角平分线。
几何语言
∵AD是 △ ABC的角平分线(已知)
A
B
C
D
●
●
︶
︶
1
2
∴
(角平分线的定义)
2、三角形的角平分线的定义
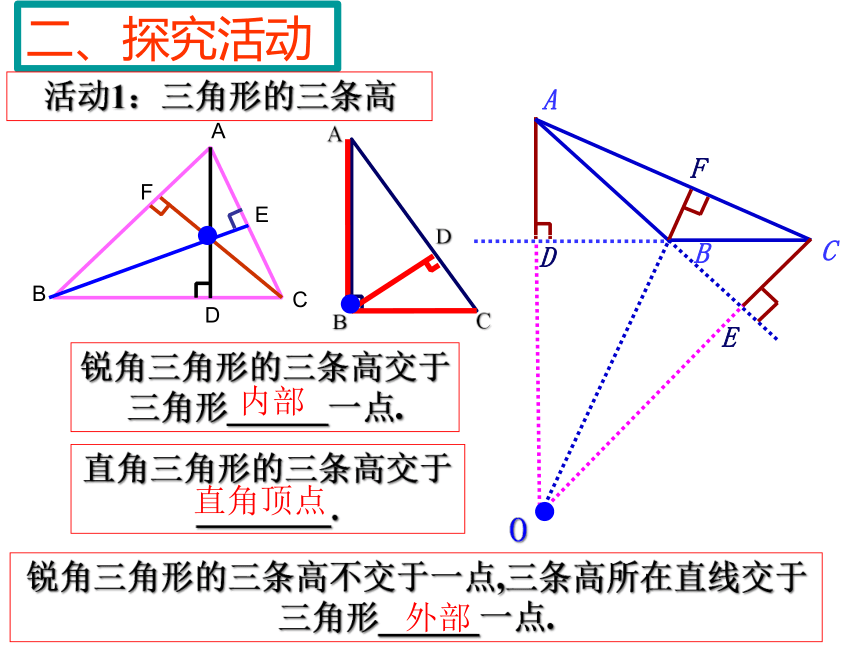
锐角三角形的三条高交于三角形______一点.
直角三角形的三条高交于________.
锐角三角形的三条高不交于一点,三条高所在直线交于三角形______一点.
二、探究活动
内部
直角顶点
外部
A
B
C
D
E
F
A
B
C
D
O
A
B
C
D
E
F
活动1:三角形的三条高
分别指出图中△ABC 的三条高。
AB
CB
A
B
C
D
E
F
A
B
C
D
BD
CE
AD
直角边BC边上的
高是 ;
直角边AB边上的
高是 ;
斜边AC边上的
高是 ;
AB边上的高是 ;
BC边上的高是 ;
CA边上的高是 ;
BF
活动1:三角形的三条高
E
观察下列三个图形你有什么发现?
三角形的三条中线交于三角形_______一点.
A
C
B
●
●
D
E
F
●
●
●
●
●
●
●
D
D
F
E
三角形的三条中线的交点叫做三角形的_______.
A
A
B
B
F
C
C
●
●
●
●
●
●
●
●
●
●
●
●
活动2:三角形的中线
内部
重心
如图1-15,在△ABC中,AE是它的中线,AD是它的高线,则△ABE的面积与△AEC的面积的大小有怎样的关系?
A
B
D
E
C
三角形的中线把三角形分成两个面积相等的三角形。
解∵AE是BC边上的中线(已知)
∴ BE = EC(三角形中线的定义)
∴
∵
三角形中线性质:
活动2:三角形的中线
中线的性质
三角形的中线把三角形分成两个面积相等的三角形。
∵AE是BC边上的中线(已知)
∴
几何语言
活动2:三角形的中线
A
B
E
C
观察下列三个图形你有什么发现?
三角形的三条角平分线在三角形的_____交于一点
●
D
F
A
B
A
C
A
C
B
D
●
●
F
E
●
●
●
●
●
E
●
D
E
B
F
C
●
●
●
●
●
●
●
●
●
●
●
●
活动3:三角形的角平分线
内部
拓展练习
达标检测
2、三角形的下列线段中,能将三角形的面积分成相等的两部分的是( )
A.中线 B.角平分线
C.高 D. 以上答案均正确
1、下列各组图形中,哪一组图形中AD是△ABC 的高( )
A
D
C
B
A
B
C
D
A
B
C
D
A
B
C
D
(A)
(B)
(C)
(D)
D
A
达标检测
3、图中共有 个三角形,若BC=CD=DE,
则AC,AD分别是______ ,____的中线.
A
B
E
D
C
6
△ABD
△ACE
4、如图,在ΔABC中,AE是中线,AD是角平分线,AF是高。填空:
(1)BE= = ;
(2)∠BAD= = ;
(3)∠AFB= =90°;
(4)SΔABC= 。
CE
BC
∠CAD
∠BAC
∠AFC
BC?AF
达标检测
拓展提升
1、如图所示,已知AD是△ABC的边BC上的中线.
(1)作出△ABD的边BD上的高.
(2)若△ABC的面积为10,求△ADC的面积.
(3)若△ABD的面积为6,且BD边上的高为3,求BC的长.
A
B
C
D
解:(1)如图所示:
E
A
B
C
D
E
(2)∵AD是△ABC的边BC上的
∴△ADC的面积
= △ABC的面积=5.
中线,△ABC的面积为10,
(3)∵AD是△ABC的边BC上的
∴△ABC的面积为12,
∵BD边上的高为3,
∴BC=12×2÷3=8
中线,△ABD的面积为6,
(2)若△ABC的面积为10,求△ADC的面积.
(3)若△ABD的面积为6,且BD边上的高为3,求BC的长.
三角形的
重要线段
概念
图形
表示法
三角形
的高线
从三角形的一个顶点向它的对边所在的直线作垂线,顶点和垂足之间的线段
∵AD是△ABC的BC上的高线.
∴AD⊥BC
∠ADB=∠ADC=90°.
三角形
的中线
三角形中,连结一个顶点和它对边中的
线段
∵ AD是△ABC的BC上的中线.
∴ BD=CD= ?BC.
三角形的
角平分线
三角形一个内角的平分线与它的对边相交,这个角顶点与交点之间的线段
∵.AD是△ABC的∠BAC的平分线
∴ ∠1=∠2= ? ∠BAC
小结
今天你学习了什么?
向着目标
作业
课本P5 第2题
完成《数学基础训练》的基础达标
知识回顾:
1、过点C作AB所在直线的垂线段
A
B
C
D
A
B
C
D
A
B
D
C
●
●
●
●
知识回顾:
2、画线段AB的中点
3、画∠ACB的角平分线
A
B
D
A
B
D
C
︶
︶
∠1=∠2=∠ACB
AD=BD=2AB
2
1
●
●
A
B
C
从△ABC的顶点A向它的
对边BC所在直线作垂线,
D
叫做△ABC的边BC上的高.
几何语言
∵AD是△ABC的高(已知)
90°
∴∠ BDA = ∠ CDA =____
(三角形高的定义)
垂足为D,所得的线段AD
1、三角形的高的定义
一、探究新知
A
C
B
●
●
D
连结ΔABC的顶点A和它所对的边BC的中点D,
线段AD叫做ΔABC的边BC上的中线.
几何语言
∵AD是△ABC的中线(已知)
∴
DC
BC
(三角形中线的定义)
2、三角形的中线的定义
A
C
B
D
●
●
画∠A的平分线AD,交∠A所对的边BC于点D,
线段AD叫做△ABC
的角平分线。
几何语言
∵AD是 △ ABC的角平分线(已知)
A
B
C
D
●
●
︶
︶
1
2
∴
(角平分线的定义)
2、三角形的角平分线的定义
锐角三角形的三条高交于三角形______一点.
直角三角形的三条高交于________.
锐角三角形的三条高不交于一点,三条高所在直线交于三角形______一点.
二、探究活动
内部
直角顶点
外部
A
B
C
D
E
F
A
B
C
D
O
A
B
C
D
E
F
活动1:三角形的三条高
分别指出图中△ABC 的三条高。
AB
CB
A
B
C
D
E
F
A
B
C
D
BD
CE
AD
直角边BC边上的
高是 ;
直角边AB边上的
高是 ;
斜边AC边上的
高是 ;
AB边上的高是 ;
BC边上的高是 ;
CA边上的高是 ;
BF
活动1:三角形的三条高
E
观察下列三个图形你有什么发现?
三角形的三条中线交于三角形_______一点.
A
C
B
●
●
D
E
F
●
●
●
●
●
●
●
D
D
F
E
三角形的三条中线的交点叫做三角形的_______.
A
A
B
B
F
C
C
●
●
●
●
●
●
●
●
●
●
●
●
活动2:三角形的中线
内部
重心
如图1-15,在△ABC中,AE是它的中线,AD是它的高线,则△ABE的面积与△AEC的面积的大小有怎样的关系?
A
B
D
E
C
三角形的中线把三角形分成两个面积相等的三角形。
解∵AE是BC边上的中线(已知)
∴ BE = EC(三角形中线的定义)
∴
∵
三角形中线性质:
活动2:三角形的中线
中线的性质
三角形的中线把三角形分成两个面积相等的三角形。
∵AE是BC边上的中线(已知)
∴
几何语言
活动2:三角形的中线
A
B
E
C
观察下列三个图形你有什么发现?
三角形的三条角平分线在三角形的_____交于一点
●
D
F
A
B
A
C
A
C
B
D
●
●
F
E
●
●
●
●
●
E
●
D
E
B
F
C
●
●
●
●
●
●
●
●
●
●
●
●
活动3:三角形的角平分线
内部
拓展练习
达标检测
2、三角形的下列线段中,能将三角形的面积分成相等的两部分的是( )
A.中线 B.角平分线
C.高 D. 以上答案均正确
1、下列各组图形中,哪一组图形中AD是△ABC 的高( )
A
D
C
B
A
B
C
D
A
B
C
D
A
B
C
D
(A)
(B)
(C)
(D)
D
A
达标检测
3、图中共有 个三角形,若BC=CD=DE,
则AC,AD分别是______ ,____的中线.
A
B
E
D
C
6
△ABD
△ACE
4、如图,在ΔABC中,AE是中线,AD是角平分线,AF是高。填空:
(1)BE= = ;
(2)∠BAD= = ;
(3)∠AFB= =90°;
(4)SΔABC= 。
CE
BC
∠CAD
∠BAC
∠AFC
BC?AF
达标检测
拓展提升
1、如图所示,已知AD是△ABC的边BC上的中线.
(1)作出△ABD的边BD上的高.
(2)若△ABC的面积为10,求△ADC的面积.
(3)若△ABD的面积为6,且BD边上的高为3,求BC的长.
A
B
C
D
解:(1)如图所示:
E
A
B
C
D
E
(2)∵AD是△ABC的边BC上的
∴△ADC的面积
= △ABC的面积=5.
中线,△ABC的面积为10,
(3)∵AD是△ABC的边BC上的
∴△ABC的面积为12,
∵BD边上的高为3,
∴BC=12×2÷3=8
中线,△ABD的面积为6,
(2)若△ABC的面积为10,求△ADC的面积.
(3)若△ABD的面积为6,且BD边上的高为3,求BC的长.
三角形的
重要线段
概念
图形
表示法
三角形
的高线
从三角形的一个顶点向它的对边所在的直线作垂线,顶点和垂足之间的线段
∵AD是△ABC的BC上的高线.
∴AD⊥BC
∠ADB=∠ADC=90°.
三角形
的中线
三角形中,连结一个顶点和它对边中的
线段
∵ AD是△ABC的BC上的中线.
∴ BD=CD= ?BC.
三角形的
角平分线
三角形一个内角的平分线与它的对边相交,这个角顶点与交点之间的线段
∵.AD是△ABC的∠BAC的平分线
∴ ∠1=∠2= ? ∠BAC
小结
今天你学习了什么?
向着目标
作业
课本P5 第2题
完成《数学基础训练》的基础达标
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
