浙教版初中数学七年级上册4.5 合并同类项 课件(25张)
文档属性
| 名称 | 浙教版初中数学七年级上册4.5 合并同类项 课件(25张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-21 10:26:20 | ||
图片预览








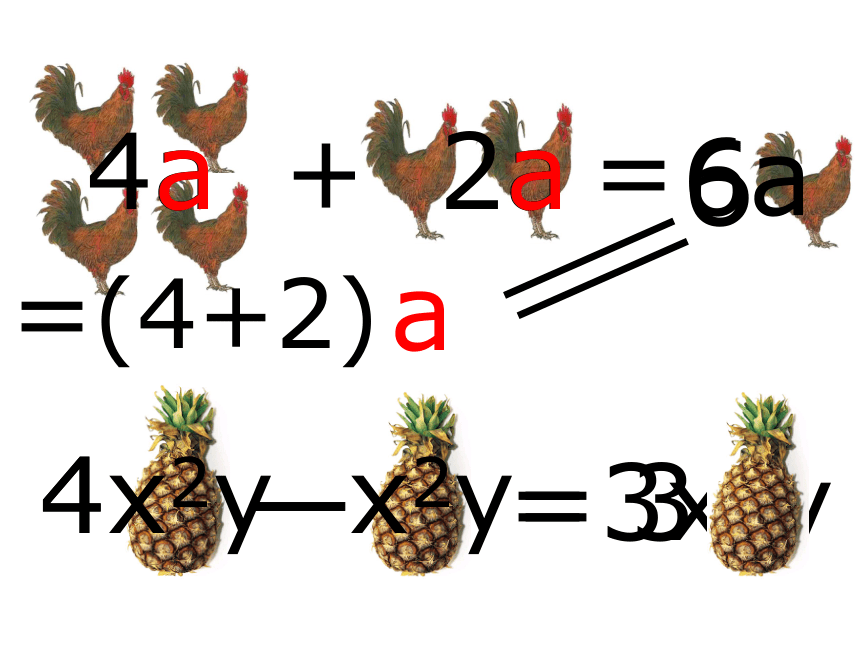
文档简介
(共24张PPT)
老师家里有一个储蓄罐,里面是老师平时存下来的硬币,现在想知道里面有多少钱?你能帮老师个忙吗?
为了快速的算出多少钱,你的第一步工作是怎么做的?
你是按照什么来分类的呢?
按照面值来分
看一看,把它们分分类;
说一说,你这样分的理由。
8m
12m
找一找,它们有什么共同的特点:
,
,
,
,
8m
12m
,
,
,
所含字母相同
相同字母的指数也相同
同类项
判断下列各组是不是同类项,为什么?
(1)x和y (2)a2b与ab2
(3)-3pq与3qp (4)bc与ac
(5)a2与a3
×
×
√
×
×
×
√
√
★与字母顺序无关;
★与系数无关!
多项式中,所含字母相同,并且相同字母的指数也相同的项,叫做同类项。
所有的常数项是同类项。
2x2y-2a2bc-5+x2y+3a2bc+2007
记住口诀
我们在生活中对事物进行分类可以带来方便,那数学中分类会有什么好处呢?
+ =
6
―
4a 2a
6a
=3x2y
a
a
= a
(4+2)
4
= 3
4x2y x2y
x2y
这样的过程叫做合并同类项.
把同类项的系数相加,所得的结果作为系数,
字母和字母的指数不变。
8
+
2
=
10
x2y
x2y
相加
不变
多项式中的同类项可以合并成一项,
8
+
2
10
=
法则
x2y
8
+
x2y
2
议一议:
这项法则其实是根据我们学过的哪一条运算律得到的?
(8+2)
x2y
=
x2y
10
=
一变一不变
一变就是系数要变
(新系数变为原来各系数的代数和)
一不变就是字母和字母的指数不变
(原来的字母和字母的指数照抄)
合并同类项:
(1)
(2)
;
;
(3)
;
瘦身俱乐部
(4)
;
不是同类项不可以合并
-3a2b与5b2a能不能合并?
判断
(1)5m-2m=3
(2)ab+2ab=3a2b2
(3)3x+2y=5xy
(4)-6x2+x2+5x2=0
×
×
×
√
=( )+( )
(1) 6xy-10x2-5yx+7x2
合并同类项
+5x
(找)
6xy-5yx
-10x2+7x2
(移)
= xy
(6-5)
+ x2
(-10+7)
(并)
=xy-3x2
+5x
+5x
+5x
练习:
(1) 3x-8x-9x
(2) 5a2+2ab-4a2-4ab
(3) 2x-7y-5x+11y-1
=-14x
=a2-2ab
=-3x+4y-1
例.已知a= ,b=4,求多项式
的值。
找
移
并
找准、找全同类项
连同前面的符号一起移,没有同类项的照抄
只把系数来相加,字母及字母指数不变
2a2b
-3a
-3a2b
+2a-4
☆怎样才能算得更快呢?
利用合并同类项给多项式减肥,能使运算更简便!
★同类项与系数无关,与字母顺序无关.
(2)并同类项的法则:
______________相加,作为结果的系数,字母和字母的指数______。
同类项的系数
不变
步骤:一找,二移,三合并.
2.所含的字母相同
3.相同字母的指数也相同
同类项的特点
1.都是单项式
(1)
课堂小结
⑵ -3x2y3 与2x2____
⑶ 2m___ 与 -5n2____
⑴ -3a____与 6b___
做一做:
请你在下面的横线上填上适当的内容,使两个单项式构成同类项。
b
a
n2
m
y3
如图,原立方体的体积为27a3,切去一部分后,剩下部分的体积为多少?
21a3
6+m=4
n+1=5
解得:
m=-2
n=4
1.3x+y-6y+ax合并同类项后不含x项.求a
数学日记
姓名 日期 .
今天数学课的课题: ;
今天涉及的重要数学知识: ;
理解最好的地方: ;
不明白或还需要进一步理解的地方: ;
独立(或需要帮助)完成探索活动并发现结论: ;
解决问题能否用不同的方法(具体指明有几个问题): ;
老师家里有一个储蓄罐,里面是老师平时存下来的硬币,现在想知道里面有多少钱?你能帮老师个忙吗?
为了快速的算出多少钱,你的第一步工作是怎么做的?
你是按照什么来分类的呢?
按照面值来分
看一看,把它们分分类;
说一说,你这样分的理由。
8m
12m
找一找,它们有什么共同的特点:
,
,
,
,
8m
12m
,
,
,
所含字母相同
相同字母的指数也相同
同类项
判断下列各组是不是同类项,为什么?
(1)x和y (2)a2b与ab2
(3)-3pq与3qp (4)bc与ac
(5)a2与a3
×
×
√
×
×
×
√
√
★与字母顺序无关;
★与系数无关!
多项式中,所含字母相同,并且相同字母的指数也相同的项,叫做同类项。
所有的常数项是同类项。
2x2y-2a2bc-5+x2y+3a2bc+2007
记住口诀
我们在生活中对事物进行分类可以带来方便,那数学中分类会有什么好处呢?
+ =
6
―
4a 2a
6a
=3x2y
a
a
= a
(4+2)
4
= 3
4x2y x2y
x2y
这样的过程叫做合并同类项.
把同类项的系数相加,所得的结果作为系数,
字母和字母的指数不变。
8
+
2
=
10
x2y
x2y
相加
不变
多项式中的同类项可以合并成一项,
8
+
2
10
=
法则
x2y
8
+
x2y
2
议一议:
这项法则其实是根据我们学过的哪一条运算律得到的?
(8+2)
x2y
=
x2y
10
=
一变一不变
一变就是系数要变
(新系数变为原来各系数的代数和)
一不变就是字母和字母的指数不变
(原来的字母和字母的指数照抄)
合并同类项:
(1)
(2)
;
;
(3)
;
瘦身俱乐部
(4)
;
不是同类项不可以合并
-3a2b与5b2a能不能合并?
判断
(1)5m-2m=3
(2)ab+2ab=3a2b2
(3)3x+2y=5xy
(4)-6x2+x2+5x2=0
×
×
×
√
=( )+( )
(1) 6xy-10x2-5yx+7x2
合并同类项
+5x
(找)
6xy-5yx
-10x2+7x2
(移)
= xy
(6-5)
+ x2
(-10+7)
(并)
=xy-3x2
+5x
+5x
+5x
练习:
(1) 3x-8x-9x
(2) 5a2+2ab-4a2-4ab
(3) 2x-7y-5x+11y-1
=-14x
=a2-2ab
=-3x+4y-1
例.已知a= ,b=4,求多项式
的值。
找
移
并
找准、找全同类项
连同前面的符号一起移,没有同类项的照抄
只把系数来相加,字母及字母指数不变
2a2b
-3a
-3a2b
+2a-4
☆怎样才能算得更快呢?
利用合并同类项给多项式减肥,能使运算更简便!
★同类项与系数无关,与字母顺序无关.
(2)并同类项的法则:
______________相加,作为结果的系数,字母和字母的指数______。
同类项的系数
不变
步骤:一找,二移,三合并.
2.所含的字母相同
3.相同字母的指数也相同
同类项的特点
1.都是单项式
(1)
课堂小结
⑵ -3x2y3 与2x2____
⑶ 2m___ 与 -5n2____
⑴ -3a____与 6b___
做一做:
请你在下面的横线上填上适当的内容,使两个单项式构成同类项。
b
a
n2
m
y3
如图,原立方体的体积为27a3,切去一部分后,剩下部分的体积为多少?
21a3
6+m=4
n+1=5
解得:
m=-2
n=4
1.3x+y-6y+ax合并同类项后不含x项.求a
数学日记
姓名 日期 .
今天数学课的课题: ;
今天涉及的重要数学知识: ;
理解最好的地方: ;
不明白或还需要进一步理解的地方: ;
独立(或需要帮助)完成探索活动并发现结论: ;
解决问题能否用不同的方法(具体指明有几个问题): ;
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
