1.3 解直角三角形(1)
图片预览


文档简介
(共19张PPT)
1.3解直角三角(1)
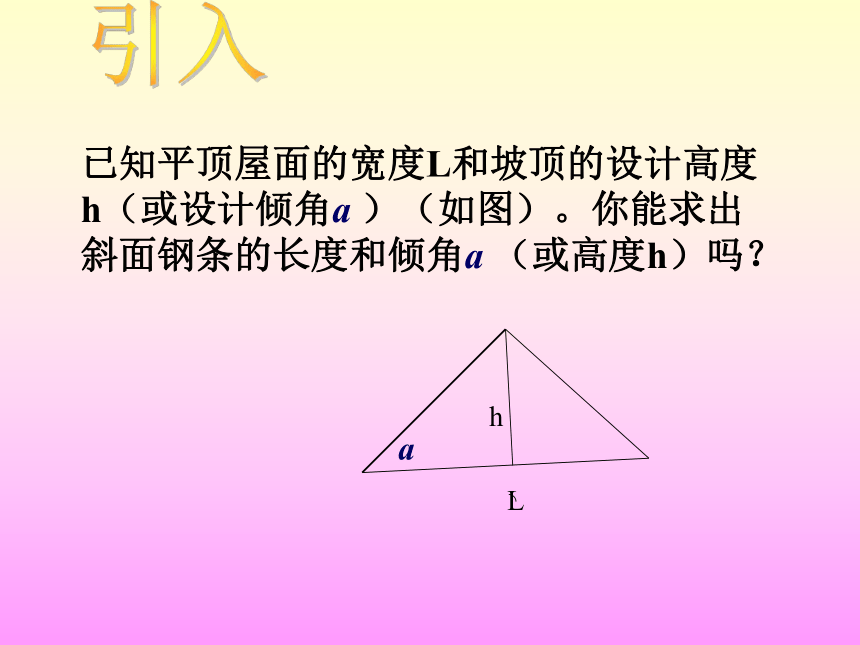
已知平顶屋面的宽度L和坡顶的设计高度h(或设计倾角a )(如图)。你能求出斜面钢条的长度和倾角a (或高度h)吗?
h
L
a
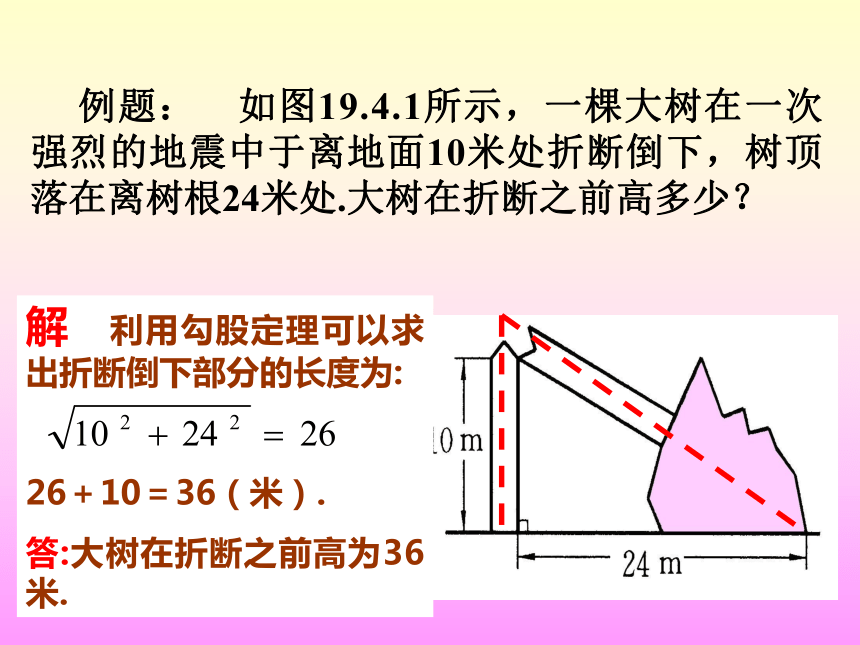
例题: 如图19.4.1所示,一棵大树在一次强烈的地震中于离地面10米处折断倒下,树顶落在离树根24米处.大树在折断之前高多少?
解 利用勾股定理可以求出折断倒下部分的长度为:
26+10=36(米).
答:大树在折断之前高为36米.
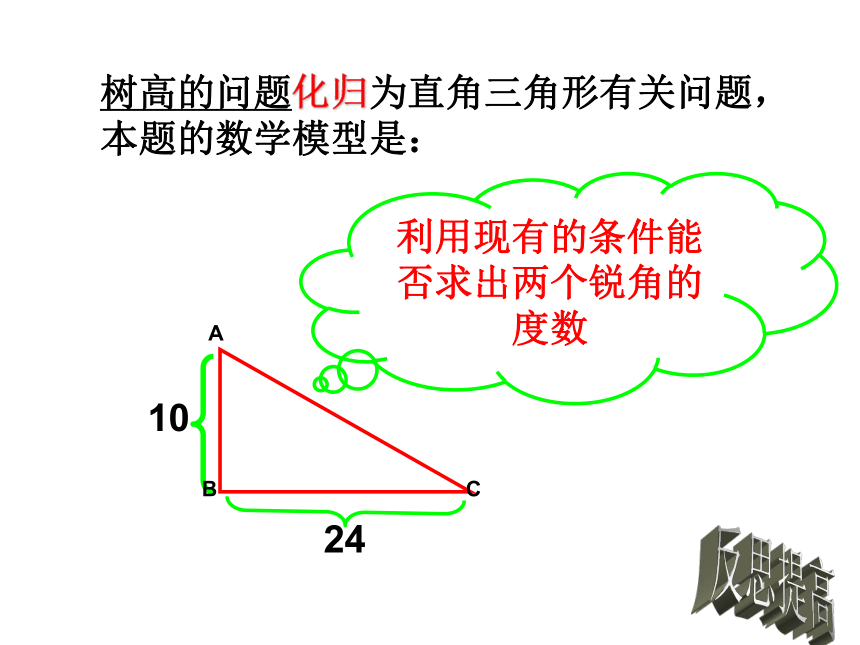
树高的问题化归为直角三角形有关问题,本题的数学模型是:
10
A
B
C
24
利用现有的条件能否求出两个锐角的度数
在例题中,我们还可以利用直角三角形的边角之间的关系求出另外两个锐角.像这样,
********************************
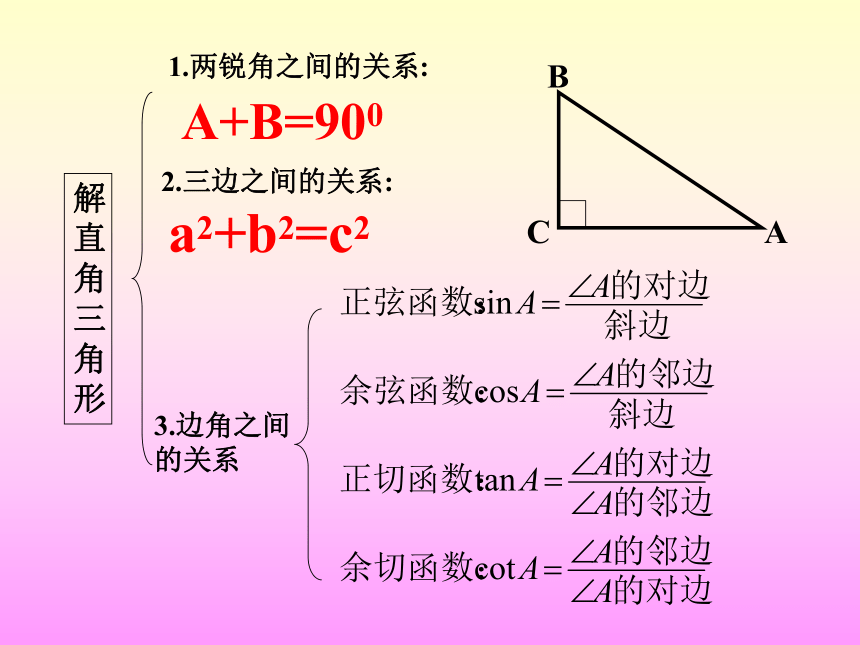
在直角三角形中,由已知的一些边、角,求出另一些边、角的过程,叫做解直角三角形.
解直角三角形
1.两锐角之间的关系:
2.三边之间的关系:
3.边角之间的关系
A+B=900
a2+b2=c2
C
A
B
在直角三角形中共有五个元素
线段
、
;
、
锐角
、
。
是不是已知其中两个都解直角三角形呢
解直角三角形,只有下面两种情况:
(1)已知两条边;
(2)已知一条边和一个锐角
C
A
B
例1:如图,在Rt△ABC中,∠C=90° ∠A=50°,AB=3。
求∠B和a,b
(sin50°=0.7660,cos 50 °=0.6428,
tan 50 °=1.1918,边长保留2个有效数字)
3
A
B
C
a
b
课内练习:p16
第一、二两大题
例2。(引入题中)已知平顶屋面的宽度L为10m,坡顶的设计高度h为3.5m,你能求出斜面钢条的长度和倾角a。
(tan34.9920°≈0.7, tan55.0080°≈10/7)
a
L
h
a
练习。 如图东西两炮台A、B相距2000米,同时发现入侵敌舰C,炮台A测得敌舰C在它的南偏东40゜的方向,炮台B测得敌舰C在它的正南方,试求敌舰与两炮台的距离.(精确到1米, sin40°≈0.6428, cos40°≈0.7660, tan40°≈0.8391
sin50°≈0.7660, cos50°≈0.6428, tan50°≈1.1918)
本题是已知一边,一锐角.
解 在Rt△ABC中,因为
∠CAB=90゜-∠DAC=50゜,
=tan∠CAB,
所以 BC=AB tan∠CAB
=2000×tan50゜
≈2384(米).
又因为 ,
所以
AC=
答:敌舰与A、B两炮台的距离分别约为3111米和2384米.
在⊿ABC中,∠C=900,
解直角三角形:(如图)
C
A
B
1.已知a,b.解直角三角形(即求:∠A,∠B及C边)
2. 已知∠A,a.解直角三角形
3.已知∠A,b. 解直角三角形
4. 已知∠A,c. 解直角三角形
这节课你有哪些收获
1.3解直角三角(1)
已知平顶屋面的宽度L和坡顶的设计高度h(或设计倾角a )(如图)。你能求出斜面钢条的长度和倾角a (或高度h)吗?
h
L
a
例题: 如图19.4.1所示,一棵大树在一次强烈的地震中于离地面10米处折断倒下,树顶落在离树根24米处.大树在折断之前高多少?
解 利用勾股定理可以求出折断倒下部分的长度为:
26+10=36(米).
答:大树在折断之前高为36米.
树高的问题化归为直角三角形有关问题,本题的数学模型是:
10
A
B
C
24
利用现有的条件能否求出两个锐角的度数
在例题中,我们还可以利用直角三角形的边角之间的关系求出另外两个锐角.像这样,
********************************
在直角三角形中,由已知的一些边、角,求出另一些边、角的过程,叫做解直角三角形.
解直角三角形
1.两锐角之间的关系:
2.三边之间的关系:
3.边角之间的关系
A+B=900
a2+b2=c2
C
A
B
在直角三角形中共有五个元素
线段
、
;
、
锐角
、
。
是不是已知其中两个都解直角三角形呢
解直角三角形,只有下面两种情况:
(1)已知两条边;
(2)已知一条边和一个锐角
C
A
B
例1:如图,在Rt△ABC中,∠C=90° ∠A=50°,AB=3。
求∠B和a,b
(sin50°=0.7660,cos 50 °=0.6428,
tan 50 °=1.1918,边长保留2个有效数字)
3
A
B
C
a
b
课内练习:p16
第一、二两大题
例2。(引入题中)已知平顶屋面的宽度L为10m,坡顶的设计高度h为3.5m,你能求出斜面钢条的长度和倾角a。
(tan34.9920°≈0.7, tan55.0080°≈10/7)
a
L
h
a
练习。 如图东西两炮台A、B相距2000米,同时发现入侵敌舰C,炮台A测得敌舰C在它的南偏东40゜的方向,炮台B测得敌舰C在它的正南方,试求敌舰与两炮台的距离.(精确到1米, sin40°≈0.6428, cos40°≈0.7660, tan40°≈0.8391
sin50°≈0.7660, cos50°≈0.6428, tan50°≈1.1918)
本题是已知一边,一锐角.
解 在Rt△ABC中,因为
∠CAB=90゜-∠DAC=50゜,
=tan∠CAB,
所以 BC=AB tan∠CAB
=2000×tan50゜
≈2384(米).
又因为 ,
所以
AC=
答:敌舰与A、B两炮台的距离分别约为3111米和2384米.
在⊿ABC中,∠C=900,
解直角三角形:(如图)
C
A
B
1.已知a,b.解直角三角形(即求:∠A,∠B及C边)
2. 已知∠A,a.解直角三角形
3.已知∠A,b. 解直角三角形
4. 已知∠A,c. 解直角三角形
这节课你有哪些收获
