相似三角形复习课

(共14张PPT)
相似三角形复习（1）
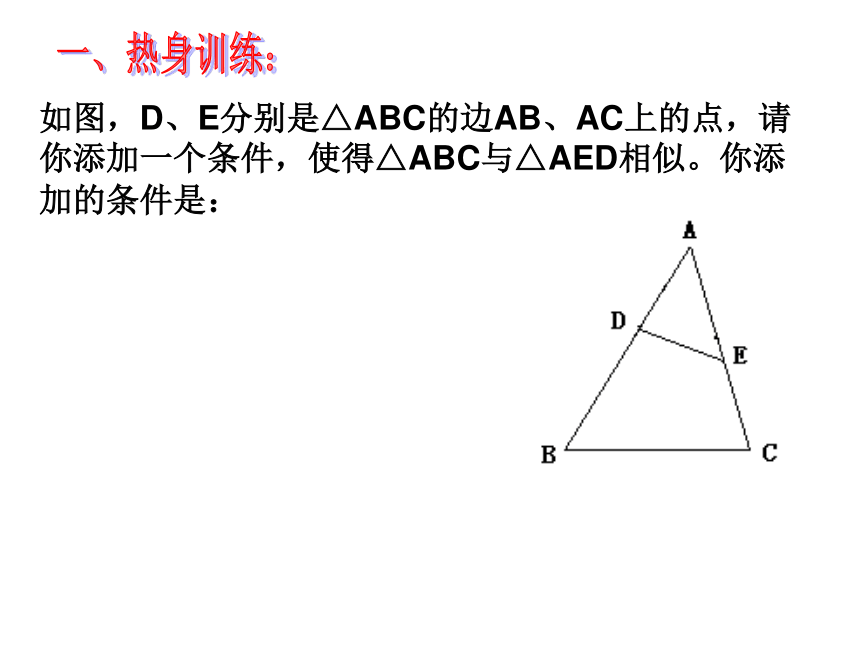
如图，D、E分别是△ABC的边AB、AC上的点，请你添加一个条件，使得△ABC与△AED相似。你添加的条件是：
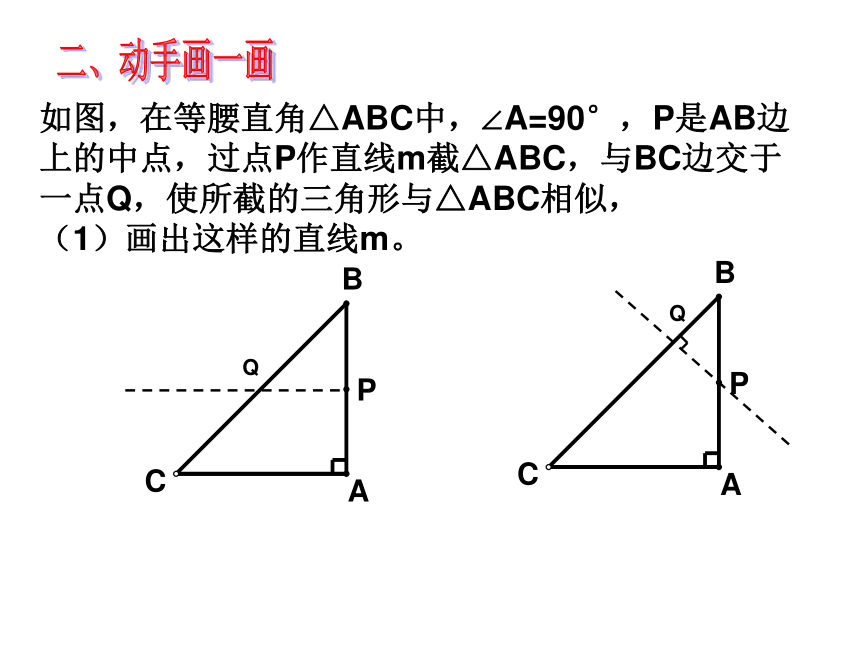
如图，在等腰直角△ABC中，∠A=90°，P是AB边上的中点，过点P作直线m截△ABC，与BC边交于一点Q，使所截的三角形与△ABC相似，
（1）画出这样的直线m。
Q
Q
Q
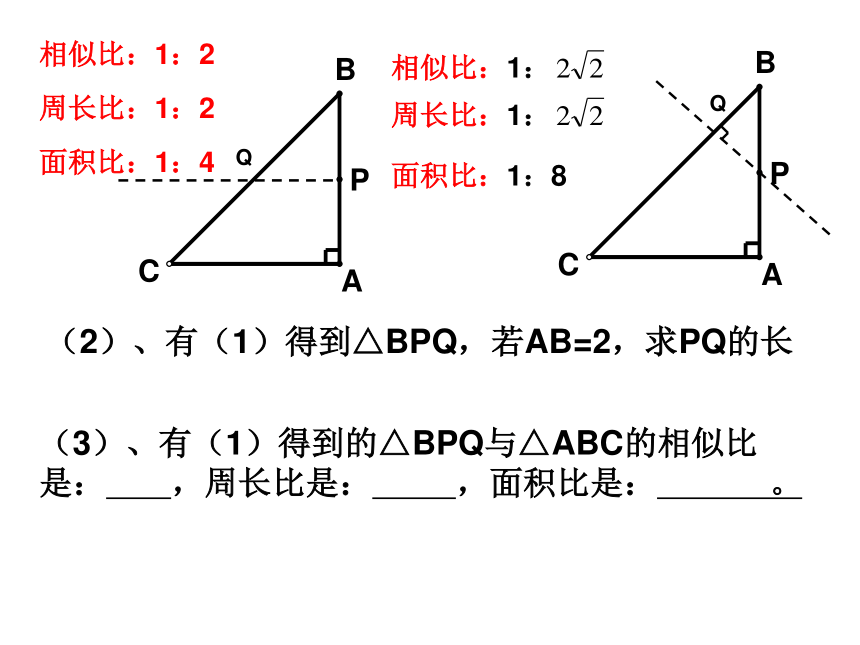
（2）、有（1）得到△BPQ，若AB=2，求PQ的长
（3）、有（1）得到的△BPQ与△ABC的相似比是： ，周长比是： ，面积比是： 。
相似比：1：2
周长比：1：2
面积比：1：4
面积比：1：8
相似比：1：
周长比：1：
Q
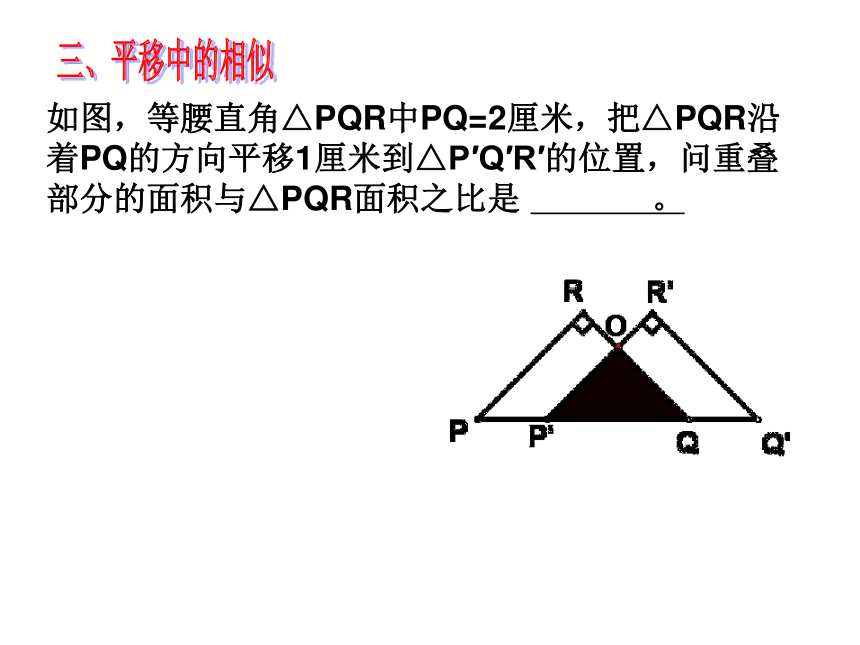
如图，等腰直角△PQR中PQ=2厘米，把△PQR沿着PQ的方向平移1厘米到△P′Q′R′的位置，问重叠部分的面积与△PQR面积之比是 。
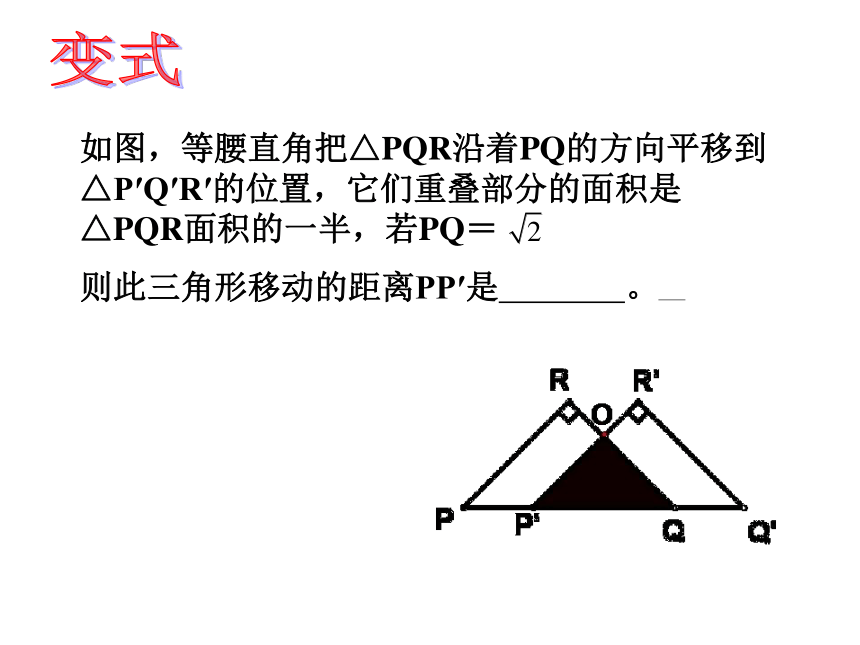
如图，等腰直角把△PQR沿着PQ的方向平移到△P′Q′R′的位置，它们重叠部分的面积是△PQR面积的一半，若PQ＝
则此三角形移动的距离PP′是 。
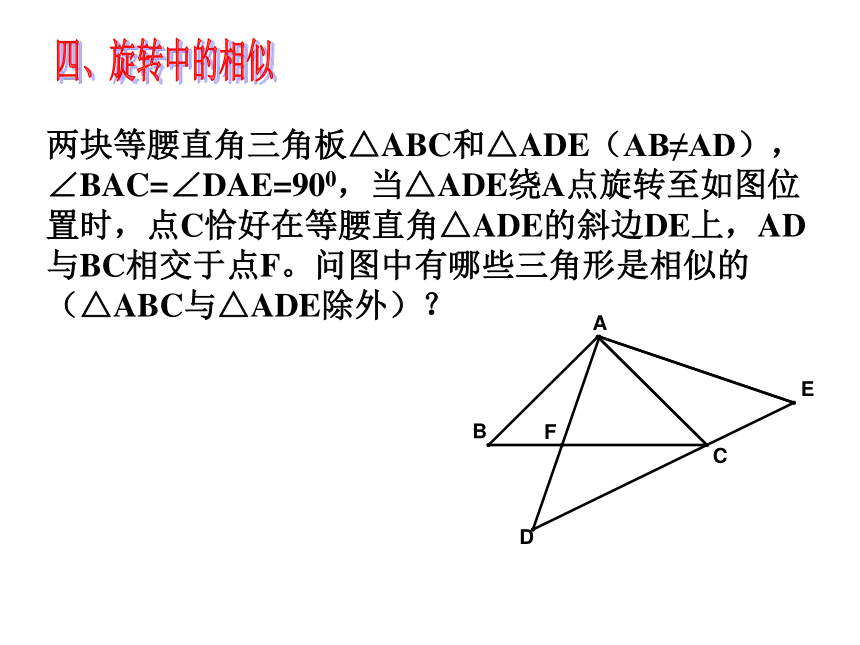
两块等腰直角三角板△ABC和△ADE（AB≠AD），∠BAC=∠DAE=900，当△ADE绕A点旋转至如图位置时，点C恰好在等腰直角△ADE的斜边DE上，AD与BC相交于点F。问图中有哪些三角形是相似的（△ABC与△ADE除外）？
在同一平面内,将两个全等的等腰直角三角形ABC和AFG摆放在一起，A为公共顶点，∠BAC=∠AFG=90°，它们的斜边长为2，若 ABC固定不动， AFG绕点A旋转，AF、AG与边BC的交点分别为D、E(点D不与点B重合,点E不与点C重合)。
图中有相似（不包括全等）三角形吗？如有，把它们一 一写出来.
在 △ABC中，AB=AC=2，∠A=90°，若将三角板45度角的顶点放在斜边BC的中点O处，一直角边经过点A，如图（1），三角板绕O点顺时针方向旋转，使两边与Rt△ABC的两边AB、AC分别相交于点E、F，如图（2），设BE=x，CF=y。
（1）试说明△BOE∽△CFO。
(2)求y与x的函数关系式。
1、相似三角形的判定方法有哪些？
（1）平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似；
（2）有两个角对应相等的两个三角形相似；
（3）两边对应成比例,且夹角相等的两个三角形相似；
（4）三边对应成比例的两个三角形相似.
2、相似三角形的性质有哪些？
1、相似三角形的对应角相等，对应边成比例。
2、相似三角形的周长比等于相似比，对应高的比等于相似比、面积比等于相似比的平方
赵亮同学想利用影长测量学校旗杆的高度，如图，他在某一时刻立1米长的标杆测得其影长为1.2米，同时旗杆的投影一部分在地面上，另一部分在某一建筑的墙上，分别测得其长度为9.6米和2米，则学校旗杆的高度为 米．
9.6米
2米
小明想利用太阳光测量楼高，他带着皮尺来到一栋楼下，发现对面墙上有这栋楼的影子，针对这种情况，他设计了一种测量方案，具体测量情况如下：如示意图，小明边移动边观察，发现站到点E处时，可以使自己落在墙上的影子与这栋楼落在墙上的影子重叠，且高度恰好相同．此时，测得小明落在墙上的影子高度CD＝1.2m，CE＝0.8m，CA＝30m（点A、E、C在同一直线上）．已知小明的身高EF是1.7m，请你帮小明求出楼高AB（结果精确到0.1m）．