5.1多边形（3）

(共25张PPT)
玩游戏要适可而止，
千万不能影响学业哦！
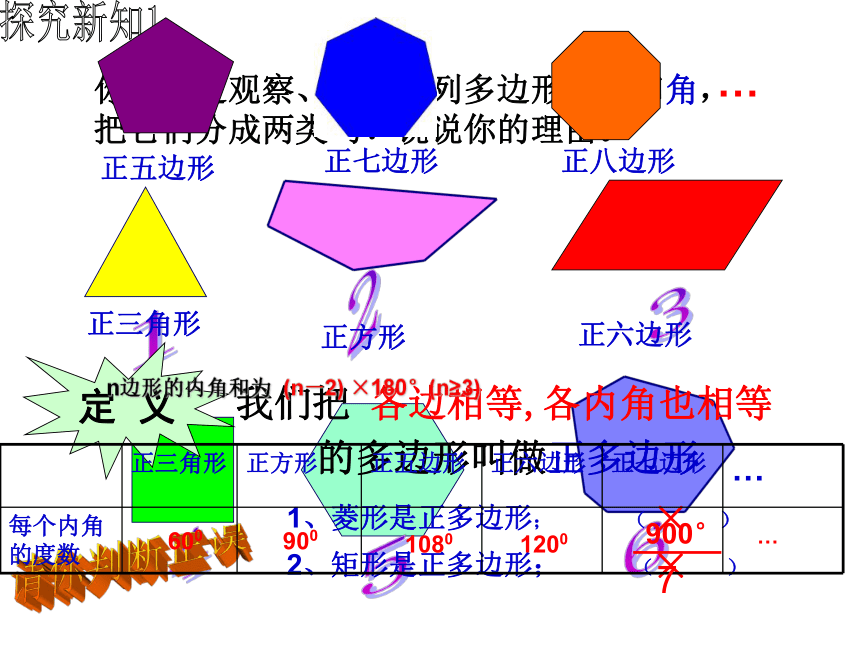
你能通过观察、分析下列多边形的边和角，把它们分成两类吗？说说你的理由。
各边相等,各内角也相等
定 义
我们把
的多边形叫做正多边形
正方形
正三角形
正六边形
正五边形
正七边形
正八边形
1、菱形是正多边形； （ ）
2、矩形是正多边形； （ ）
×
×
…
n边形的内角和为
(n－2) ×180°(n≥3)
正三角形 正方形 正五边形 正六边形 正七边形 …
每个内角的度数
1080
1200
…
900°
7
900
600
…
正五边形
正七边形
正八边形
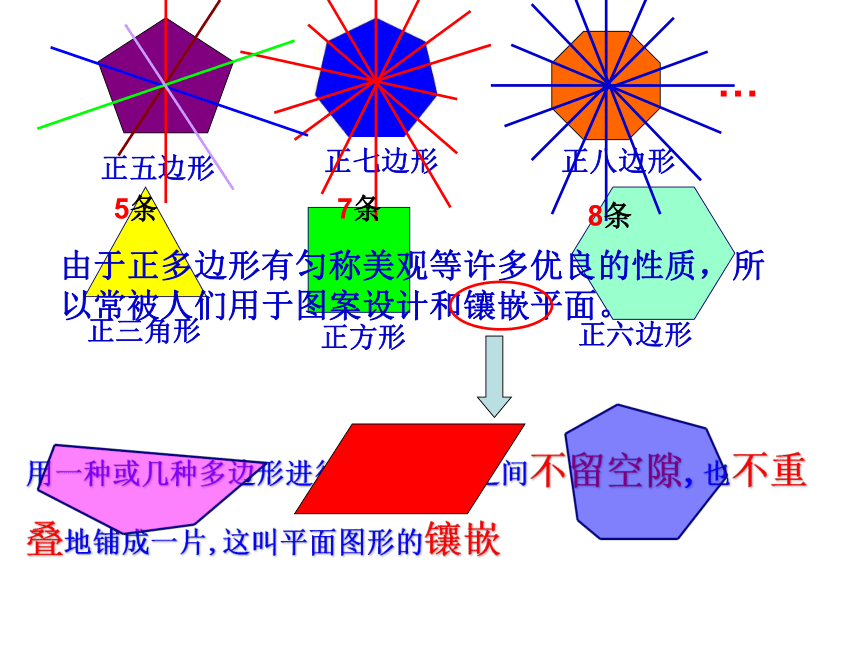
5条
8条
7条
正方形
正三角形
正六边形
由于正多边形有匀称美观等许多优良的性质，所以常被人们用于图案设计和镶嵌平面。
用一种或几种多边形进行拼接,彼此之间不留空隙,也不重叠地铺成一片,这叫平面图形的镶嵌
分别用若干个正三角形、正方形、正五边形、正六边形的纸片尝试镶嵌平面，你发现这几种正多边形哪些能单独镶嵌平面，哪些不能？你能说明其中的原因吗？
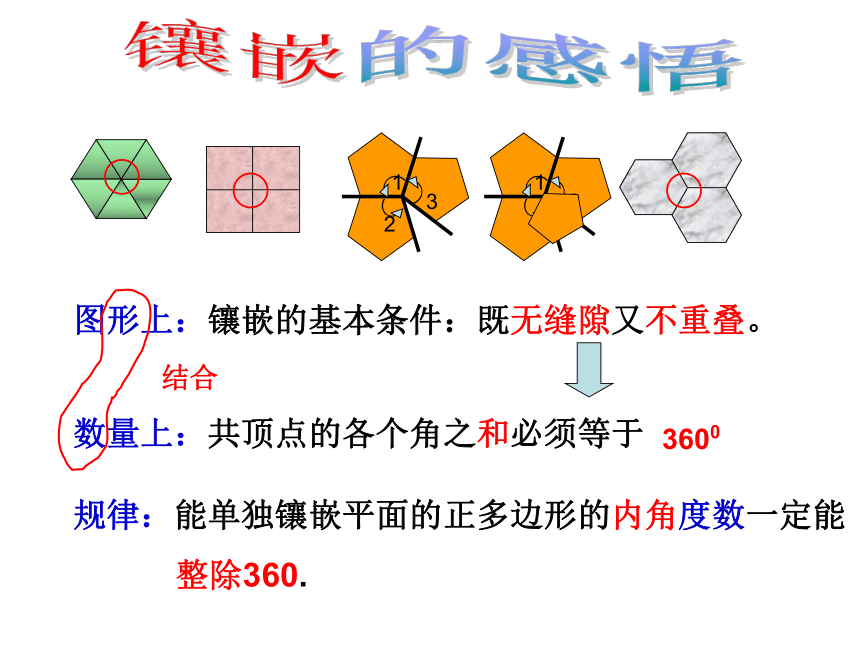
注意了：镶嵌时要做到既无缝隙又不重叠。
图形上：镶嵌的基本条件：既无缝隙又不重叠。
数量上：共顶点的各个角之和必须等于
1
2
3
1
3
规律：能单独镶嵌平面的正多边形的内角度数一定能
整除360.
3600
结合
1
2
3
1
3
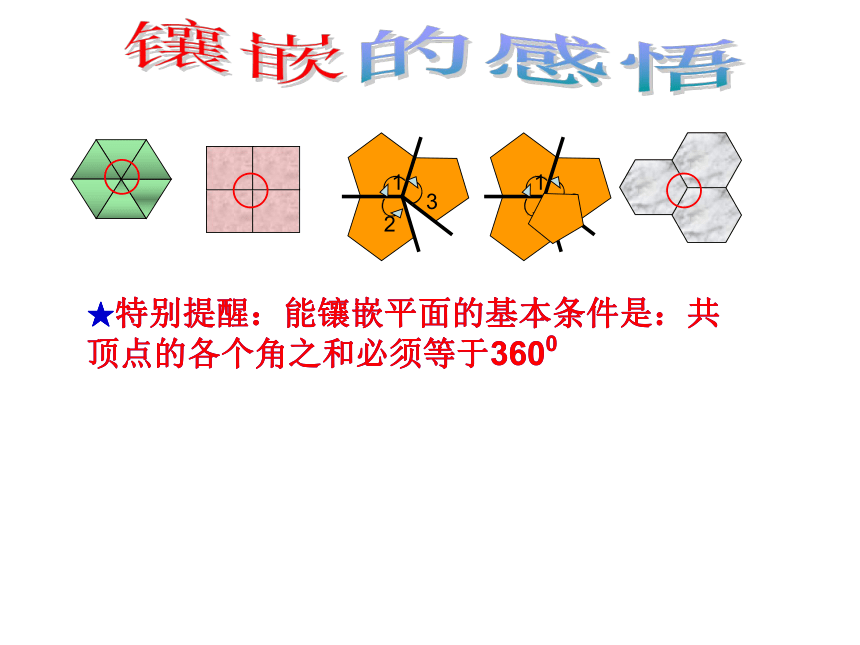
★特别提醒：能镶嵌平面的基本条件是：共顶点的各个角之和必须等于3600
★特别提醒：能镶嵌平面的基本条件是：共顶点的各个角之和必须等于3600
根据以上镶嵌的基本条件，你能说说全等的三角形能单独镶嵌平面数学原理吗？
根据以上镶嵌的基本条件，你能说说全等的四边形能单独镶嵌平面数学原理吗？
2
4
1
3
2
4
1
3
2
4
1
3
2
4
1
3
2
4
1
3
我们知道：能镶嵌平面的基本条件是：拼接在同一个点的各个角的和等于360° 。
用边长相等的正三角形和正方形能镶嵌平面吗？ 如果能，画出镶嵌的示意图，并说说它们能镶嵌平面的数学原理。
正三角形
正方形
解：能，因为正三角形的内角为60°，正方形的内角为90°,由于60×3+90×2＝360，所以两个正八边形和一个正方形能拼成一幅镶嵌图.
我们知道：能镶嵌平面的基本条件是：拼接在同一个点的各个角的和等于360° 。
用边长相等的正三角形和正方形能镶嵌平面吗？
正八边形
正方形
我们知道：能镶嵌平面的基本条件是：拼接在同一个点的各个角的和等于360° 。
用边长相等的正八边形和正方形能镶嵌平面吗 如 能，说出它们能镶嵌平面的数学原理。
我们知道：能镶嵌平面的关键是：拼接在同一个点的各个角的和等于360° 。
用边长相等的正八边形和正方形能镶嵌平面吗？
课 堂 小 结
通过本节课的学习，你学到了什么？有什么收获呢？让我们一起回顾与分享吧！
1、能单独镶嵌平面的正多边形只有三种：
正三角形、正方形、正六边形
规律：正多边形的内角度数一定是360的约数；
2、多种正多边形能镶嵌平面的基本条件:
共顶点的各个角之和为3600.
用边长相等的正三角形和正方形能镶嵌平面
多种正边形镶嵌平面.
必做题：1、P100 做一做 ：2
2、 P101 A组：1、2、3
选做题：1、P101 B组、C组
2、请你用两种或两种以上的多边形设计镶嵌图案，画出示意图并说明它的意义，如：