浙教版九年级上册 第四章《相似三角形》单元练习(word版含解析)
文档属性
| 名称 | 浙教版九年级上册 第四章《相似三角形》单元练习(word版含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-23 00:00:00 | ||
图片预览

文档简介
九上第四章《相似三角形》单元练习(实验中学)
【巩固练习】
1.已知=,则的值是(
)
A.
B.
C.
D.
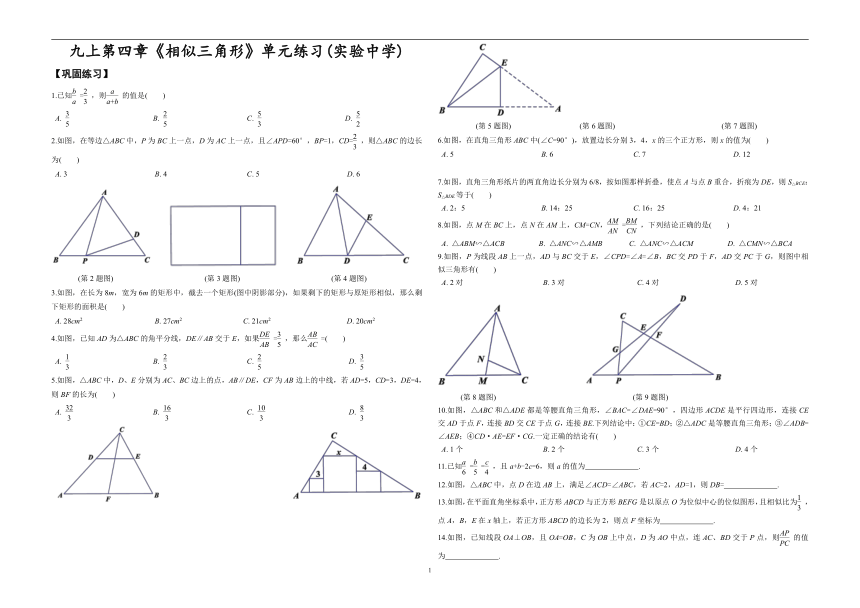
2.如图,在等边△ABC中,P为BC上一点,D为AC上一点,且∠APD=60°,BP=1,CD=,则△ABC的边长为(
)
A.
3
B.
4
C.
5
D.
6
(第2题图)
(第3题图)
(第4题图)
3.如图,在长为8m,宽为6m的矩形中,截去一个矩形(图中阴影部分),如果剩下的矩形与原矩形相似,那么剩下矩形的面积是(
)
A.
28cm2
B.
27cm2
C.
21cm2
D.
20cm2
4.如图,已知AD为△ABC的角平分线,DE∥AB交于E,如果=,那么=(
)
A.
B.
C.
D.
5.如图,△ABC中,D、E分别为AC、BC边上的点,AB∥DE,CF为AB边上的中线,若AD=5,CD=3,DE=4,则BF的长为(
)
A.
B.
C.
D.
(第5题图)
(第6题图)
(第7题图)
6.如图,在直角三角形ABC中(∠C=90°),放置边长分别3,4,x的三个正方形,则x的值为(
)
A.
5
B.
6
C.
7
D.
12
7.如图,直角三角形纸片的两直角边长分别为6/8,按如图那样折叠,使点A与点B重合,折痕为DE,则S△BCE:S△BDE等于(
)
A.
2:5
B.
14:25
C.
16:25
D.
4:21
8.如图,点M在BC上,点N在AM上,CM=CN,=,下列结论正确的是(
)
A.
△ABM∽△ACB
B.
△ANC∽△AMB
C.
△ANC∽△ACM
D.
△CMN∽△BCA
9.如图,P为线段AB上一点,AD与BC交于E,∠CPD=∠A=∠B,BC交PD于F,AD交PC于G,则图中相似三角形有(
)
A.
2对
B.
3对
C.
4对
D.
5对
(第8题图)
(第9题图)
10.如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,四边形ACDE是平行四边形,连接CE交AD于点F,连接BD交CE于点G,连接BE.下列结论中:①CE=BD;②△ADC是等腰直角三角形;③∠ADB=∠AEB;④CD·AE=EF·CG.一定正确的结论有(
)
A.
1个
B.
2个
C.
3个
D.
4个
11.已知==,且a+b-2c=6,则a的值为
.
12.如图,△ABC中,点D在边AB上,满足∠ACD=∠ABC,若AC=2,AD=1,则DB=
.
13.如图,在平面直角坐标系中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为,点A,B,E在x轴上,若正方形ABCD的边长为2,则点F坐标为
.
14.如图,已知线段OA⊥OB,且OA=OB,C为OB上中点,D为AO中点,连AC、BD交于P点,则的值为
.
(第10题图)
(第12题图)
(第13题图)
15.如图,正方形ABCD的边长为2,E,F分别为边AB,AD的中点,G是CF上的一点,且3CG=2GF,则△BEG的面积是
.
16.如果,在△ABC中,AB=AC,点E、F分别在AB和AC上,CE与BF相交于点D,若AE=CF,D为BF的中点,则=
.
(第14题图)
(第15题图)
(第16题图)
17.如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC;
(2)若AB=4,AD=3,AE=3,求AF的长.
18.如图,⊙O是△ABC的外接圆,AB=AC.求证:AB2=AE·AD.
19.如图,CD是Rt△ABC斜边上的高,E为AC的中点,ED交CB的延长线于F.求证:BD·CF=CD·DF.
20.如图,在△ABC中,AB=AC=5,BC=6,P是BC上的一个动点(与B、C不重合),PE⊥AB于点E,PF⊥BC交AC于点F,设PC=x,记PE=y1,PF=y2.
(1)分别求y1、y2关于x的函数关系式;
(2)△PEF能为直角三角形吗?若能,求出CP的长,若不能,请说明理由.
21.如图,已知抛物线与x轴交于A(2,0)、B(6,0)两点,与y轴交于C(0,3)点.
(1)求此抛物线的解析式;
(2)抛物线上有一点P,满足∠PBC=90°,求点P的坐标;
(3)在(2)的条件下,问在y轴上是否存在点E,使得以A、O、E为顶点的三角形与△PBC相似?若存在,求出点E的坐标;若不存在,请说明理由.
22.(1)如图1,在△ABC中,点D,E,Q分别在AB,AC,BC上,且DE∥BC,AQ交DE于点P,求证:=.
(2)如图2、3,在△ABC中,∠BAC=90°,正方形DEFG的四个顶点在△ABC的边上,连接AG,AF分别交DE于M,N两点.
①如图2,若AB=AC=1,则MN=
;
②如图3,求证:MN2=DM·EN.
【巩固练习】
1.已知=,则的值是(
)
A.
B.
C.
D.
2.如图,在等边△ABC中,P为BC上一点,D为AC上一点,且∠APD=60°,BP=1,CD=,则△ABC的边长为(
)
A.
3
B.
4
C.
5
D.
6
(第2题图)
(第3题图)
(第4题图)
3.如图,在长为8m,宽为6m的矩形中,截去一个矩形(图中阴影部分),如果剩下的矩形与原矩形相似,那么剩下矩形的面积是(
)
A.
28cm2
B.
27cm2
C.
21cm2
D.
20cm2
4.如图,已知AD为△ABC的角平分线,DE∥AB交于E,如果=,那么=(
)
A.
B.
C.
D.
5.如图,△ABC中,D、E分别为AC、BC边上的点,AB∥DE,CF为AB边上的中线,若AD=5,CD=3,DE=4,则BF的长为(
)
A.
B.
C.
D.
(第5题图)
(第6题图)
(第7题图)
6.如图,在直角三角形ABC中(∠C=90°),放置边长分别3,4,x的三个正方形,则x的值为(
)
A.
5
B.
6
C.
7
D.
12
7.如图,直角三角形纸片的两直角边长分别为6/8,按如图那样折叠,使点A与点B重合,折痕为DE,则S△BCE:S△BDE等于(
)
A.
2:5
B.
14:25
C.
16:25
D.
4:21
8.如图,点M在BC上,点N在AM上,CM=CN,=,下列结论正确的是(
)
A.
△ABM∽△ACB
B.
△ANC∽△AMB
C.
△ANC∽△ACM
D.
△CMN∽△BCA
9.如图,P为线段AB上一点,AD与BC交于E,∠CPD=∠A=∠B,BC交PD于F,AD交PC于G,则图中相似三角形有(
)
A.
2对
B.
3对
C.
4对
D.
5对
(第8题图)
(第9题图)
10.如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,四边形ACDE是平行四边形,连接CE交AD于点F,连接BD交CE于点G,连接BE.下列结论中:①CE=BD;②△ADC是等腰直角三角形;③∠ADB=∠AEB;④CD·AE=EF·CG.一定正确的结论有(
)
A.
1个
B.
2个
C.
3个
D.
4个
11.已知==,且a+b-2c=6,则a的值为
.
12.如图,△ABC中,点D在边AB上,满足∠ACD=∠ABC,若AC=2,AD=1,则DB=
.
13.如图,在平面直角坐标系中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为,点A,B,E在x轴上,若正方形ABCD的边长为2,则点F坐标为
.
14.如图,已知线段OA⊥OB,且OA=OB,C为OB上中点,D为AO中点,连AC、BD交于P点,则的值为
.
(第10题图)
(第12题图)
(第13题图)
15.如图,正方形ABCD的边长为2,E,F分别为边AB,AD的中点,G是CF上的一点,且3CG=2GF,则△BEG的面积是
.
16.如果,在△ABC中,AB=AC,点E、F分别在AB和AC上,CE与BF相交于点D,若AE=CF,D为BF的中点,则=
.
(第14题图)
(第15题图)
(第16题图)
17.如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC;
(2)若AB=4,AD=3,AE=3,求AF的长.
18.如图,⊙O是△ABC的外接圆,AB=AC.求证:AB2=AE·AD.
19.如图,CD是Rt△ABC斜边上的高,E为AC的中点,ED交CB的延长线于F.求证:BD·CF=CD·DF.
20.如图,在△ABC中,AB=AC=5,BC=6,P是BC上的一个动点(与B、C不重合),PE⊥AB于点E,PF⊥BC交AC于点F,设PC=x,记PE=y1,PF=y2.
(1)分别求y1、y2关于x的函数关系式;
(2)△PEF能为直角三角形吗?若能,求出CP的长,若不能,请说明理由.
21.如图,已知抛物线与x轴交于A(2,0)、B(6,0)两点,与y轴交于C(0,3)点.
(1)求此抛物线的解析式;
(2)抛物线上有一点P,满足∠PBC=90°,求点P的坐标;
(3)在(2)的条件下,问在y轴上是否存在点E,使得以A、O、E为顶点的三角形与△PBC相似?若存在,求出点E的坐标;若不存在,请说明理由.
22.(1)如图1,在△ABC中,点D,E,Q分别在AB,AC,BC上,且DE∥BC,AQ交DE于点P,求证:=.
(2)如图2、3,在△ABC中,∠BAC=90°,正方形DEFG的四个顶点在△ABC的边上,连接AG,AF分别交DE于M,N两点.
①如图2,若AB=AC=1,则MN=
;
②如图3,求证:MN2=DM·EN.
同课章节目录
