华东师大版九年级下册数学:26.2.2二次函数y=a(x-h)2+k的图象与性质 学案
文档属性
| 名称 | 华东师大版九年级下册数学:26.2.2二次函数y=a(x-h)2+k的图象与性质 学案 | 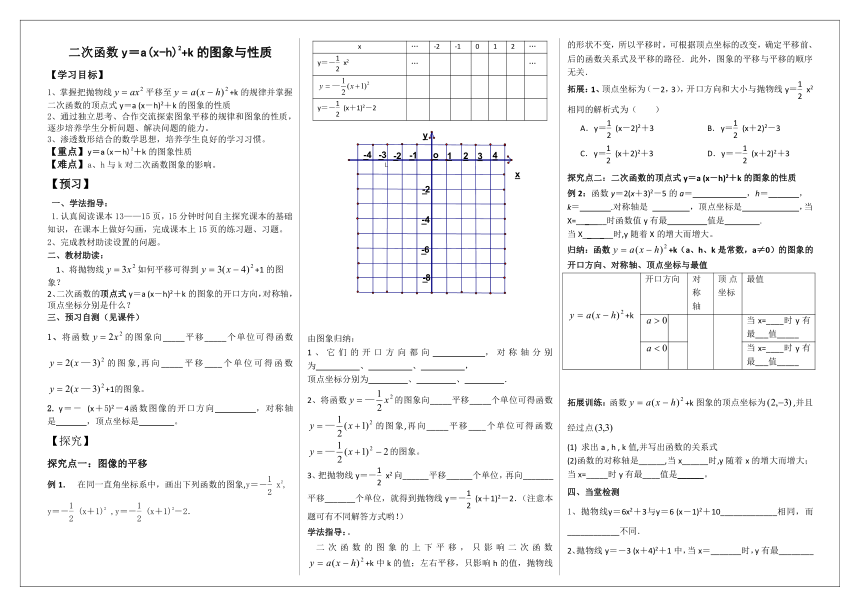 | |
| 格式 | zip | ||
| 文件大小 | 144.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-24 13:27:48 | ||
图片预览

文档简介
二次函数y=a(x-h)2+k的图象与性质
【学习目标】
1、掌握把抛物线平移至+k的规律并掌握二次函数的顶点式y=a
(x-h)2+k的图象的性质
2、通过独立思考、合作交流探索图象平移的规律和图象的性质,逐步培养学生分析问题、解决问题的能力。
3、渗透数形结合的数学思想,培养学生良好的学习习惯。
【重点】y=a(x-h)2+k的图象性质
【难点】a、h与k对二次函数图象的影响。
【预习】
一、学法指导:
1.认真阅读课本13——15页,15分钟时间自主探究课本的基础知识,在课本上做好勾画,完成课本上15页的练习题、习题。
2、完成教材助读设置的问题。
二、教材助读:
1、将抛物线如何平移可得到+1的图象?
2、二次函数的顶点式y=a
(x-h)2+k的图象的开口方向,对称轴,顶点坐标分别是什么?
三、预习自测(见课件)
1、将函数的图象向_____平移_____个单位可得函数的图象,再向_____平移____个单位可得函数+1的图象。
2.
y=-
(x+5)2-4函数图像的开口方向
,对称轴是
,顶点坐标是
。
【探究】
探究点一:图像的平移
在同一直角坐标系中,画出下列函数的图象,y=-x2,
y=-(x+1)2
,y=-(x+1)2-2.
x
…
-2
-1
0
1
2
…
y=-x2
…
…
y=-(x+1)2-2
由图象归纳:
1、它们的开口方向都向
,对称轴分别为
、
、
,
顶点坐标分别为
、
、
.
2、将函数的图象向_____平移_____个单位可得函数的图象,再向_____平移____个单位可得函数的图象。
3、把抛物线y=-x2向______平移______个单位,再向_______平移_______个单位,就得到抛物线y=-(x+1)2-2.(注意本题可有不同解答方式哟!)
学法指导:。
二次函数的图象的上下平移,只影响二次函数+k中k的值;左右平移,只影响h的值,抛物线的形状不变,所以平移时,可根据顶点坐标的改变,确定平移前、
后的函数关系式及平移的路径.此外,图象的平移与平移的顺序无关.
拓展:1、顶点坐标为(-2,3),开口方向和大小与抛物线y=x2相同的解析式为(
)
A.y=(x-2)2+3
B.y=(x+2)2-3
C.y=(x+2)2+3
D.y=-(x+2)2+3
探究点二:二次函数的顶点式y=a
(x-h)2+k的图象的性质
例2:函数y=2(x+3)2-5的a=
,h=
,
k=
.对称轴是
,顶点坐标是
,当X=___
__时函数值y有最
值是
.
当X__
___时,y随着X的增大而增大。
归纳:函数+k(a、h、k是常数,a≠0)的图象的开口方向、对称轴、顶点坐标与最值
+k
开口方向
对称轴
顶点坐标
最值
当x=____时y有最___值_____
当x=____时y有最___值_____
拓展训练:函数+k图象的顶点坐标为,并且经过点
(1)
求出a
,
h
,
k值,并写出函数的关系式
(2)函数的对称轴是______,当x______时,y随着x的增大而增大;当x=_____时y有最____值是______。
四、当堂检测
1、抛物线y=6x2+3与y=6
(x-1)2+10_____________相同,而____________不同.
2、抛物线y=-3
(x+4)2+1中,当x=_______时,y有最________值是________.
3、若抛物线y=a
(x-1)2+k上有一点A(3,5),则点A关于对称轴对称点A′的坐标为_____________.
五、训练
1、
y=3x2
y=-x2+1
y=(x+2)2
y=-4
(x-5)2-3
开口方向
顶点
对称轴
最值
增减性
(对称轴左侧)
2.将抛物线y=2
(x+1)2-3向右平移1个单位,再向上平移3个单位,则所得抛物线的表达式为____________________
3.足球守门员大脚开出去的球的高度随时间的变化而变化,这一过程可近似地用下列哪幅图表示(
)
A
B
C
D
5.一条抛物线的对称轴是x=1,且与x轴有唯一的公共点,并且开口方向向下,则这条抛物线的解析式为____________________________.(任写一个)
【学习目标】
1、掌握把抛物线平移至+k的规律并掌握二次函数的顶点式y=a
(x-h)2+k的图象的性质
2、通过独立思考、合作交流探索图象平移的规律和图象的性质,逐步培养学生分析问题、解决问题的能力。
3、渗透数形结合的数学思想,培养学生良好的学习习惯。
【重点】y=a(x-h)2+k的图象性质
【难点】a、h与k对二次函数图象的影响。
【预习】
一、学法指导:
1.认真阅读课本13——15页,15分钟时间自主探究课本的基础知识,在课本上做好勾画,完成课本上15页的练习题、习题。
2、完成教材助读设置的问题。
二、教材助读:
1、将抛物线如何平移可得到+1的图象?
2、二次函数的顶点式y=a
(x-h)2+k的图象的开口方向,对称轴,顶点坐标分别是什么?
三、预习自测(见课件)
1、将函数的图象向_____平移_____个单位可得函数的图象,再向_____平移____个单位可得函数+1的图象。
2.
y=-
(x+5)2-4函数图像的开口方向
,对称轴是
,顶点坐标是
。
【探究】
探究点一:图像的平移
在同一直角坐标系中,画出下列函数的图象,y=-x2,
y=-(x+1)2
,y=-(x+1)2-2.
x
…
-2
-1
0
1
2
…
y=-x2
…
…
y=-(x+1)2-2
由图象归纳:
1、它们的开口方向都向
,对称轴分别为
、
、
,
顶点坐标分别为
、
、
.
2、将函数的图象向_____平移_____个单位可得函数的图象,再向_____平移____个单位可得函数的图象。
3、把抛物线y=-x2向______平移______个单位,再向_______平移_______个单位,就得到抛物线y=-(x+1)2-2.(注意本题可有不同解答方式哟!)
学法指导:。
二次函数的图象的上下平移,只影响二次函数+k中k的值;左右平移,只影响h的值,抛物线的形状不变,所以平移时,可根据顶点坐标的改变,确定平移前、
后的函数关系式及平移的路径.此外,图象的平移与平移的顺序无关.
拓展:1、顶点坐标为(-2,3),开口方向和大小与抛物线y=x2相同的解析式为(
)
A.y=(x-2)2+3
B.y=(x+2)2-3
C.y=(x+2)2+3
D.y=-(x+2)2+3
探究点二:二次函数的顶点式y=a
(x-h)2+k的图象的性质
例2:函数y=2(x+3)2-5的a=
,h=
,
k=
.对称轴是
,顶点坐标是
,当X=___
__时函数值y有最
值是
.
当X__
___时,y随着X的增大而增大。
归纳:函数+k(a、h、k是常数,a≠0)的图象的开口方向、对称轴、顶点坐标与最值
+k
开口方向
对称轴
顶点坐标
最值
当x=____时y有最___值_____
当x=____时y有最___值_____
拓展训练:函数+k图象的顶点坐标为,并且经过点
(1)
求出a
,
h
,
k值,并写出函数的关系式
(2)函数的对称轴是______,当x______时,y随着x的增大而增大;当x=_____时y有最____值是______。
四、当堂检测
1、抛物线y=6x2+3与y=6
(x-1)2+10_____________相同,而____________不同.
2、抛物线y=-3
(x+4)2+1中,当x=_______时,y有最________值是________.
3、若抛物线y=a
(x-1)2+k上有一点A(3,5),则点A关于对称轴对称点A′的坐标为_____________.
五、训练
1、
y=3x2
y=-x2+1
y=(x+2)2
y=-4
(x-5)2-3
开口方向
顶点
对称轴
最值
增减性
(对称轴左侧)
2.将抛物线y=2
(x+1)2-3向右平移1个单位,再向上平移3个单位,则所得抛物线的表达式为____________________
3.足球守门员大脚开出去的球的高度随时间的变化而变化,这一过程可近似地用下列哪幅图表示(
)
A
B
C
D
5.一条抛物线的对称轴是x=1,且与x轴有唯一的公共点,并且开口方向向下,则这条抛物线的解析式为____________________________.(任写一个)
