4.1比例线段(1)

(共17张PPT)
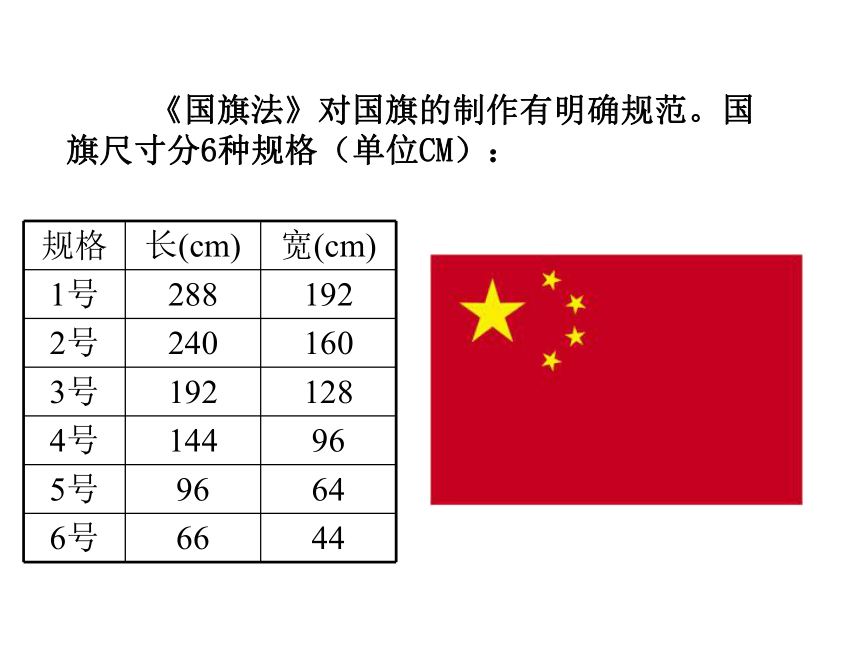
《国旗法》对国旗的制作有明确规范。国旗尺寸分6种规格（单位CM）：
规格 长(cm) 宽(cm)
1号 288 192
2号 240 160
3号 192 128
4号 144 96
5号 96 64
6号 66 44
组织引导者：
西郊中学 王晓辉
9︰12 =
6︰8 =
9︰12 = 6︰8
3︰4
3︰4
已知:a=-2,b=6,c=3,d=-9,
求a：b和c：d
结论：a：b=c：d或
a c
b d
=
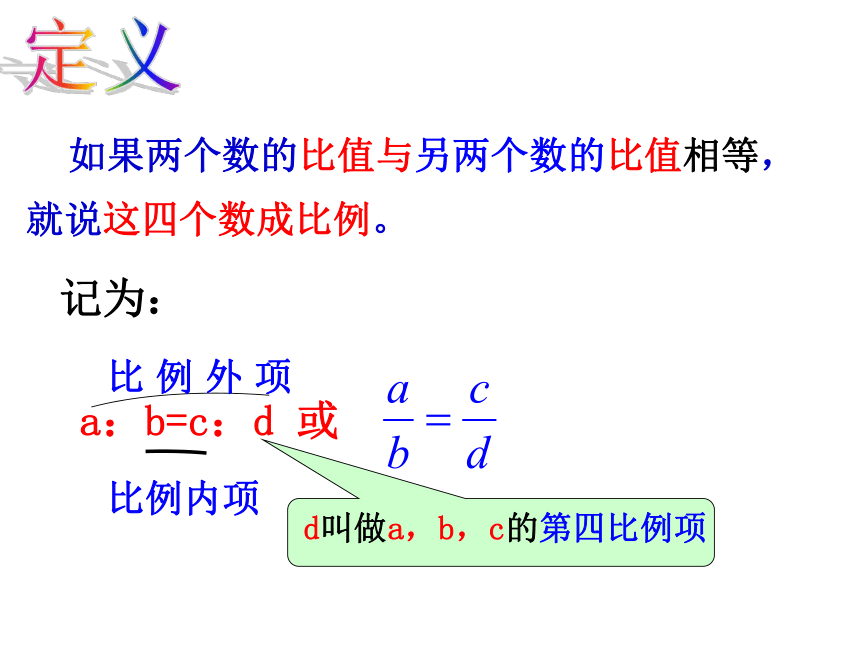
如果两个数的比值与另两个数的比值相等， 就说这四个数成比例。
a：b=c：d 或
比例内项
比 例 外 项
d叫做a，b，c的第四比例项
记为：
1、请指出下列比例式的比例内项和比例外项,并比较它们的积.
做一做
2、利用等式性质，能从 推导出ad=bc吗？反过来呢
比例的基本性质：
ad=bc
（a，b，c，d都不为零）
规定：本教科书中比例式的字母都约定取值不为零
上式从左到右是根据比例的两个外项之积等于两个内项之积或等式的性质得到，那么从右到左的推理是唯一的形式吗？
看谁想的多：
已知 a·d=b·c，你能得到哪些比例式
对调内项，
比例仍成立！
对调外项，
比例还成立吗？
a
b
c
d
=
b
a
d
c
=
b
d
a
c
=
c
d
a
b
=
d
b
c
a
=
a
c
b
d
=
c
a
d
b
=
d
c
b
a
=
例1（1）根据下列条件,求a:b的值.
（2）求下列比例式中的 x.
例2、已知 判断下列比例式是否
成立,并说明理由
解（1）比例式成立，理由如下
两边同加1，得：
即：
（2）设 =k，则a=bk，c=dk
比例式变形的常用方法:
利用等式性质
设比值
k
练一练
1、已知 ，求 的值。
2、若比例式 0，求 的值。
课堂小结:
(a,b,c,d均不为零)
比例有如下性质:
比例式变形的常用方法:
利用等式性质
设比值
k
作业
1，课本中作业题
2，作业本
探究活动
在平面直角坐标系中,过点(a,b)和原点的直线是一个怎样的正比例函数的图象 如果a,b,c,d四个数成比例,你认为点(a,b),点(c,d)和原点在同一条直线上吗
解：点（a，b），点（c，d）和坐标原点在同一条直线y＝ x上。理由：
∴原点，（a，b），（c，d）在同一直线上
显然(c,d)在直线y＝ x上
∴直线y＝ x也可以表示为y＝ x
∵a，b，c，d成比例 ∴ k＝ =
则k＝
∴y＝ x
设经过点（a，b）和原点的直线为y＝kx
2.已知x:y:z=4:5:7,求 ，
3.已知x：y=3：4，x：z=2：3，
求x：y：Z的值。
1.已知
,求
拓展练习