1.2有关三角函数的计算(2)
图片预览





文档简介
(共15张PPT)
如图,将一个Rt△ABC形状的楔子从木桩的底端点
P沿着水平方向打入木桩底下,可以使木桩向上运
动,如果木桩向上运动了1cm,楔子沿水平方向前进
5cm(如箭头所示),那么楔子的倾斜角为多少度
解 由题意得,当楔子沿水平方向前进5cm,即BN=5cm时,
木桩上升的距离为PN,即PN=1cm.
C
A
F
P
B
N
∠B=
F
P
B
C
A
在Rt△PBN中,
∵tanB= =
新课引入
已知锐角三角函数值求角的度数
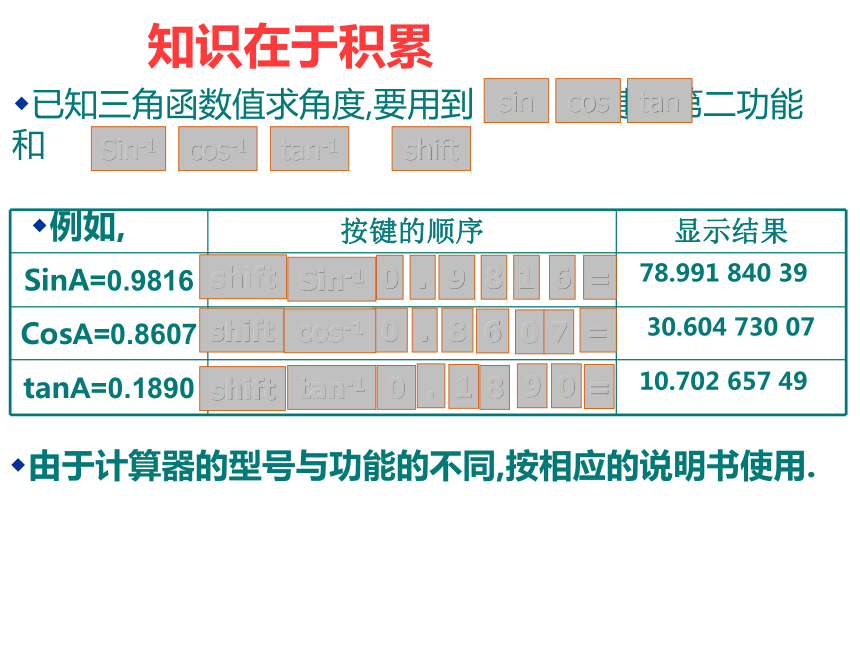
知识在于积累
已知三角函数值求角度,要用到 键的第二功能 和 键 .
例如,
由于计算器的型号与功能的不同,按相应的说明书使用.
sin
cos
tan
按键的顺序 显示结果
SinA=0.9816
CosA=0.8607
tanA=0.1890
shift
0
.
78.991 840 39
shift
0
.
30.604 730 07
shift
0
.
10.702 657 49
9
8
1
Sin-1
cos-1
tan-1
shift
8
1
6
=
6
0
7
=
8
9
0
=
Sin-1
cos-1
tan-1
那么上题中的∠B是多少度呢
∠B≈11.310
由锐角三角函数值求锐角:
1、已知tan x=0.7410,求锐角x.(精确到1′)
解:
按下列顺序
依次按键:
显示结果为36.538 445 77.
再按键:
显示结果为36゜32′18.4.
所以,x≈36゜32′.
根据下面的条件,求锐角α的大小(精确到1")
(1)sin α=0.4511
(2)cos α=0.7857
(3)tan α=1.4036
shift
sin
0
.
4
5
1
1
=
0'''
shift
cos
0
.
7
8
5
7
=
0'''
shift
tan
1
.
4
0
3
6
=
0'''
老师提示:上表的显示结果是以度为单位的,再按 键即可显示以“度,分,秒”为单位的结果.
0'''
例2
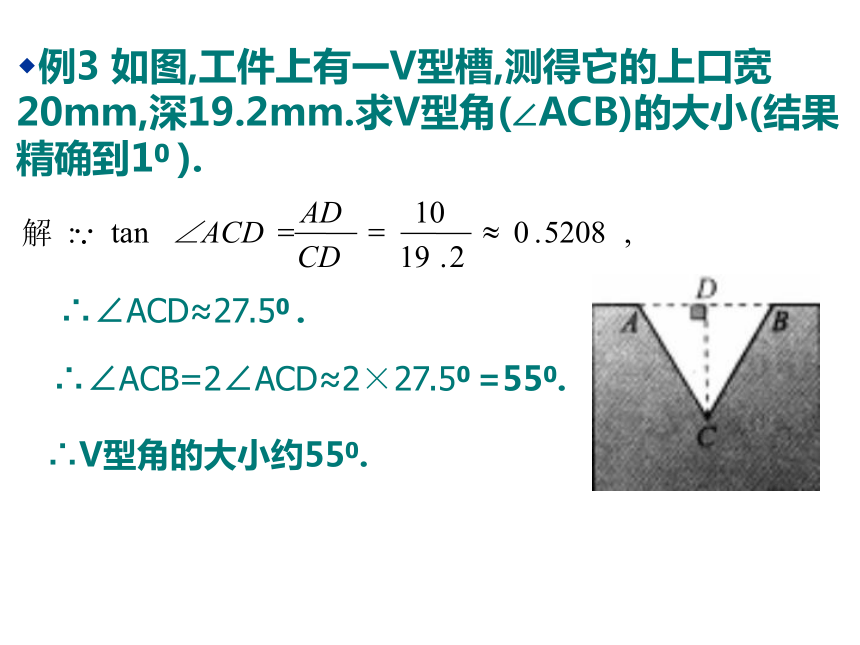
例3 如图,工件上有一V型槽,测得它的上口宽20mm,深19.2mm.求V型角(∠ACB)的大小(结果精确到10 ).
∴∠ACD≈27.50 .
∴∠ACB=2∠ACD≈2×27.50 =550.
∴V型角的大小约550.
,
5208
.
0
2
.
19
10
tan
:
=
=
CD
AD
∠ACD
Q
解
例4.如图,一段公路弯道呈圆弧形,测得弯道
AB两端的距离为200m,AB的半径为1000m,求弯道的长(精确到0.1m)
A
B
O
R
C
加强巩固
由锐角的三角函数值反求锐角
填表:已知一个角的三角函数值,求这个角的度数(逆向思维)
∠A= ∠A= ∠A=
∠A= ∠A= ∠A=
∠A= ∠A= ∠A=
练一练
1.sin700=
cos500=
(3)tanA= ,则A=
(4)2sinA- =0,则A=
2.(1)sinA=0.3475 ,则A= (精确到1")
(2)cosA=0.4273,则A= (精确到1")
0.9397
0.6428
20020'4"
64042'13"
300
600
练一练
3.已知sinα.cos300= ,求锐角α
4. 一梯子斜靠在一面墙上,已知梯子长4m,梯子位于地面上的一端离墙壁2.5m,求梯子与地面所成的锐角.
5. 如图,根据图中已知数据,求AD.
A
B
C
550
250
20
D
┌
6.如图,物华大厦离小伟家60m,小伟从自家的窗中眺望大厦,并测得大厦顶部仰角是450,而大厦底部的俯角是370,求该大厦的的高度 (结果精确到0.1m).
老师提示:当从低处观察高处的目标时.视线与水平线所成的锐角称为仰角.当从高处观察低处的目标时.视线与水平线所成的锐角称为俯角.
真知在实践中诞生
3. 图中的螺旋形由一系列直角三角形组成.每个三角形都以点O为一顶点.
(1)求∠A0OA1,∠A1OA2,∠A2OA3,的大小.
(2)已知∠An-1OAn,是一个小于200的角,求n的值.
如图,将一个Rt△ABC形状的楔子从木桩的底端点
P沿着水平方向打入木桩底下,可以使木桩向上运
动,如果木桩向上运动了1cm,楔子沿水平方向前进
5cm(如箭头所示),那么楔子的倾斜角为多少度
解 由题意得,当楔子沿水平方向前进5cm,即BN=5cm时,
木桩上升的距离为PN,即PN=1cm.
C
A
F
P
B
N
∠B=
F
P
B
C
A
在Rt△PBN中,
∵tanB= =
新课引入
已知锐角三角函数值求角的度数
知识在于积累
已知三角函数值求角度,要用到 键的第二功能 和 键 .
例如,
由于计算器的型号与功能的不同,按相应的说明书使用.
sin
cos
tan
按键的顺序 显示结果
SinA=0.9816
CosA=0.8607
tanA=0.1890
shift
0
.
78.991 840 39
shift
0
.
30.604 730 07
shift
0
.
10.702 657 49
9
8
1
Sin-1
cos-1
tan-1
shift
8
1
6
=
6
0
7
=
8
9
0
=
Sin-1
cos-1
tan-1
那么上题中的∠B是多少度呢
∠B≈11.310
由锐角三角函数值求锐角:
1、已知tan x=0.7410,求锐角x.(精确到1′)
解:
按下列顺序
依次按键:
显示结果为36.538 445 77.
再按键:
显示结果为36゜32′18.4.
所以,x≈36゜32′.
根据下面的条件,求锐角α的大小(精确到1")
(1)sin α=0.4511
(2)cos α=0.7857
(3)tan α=1.4036
shift
sin
0
.
4
5
1
1
=
0'''
shift
cos
0
.
7
8
5
7
=
0'''
shift
tan
1
.
4
0
3
6
=
0'''
老师提示:上表的显示结果是以度为单位的,再按 键即可显示以“度,分,秒”为单位的结果.
0'''
例2
例3 如图,工件上有一V型槽,测得它的上口宽20mm,深19.2mm.求V型角(∠ACB)的大小(结果精确到10 ).
∴∠ACD≈27.50 .
∴∠ACB=2∠ACD≈2×27.50 =550.
∴V型角的大小约550.
,
5208
.
0
2
.
19
10
tan
:
=
=
CD
AD
∠ACD
Q
解
例4.如图,一段公路弯道呈圆弧形,测得弯道
AB两端的距离为200m,AB的半径为1000m,求弯道的长(精确到0.1m)
A
B
O
R
C
加强巩固
由锐角的三角函数值反求锐角
填表:已知一个角的三角函数值,求这个角的度数(逆向思维)
∠A= ∠A= ∠A=
∠A= ∠A= ∠A=
∠A= ∠A= ∠A=
练一练
1.sin700=
cos500=
(3)tanA= ,则A=
(4)2sinA- =0,则A=
2.(1)sinA=0.3475 ,则A= (精确到1")
(2)cosA=0.4273,则A= (精确到1")
0.9397
0.6428
20020'4"
64042'13"
300
600
练一练
3.已知sinα.cos300= ,求锐角α
4. 一梯子斜靠在一面墙上,已知梯子长4m,梯子位于地面上的一端离墙壁2.5m,求梯子与地面所成的锐角.
5. 如图,根据图中已知数据,求AD.
A
B
C
550
250
20
D
┌
6.如图,物华大厦离小伟家60m,小伟从自家的窗中眺望大厦,并测得大厦顶部仰角是450,而大厦底部的俯角是370,求该大厦的的高度 (结果精确到0.1m).
老师提示:当从低处观察高处的目标时.视线与水平线所成的锐角称为仰角.当从高处观察低处的目标时.视线与水平线所成的锐角称为俯角.
真知在实践中诞生
3. 图中的螺旋形由一系列直角三角形组成.每个三角形都以点O为一顶点.
(1)求∠A0OA1,∠A1OA2,∠A2OA3,的大小.
(2)已知∠An-1OAn,是一个小于200的角,求n的值.
