1.1锐角三角函数
图片预览

文档简介
(共18张PPT)
*
第一章 解直角三角形
1.1 锐角三角函数
A
B1
C1
C
B
想一想
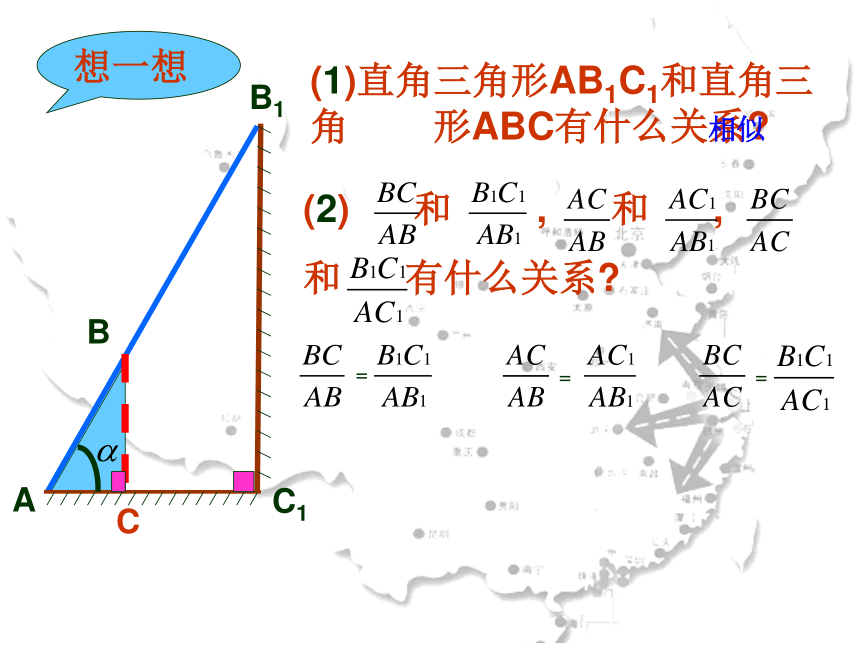
(1)直角三角形AB1C1和直角三角 形ABC有什么关系
(2) 和 , 和 ,
和 有什么关系
相似
=
=
=
A
B1
C1
想一想
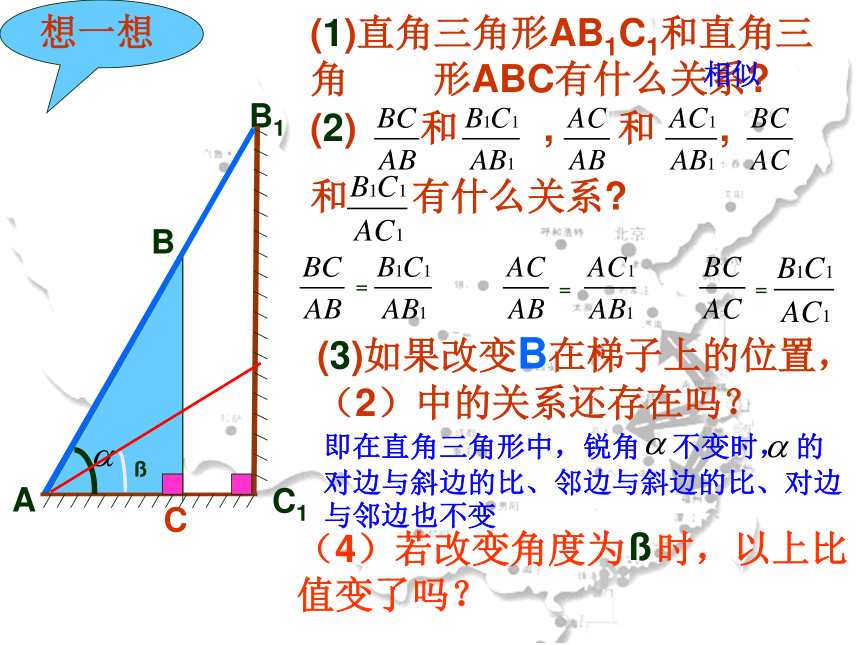
(1)直角三角形AB1C1和直角三角 形ABC有什么关系
(2) 和 , 和 ,
和 有什么关系
(3)如果改变B在梯子上的位置,(2)中的关系还存在吗?
C
B
=
=
=
相似
即在直角三角形中,锐角 不变时, 的对边与斜边的比、邻边与斜边的比、对边与邻边也不变
(4)若改变角度为 时,以上比值变了吗?
A
α
B
C
α
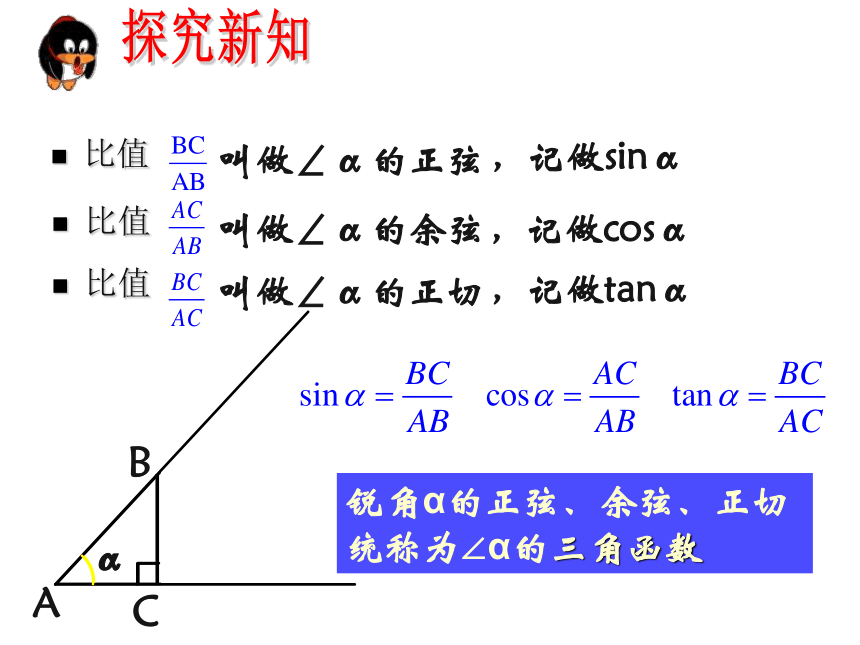
比值
比值
比值
A
叫做∠α的正弦
,记做sinα
B
C
叫做∠α的余弦
,记做cosα
叫做∠α的正切
,记做tanα
锐角α的正弦、余弦、正切
统称为∠α的三角函数
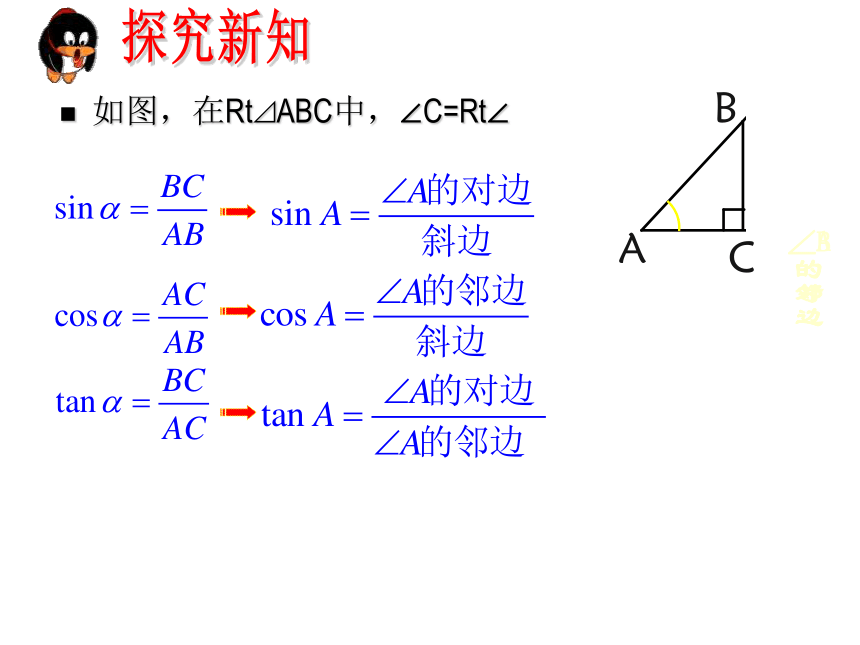
如图,在Rt⊿ABC中,∠C=Rt∠
A
B
C
∠A
的
对
边
∠B
的
邻
边
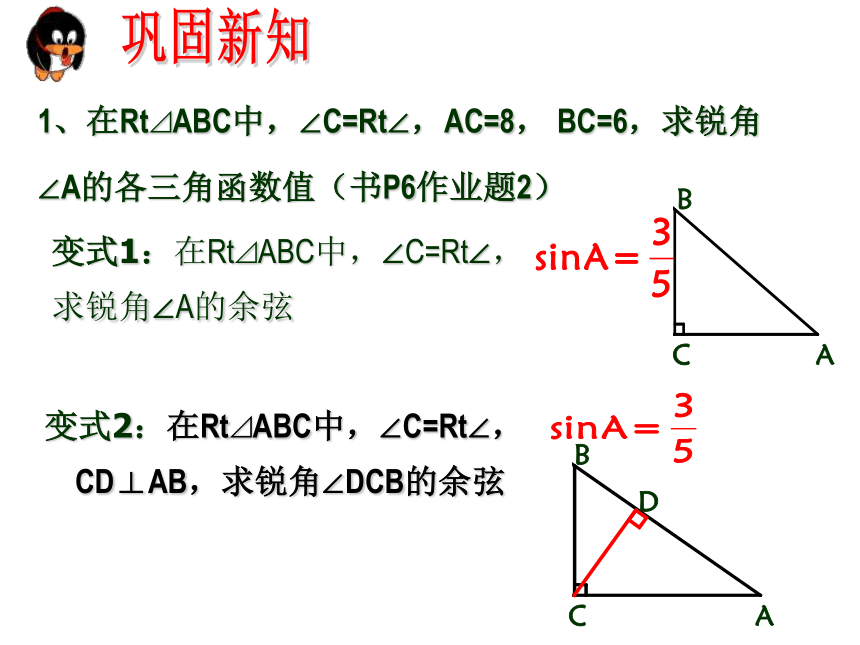
1、在Rt⊿ABC中,∠C=Rt∠,AC=8, BC=6,求锐角
∠A的各三角函数值(书P6作业题2)
变式1:在Rt⊿ABC中,∠C=Rt∠,
求锐角∠A的余弦
B
C
A
变式2:在Rt⊿ABC中,∠C=Rt∠, CD⊥AB,求锐角∠DCB的余弦
B
C
A
D
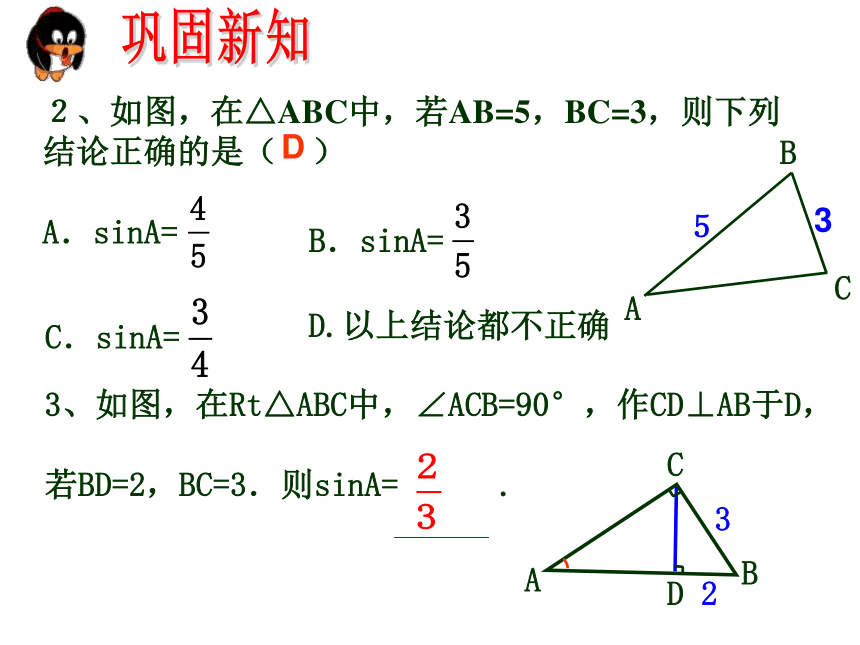
2、如图,在△ABC中,若AB=5,BC=3,则下列
结论正确的是( )
A.sinA=
B.sinA=
C.sinA=
D.以上结论都不正确
C
A
B
3
5
D
3、如图,在Rt△ABC中,∠ACB=90°,作CD⊥AB于D,
若BD=2,BC=3.则sinA= .
3
D
B
C
A
2
4.如图,在△ABC中,AB=15,AC=13, S△ABC=84,
求sinA的值。
A
B
C
sinα= ,
cosα= ,
tanα=
5.已知锐角α的始边在x轴的正半轴上,(顶点在原点)终边上一点P的坐标为(2, 3),求角α的三个三角函数值。
x
y
P
O
α
(2,3)
M
解:过P作OM⊥x轴于M,则OM=2,PM=
3 ,∴OP=√22+32=√13
1.如图,在Rt△ABC中,锐角A的对边和邻边同时扩大100倍,tanA的值( )
A.扩大100倍 B.缩小100倍
C.不变 D.不能确定
2.已知∠A,∠B为锐角
(1)若∠A=∠B,则tanA tanB;
(2)若tanA=tanB,则∠A ∠B.
A
B
C
┌
3.在Rt△ABC中,∠C=90°,AB=15,tanA= ,
求AC和BC.
4.在等腰△ABC,AB=AC=13,BC=10,
求tanB. sinB
A
C
B
┌
D
5. 在Rt△ABC中,∠C=90°.
(1)AC=25.AB=27.求tanA和tanB. sinA
(2)BC=3, sinA =0.6,求AC 和AB.
(3)AC=4,tanA=0.8,求BC.
6.在梯形ABCD中,AD//BC,AB=DC=13,
AD=8,BC=18.求:tanB. sinB
A
D
B
C
F
┌
E
┌
我
来
说
经历了一个探究过程:特殊到一般
学习了一个重要概念:锐角三角函数
∠α的正弦
∠α的余弦
∠α的正切
在本节课中,我们……
体现了一种数学思想:数形结合
体验到一种学习方法:猜想 证明 归纳 应用
书面作业:
教科书P6中的作业题。(必做题)
探究作业:
1.对锐角α,请思考tanα的取值范围是多少?
2.在Rt△ABC中,∠C=Rt∠,当∠A=α时,
比值 也是锐角α的函数吗?(选做题)
*
谢 谢
2008.12.11
甲、乙两队分别在倾斜角为30°和50°的斜坡上都步行了150米,那么乙队比甲队高多少米?
30°
150米
甲队
50°
乙队
150米
50°
150米
A
C
B
75米
30°
50°
甲队
600米
A
乙队
拓展问题1:如图,已知甲队步行了600米到达山顶C处请问乙队要步行多少米才能到达山顶?
?
B
拓展问题2:利用图中的数据,若测得∠PAD的度数,就能求出塔高PC,你能说出其中的道理吗?
C
D
P
*
第一章 解直角三角形
1.1 锐角三角函数
A
B1
C1
C
B
想一想
(1)直角三角形AB1C1和直角三角 形ABC有什么关系
(2) 和 , 和 ,
和 有什么关系
相似
=
=
=
A
B1
C1
想一想
(1)直角三角形AB1C1和直角三角 形ABC有什么关系
(2) 和 , 和 ,
和 有什么关系
(3)如果改变B在梯子上的位置,(2)中的关系还存在吗?
C
B
=
=
=
相似
即在直角三角形中,锐角 不变时, 的对边与斜边的比、邻边与斜边的比、对边与邻边也不变
(4)若改变角度为 时,以上比值变了吗?
A
α
B
C
α
比值
比值
比值
A
叫做∠α的正弦
,记做sinα
B
C
叫做∠α的余弦
,记做cosα
叫做∠α的正切
,记做tanα
锐角α的正弦、余弦、正切
统称为∠α的三角函数
如图,在Rt⊿ABC中,∠C=Rt∠
A
B
C
∠A
的
对
边
∠B
的
邻
边
1、在Rt⊿ABC中,∠C=Rt∠,AC=8, BC=6,求锐角
∠A的各三角函数值(书P6作业题2)
变式1:在Rt⊿ABC中,∠C=Rt∠,
求锐角∠A的余弦
B
C
A
变式2:在Rt⊿ABC中,∠C=Rt∠, CD⊥AB,求锐角∠DCB的余弦
B
C
A
D
2、如图,在△ABC中,若AB=5,BC=3,则下列
结论正确的是( )
A.sinA=
B.sinA=
C.sinA=
D.以上结论都不正确
C
A
B
3
5
D
3、如图,在Rt△ABC中,∠ACB=90°,作CD⊥AB于D,
若BD=2,BC=3.则sinA= .
3
D
B
C
A
2
4.如图,在△ABC中,AB=15,AC=13, S△ABC=84,
求sinA的值。
A
B
C
sinα= ,
cosα= ,
tanα=
5.已知锐角α的始边在x轴的正半轴上,(顶点在原点)终边上一点P的坐标为(2, 3),求角α的三个三角函数值。
x
y
P
O
α
(2,3)
M
解:过P作OM⊥x轴于M,则OM=2,PM=
3 ,∴OP=√22+32=√13
1.如图,在Rt△ABC中,锐角A的对边和邻边同时扩大100倍,tanA的值( )
A.扩大100倍 B.缩小100倍
C.不变 D.不能确定
2.已知∠A,∠B为锐角
(1)若∠A=∠B,则tanA tanB;
(2)若tanA=tanB,则∠A ∠B.
A
B
C
┌
3.在Rt△ABC中,∠C=90°,AB=15,tanA= ,
求AC和BC.
4.在等腰△ABC,AB=AC=13,BC=10,
求tanB. sinB
A
C
B
┌
D
5. 在Rt△ABC中,∠C=90°.
(1)AC=25.AB=27.求tanA和tanB. sinA
(2)BC=3, sinA =0.6,求AC 和AB.
(3)AC=4,tanA=0.8,求BC.
6.在梯形ABCD中,AD//BC,AB=DC=13,
AD=8,BC=18.求:tanB. sinB
A
D
B
C
F
┌
E
┌
我
来
说
经历了一个探究过程:特殊到一般
学习了一个重要概念:锐角三角函数
∠α的正弦
∠α的余弦
∠α的正切
在本节课中,我们……
体现了一种数学思想:数形结合
体验到一种学习方法:猜想 证明 归纳 应用
书面作业:
教科书P6中的作业题。(必做题)
探究作业:
1.对锐角α,请思考tanα的取值范围是多少?
2.在Rt△ABC中,∠C=Rt∠,当∠A=α时,
比值 也是锐角α的函数吗?(选做题)
*
谢 谢
2008.12.11
甲、乙两队分别在倾斜角为30°和50°的斜坡上都步行了150米,那么乙队比甲队高多少米?
30°
150米
甲队
50°
乙队
150米
50°
150米
A
C
B
75米
30°
50°
甲队
600米
A
乙队
拓展问题1:如图,已知甲队步行了600米到达山顶C处请问乙队要步行多少米才能到达山顶?
?
B
拓展问题2:利用图中的数据,若测得∠PAD的度数,就能求出塔高PC,你能说出其中的道理吗?
C
D
P
