二次函数的应用复习

(共19张PPT)
二次函数的应用
组织引导者：
新昌县西郊中学 王晓辉
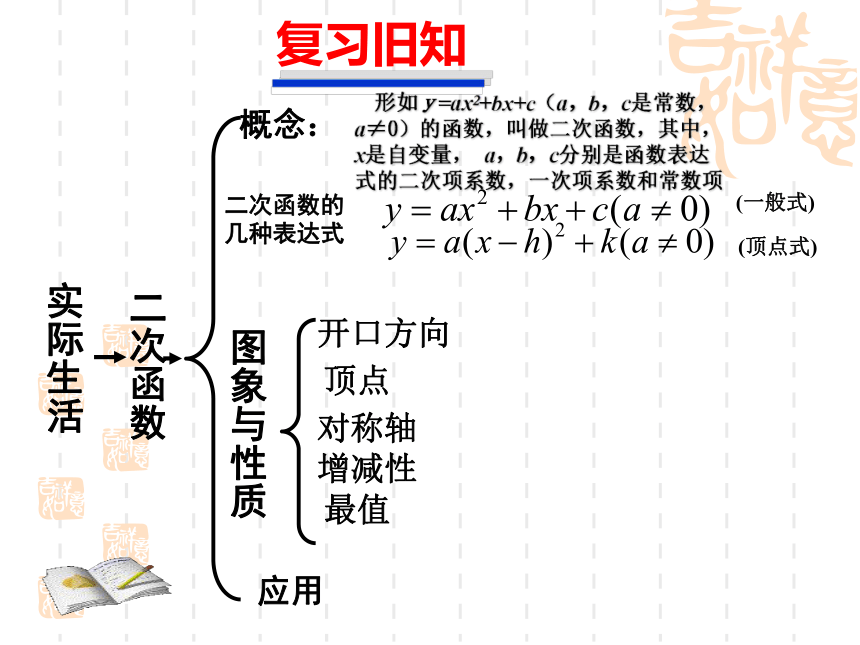
实际生活
二次函数
图象与性质
概念：
开口方向
顶点
对称轴
增减性
最值
应用
复习旧知
形如ｙ=ax2+bx+c（a，b，c是常数，a≠0）的函数，叫做二次函数，其中，x是自变量， a，b，c分别是函数表达式的二次项系数，一次项系数和常数项
二次函数的
几种表达式
(一般式)
(顶点式)
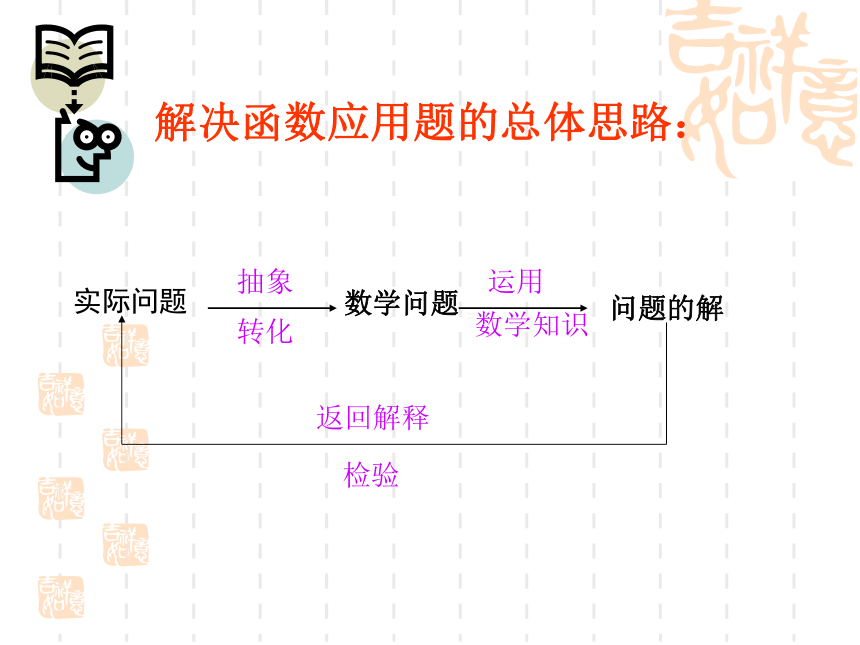
实际问题
抽象
转化
数学问题
运用
数学知识
问题的解
返回解释
检验
解决函数应用题的总体思路：
解决函数应用题的具体步骤：
第二步建立函数的解析式；
第三步确定自变量的取值范围；
第四步根据顶点坐标公式或配方法
求出最大值或最小值（在自变量的
取值范围内）或者利用函数的其他知识求解。
第五步验证、答题
第一步设自变量；
二次函数的应用非常广泛
典型的题型有以下几种：
1.最优化问题
2、利用二次函数与一元二次方程两种数学模式的转换来解决实际问题。
3在距离、利润等问题中的函数最值问题
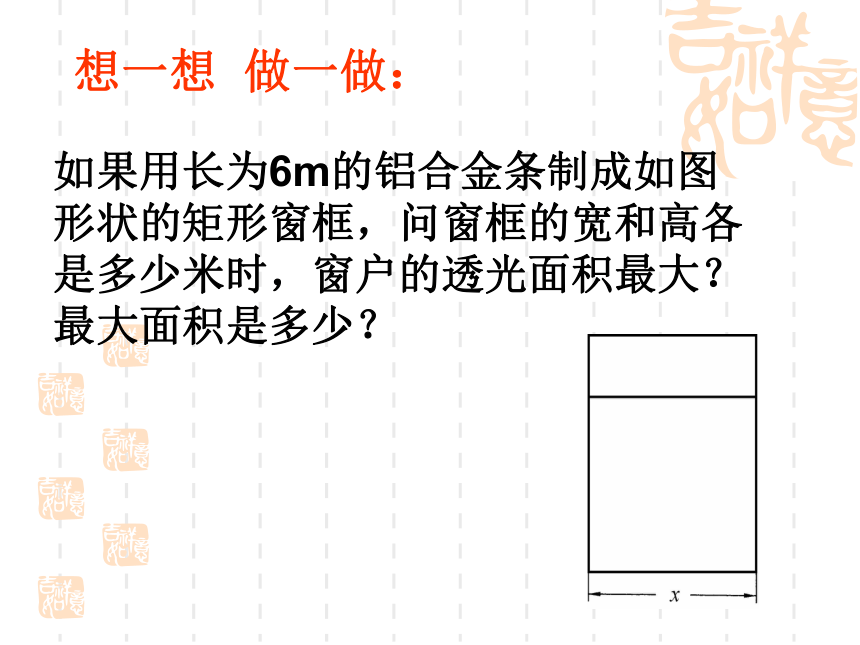
现有长6米的铝合金条，设问：
请你用它制成一矩形窗框，
怎样设计，窗框的透光面积最大？
x
3-x
y=x(3-x)
=-x2 +3x
(0＜x＜3)
解:设宽为x米,则长为(x-3)米根据题意得,
当x = 时,y有最大值是
最优化问题
如果用长为6m的铝合金条制成如图形状的矩形窗框，问窗框的宽和高各是多少米时，窗户的透光面积最大？最大面积是多少？
想一想 做一做：
二次函数y=ax +bx+c
问题2： 二次函数与一元二次方程的关系问题解决实际问题
y=0
一元二次方程ax +bx+c=0
两根为x1=m；x2=n
函数与x轴交点坐标为：
（m，0）；（n，0）
例2.(连云港) 丁丁推铅球的出手高度为
,在如图
①求k的值
所示的直角坐标系中，铅球的运行路线近似为抛物线
x
y
O
②求铅球的落地点Ａ与丁 丁的水平距离
③ 当铅球高度为1.6米时，铅球与
丁丁的水平距离是多少？(如图)，
(0，1.6)
A
①求k的值
x
y
O
解：由图像可知，抛物线过点(0,1.6)
即当x=0时，y=1.6,
1.6=-0.1k+2.5,
k=±3.
又因为对称轴是在y轴的右侧，
即x=k>0,
所以，k=3.
2
②-0.1(x-3)+2.5=0，
解之得，x =8,x =-2，
所以，OA=8，
故铅球的落地点与丁丁的距离是8米.
2
2
1
③当y=1.6时，
1.6=-0.1(x-3)+2.5
x=0, 6
2
答，当铅球高度是1.6米事，距离出手点的水平距离为0米或6米。
A
例3 某饮料经营部每天的固定费用为200元,其销售的饮料
每瓶进价为5元。销售单价与日均销售量的关系如下
销售单价(元) 6 7 8 9 10 11 12
日均销售量(瓶) 480 440 400 360 320 280 240
(1)若记销售单价比每瓶进价多x元时，日均毛利润
(毛利润＝单个利润X销售量－固定费用)为y元，求y关于x的函数解析式和自变量的取值范围；
(2)若要使日均毛利润达到最大，销售单价应定为多
少元(精确到0.1元)？最大日均毛利润为多少？
问题3：距离、利润等问题中的函数最值问题
销售单价(元) 6 7 8 9 10 11 12
日均销售量(瓶) 480 440 400 360 320 280 240
例3某饮料经营部每天的固定成本为200元,其销售的饮料每瓶进价为5元。销售
单价与日均销售量的关系如下
(1)若记销售单价比每瓶进价多x元时，日均毛利润(毛利润＝售价－进价－固定
成本)为y元，求y关于x的函数解析式和自变量的取值范围
解:
(1)由题意,销售单价每增加1元,日均销售量就减少40瓶.当销售
单价比进价多X元时,与销售单价6元时相比,日均销售量为
（瓶）.
销售单价(元) 6 7 8 9 10 11 12
日均销售量(瓶) 480 440 400 360 320 280 240
例3某饮料经营部每天的固定费用为200元,其销售的饮料每瓶进价为5元。销售
单价与日均销售量的关系如下
(2)若要使日均毛利润达到最大，销售单价应定为多少元(精确到0.1元)？
最大日均毛利润为多少？
解:(2)
由第(1)题,得
答:若要使日均毛利润达到最大,销售单价应定为11.5元,
最大日均毛利润为1490元.
1.数形结合是本章主要的数学思想，通过画图将二次函数直观表
示出来，根据函数图象，就能知道函数的开口方向、顶点坐标、
对称轴、变化趋势、与坐标轴的交点、函数的最值等问题.
2.待定系数法是本章重要的解题方法，要能通过三个条件确定二
次函数的关系式；灵活根据题中的条件，设出适合的关系式.
3.建模思想在本章有重要的应用，将实际问题通过设自变量，建立函数关系，转化为二次函数问题，再利用二次函数的性质解决问题.
回顾反思：
1、.解答函数应用题时，要充分地对题目所提供的信息进行梳理，提取有效信息加以分析，对问题的原始形状进行抽象、联想和概括，构建相应的数学模型即函数关系，并利用已学过的数学知识加以解决。
2、对一些函数应用题常常要结合已知条件写出自变量的取值范围，以此确定这些函数区间的最值情况，利用函数知识解决实际问题时，答案要结合实际问题的意义进行检验。
归纳总结：
1、 已知有一张边长为10cm的正三角形纸板，若要从中剪一个面积最大的矩形纸板，应怎样剪？最大面积为多少？
A
B
C
D
E
F
K
2、利用函数图象判断下列方程有没有解，有几个解。若有解，求出它们的解（精确到0.1）。
①X =2x-1
②2x -x+1=0
③2x -4x-1=0
课后思考
3、在矩形荒地ABCD中，AB=10，BC=6,今在四边上分别选取E、F、G、H四点，且AE=AH=CF=CG=x，建一个花园，如何设计，可使花园面积最大？
D
C
A
B
G
H
F
E
10
6
解：设花园的面积为y
则 y=60-x2 -（10-x）（6-x）
=-2x2 + 16x
（0=-2(x-4)2 + 32
所以当x=4时 花园的最大面积为32
同学们：作业布置，课后另行安排