一次函数的复习

(共11张PPT)
课题: 一次函数复习课(一)
1、已知函数y=(a-1)x+a+1,
当a满足 时，它为一次函数；
当a满足 时，它为正比例函数。
在解答下列各小题过程中，回顾用到了哪些知识点？
a≠1
a=-1
定义:函数y=kx ＋b (k、b为常数，k ≠０)叫做一次函数。
当b =０ 时，函数y=kx(k ≠０)叫做正比例函数。
2、已知正比例函数y=kx，当x=-2时，y=6，则比例系数k=___
-3
3、点P（2，-3）在函数y=kx+1的图象上，则k= 。
-2
小结:已知一次函数的自变量和函数的一对对应值,可以求得一个字母系数的值.
点在函数图象上，则点的坐标一定满足函数解析式。
4、在如图所示平面直角坐标系中,
点A的坐标为 ,点B的坐标为 ;
直线AB的解析式是 .
y
x
o
1
2
1
A
B
一:回顾与总结
(0,1)
(2,0)
y=-0.5x+1
求解函数解析式的重要方法:_____________
待定系数法
待定系数法
解：
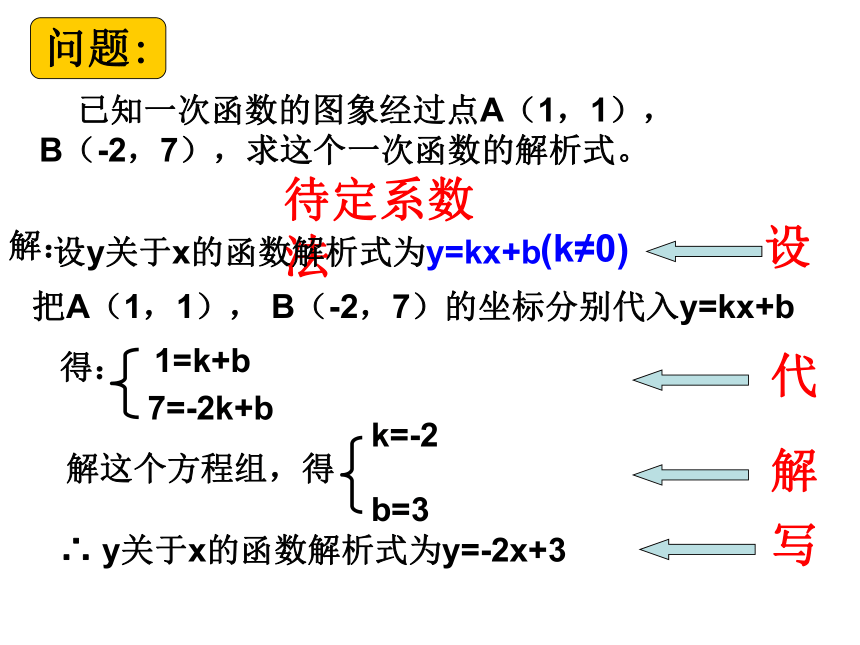
设y关于x的函数解析式为y=kx+b
把A（1，1）， B（-2，7）的坐标分别代入y=kx+b
得：
1=k+b
7=-2k+b
解这个方程组，得
k=-2
b=3
∴ y关于x的函数解析式为y=-2x+3
设
代
解
写
已知一次函数的图象经过点A（1，1），B（-2，7），求这个一次函数的解析式。
问题:
(k≠0)
同类变式一
1、已知y-6与x+2成正比例，且当x＝3时，y＝－4；求y关于x的函数解析式。
整体思想的运用
2、某产品每件成本10元，试销阶段每件产品的销售价x（元）与产品的日销售量y（件）之间的关系如下表：
若日销售量y是销售价x的一次函数．
①求出日销售量y(件)与销售价x(元)的函数关系式
②当销售价定为30元时，每日的销售量是多少
同类变式二
x （元） 15 20 25 …
y （件） 25 20 15 …
m
s
O
2
4
6
2
8
4
6
A
B
L
如图,线段AL表示弹簧的长度s(cm)与所挂物体的质量m(kg)之间的关系的图象,请结合图象回答下列问题:
(1):问题中的两个变量s与m之间是不是一次函数关系
(2):s与m之间的函数关系是_______________ _ ;
(3):由图知弹簧的原长是____cm.
(4):当所挂物体的质量为3kg时,弹簧的长度 s=___cm;
(kg)
(cm)
是
s=0.5m+6
7.5
归纳:
运用一次函数模型解决实际问题的基本步骤是：
6
根据图象判断函数的类型
用待定系数法求出函数解析式
解决有关函数的实际问题
同类变式三
(0≤m≤6)
富阳市自来水公司为鼓励居民节约用水,采取按月用水量分段收费办法,若居民应交水费y(元)与用水量x(吨)的函数关系如图所示.
(1):分别写出0≤x≤15和x≥15时,y与x的函数关系式;
(2):若某用户该月用水21吨,则应交水费多少元
O
15
20
39.5
27
x
吨
元
y
A
B
解题思路：
关键是识别自变量在不同的取值范围内所对应函数的类型
用待定系数法分别求出不同范围内的函数解析式
分段函数
尝试园地1:
本节课我们复习了哪些数学知识和数学思想方法
一、用待定系数法求函数解析式
设
代
解
写
步骤：
设y关于x的函数解析式为y=kx+b(k≠0)
把关于x，y的数对代入解析式，得到k，b的方程组
解关于k，b的方程组
把k，b的值代入y=kx+b(k≠0)，写出函数解析式
二、在具体的实际情景中,用一次函数解决问题
四、用整体思想解决 数学问题
课堂小结:
三、分段函数的解法
实际问题
求函数解析式
计算问题
如图反映的过程是：早上8：00小明从家跑步到体育馆，锻炼一阵后，散步走回家，其中t表示时间，S表示小明离家的距离。
（1）求出小明从家跑步到体育馆这段函数图象的解析式；
（2）求出小明散步回家这段函数图象的解析式；
（3）回答小明在体育馆用去的时间是多少分钟？
S（m）
0
2250
15
30
80
t（min）
A
B
C
O
（4）求小明离家1800m时的时间是几时几分
分类讨论的思想
1800
挑战题:
(勇敢的同学,发挥你的聪明智慧来挑战吧！)
某校八年级学生小丽、小强和小红到某超市参加了社会实践活动，在活动中他们参与了某种水果的销售工作，已知该水果的进价为8元/千克，下面是他们在活动结束后的对话。小丽：如果以10元/千克的价格销售，那么每天可售出300千克。小强：如果以13元/千克的价格销售，那么每天可获取利润750元。小红：通过调查验证，我发现每天的销售量y（千克）与销售单价x（元）之间存在一次函数关系。
（1）求y（千克）与x（元）（x＞0）的函数关系式；
（2）设该超市销售这种水果每天获取的利润为W元，那么当销售单价为何值时，每天可获得的利润最大？最大利润是多少元？【利润＝销售量×（销售单价－进价）】
思考题