1.3解直角三角形(1)
图片预览




文档简介
(共18张PPT)
三角函数定义
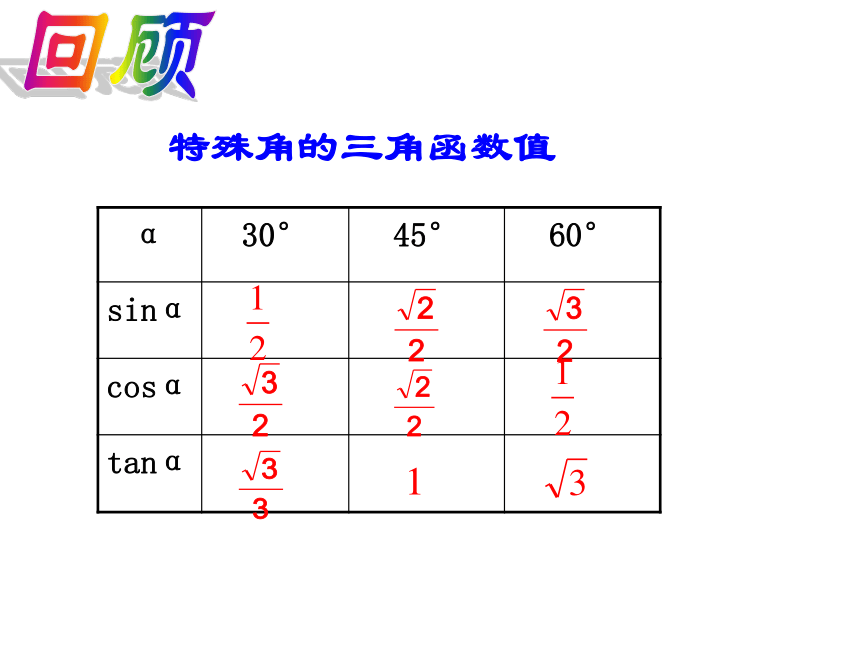
α 30° 45° 60°
sinα
cosα
tanα
特殊角的三角函数值
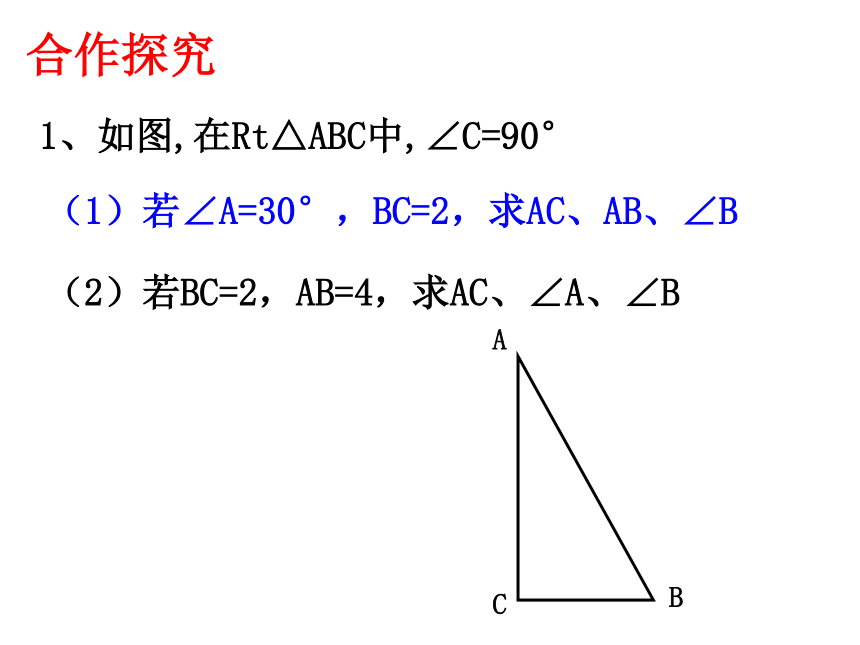
1、如图,在Rt△ABC中,∠C=90°
(1)若∠A=30°,BC=2,求AC、AB、∠B
A
C
B
(2)若BC=2,AB=4,求AC、∠A、∠B
合作探究
合作探究
2、已知在Rt△ABC中,∠C= Rt∠,AB=5,AC=3,求边BC的长。你能求出∠A的度数么?
3、已知在Rt△ABC中, ∠C= Rt∠ ,∠A=560,AB=8,求AC的长。
sin37°≈0.6,cos53 ° ≈ 0.6,tan30 °≈0.6
sin56°≈0.8290,cos56°≈ 0.5592,tan56°≈1.483
在上述例题中,我们都是利用直角三角形中的已知边、角来求出另外一些的边角.像这样,
********************************
在直角三角形中,由已知的一些边、角,求出另一些边、角的过程,叫做解直角三角形.
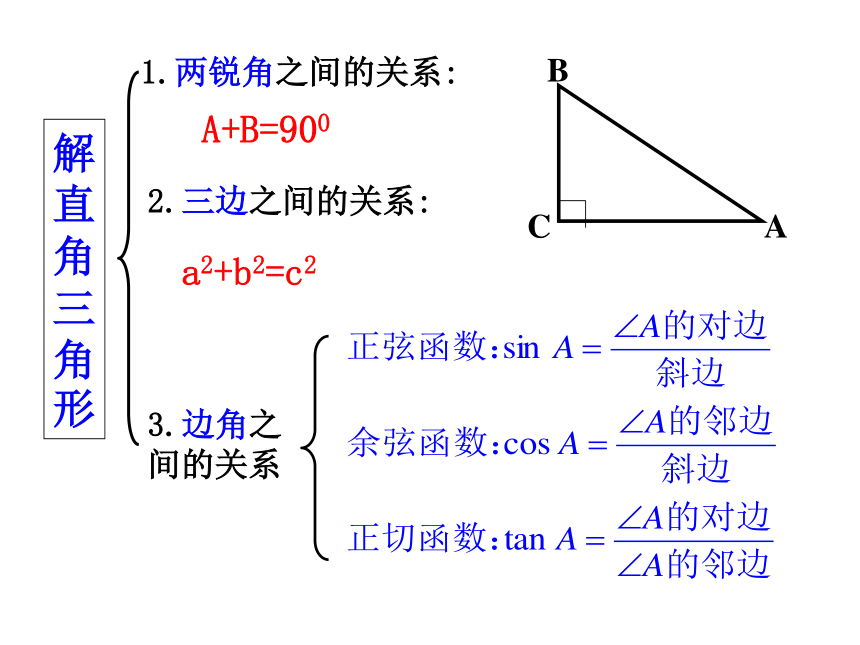
解直角三角形
1.两锐角之间的关系:
2.三边之间的关系:
3.边角之间的关系
A+B=900
a2+b2=c2
C
A
B
例1、如图,在Rt△ABC中,∠C=900,∠A=500,BC=3,求∠B和AB,b(边长保留2个有效数字)
B
C
a=3
b
A
解:Rt△ABC中
∠B=900-∠A=400
∴AB=a÷sinA=3÷sin500≈3.9
∴b=a÷tanA=3÷tan500≈2.5
sin50°≈0.7660,cos50 ° ≈ 0.6428,
tan50 °≈1.1918
解:
在Rt△ABD中,
a= ( )2+(h)2
l
2
= 52+3.52 ≈6.1(m).
h
L
a
A
B
C
D
α
∵tanα= =0.7,
3.5
5
∴α≈350.
答:斜面钢条a的长度约为6.1米,坡角约为350.
例2、如图是某市“平改坡”工程中一种坡屋顶设计,已知平顶屋面的宽度L为10m,坡屋顶的设计高度h为3.5m,能求斜面钢条a的长度和坡角a。(长度精确到0.1米,角度精确到1°)
在解直角三角形的过程中,常会遇到近似计算,本书除特别说明外,边长保留四个有效数字,角度精确到1′.
解直角三角形,只有下面两种情况:
(1)已知两条边;
(2)已知一条边和一个锐角
特别强调:
(必须有一个条件是边)
1、在△ABC中,已知a,b,c分别为∠A,∠B和∠C的对边,∠C=900,根据下列条件解直角三角形(长度保留到2个有效数字,角度精确到1度)
C
A
B
(1)c=10,∠A=30°
(2)b=4,∠B=72°
(3)a=5, c=7
练一练
(4)a=20,sinA=
例如图19.4.1所示,一棵大树在一次强烈的地震中于离地面10米处折断倒下,树顶落在离树根24米处.大树在折断之前高多少?
解 利用勾股定理可以求出折断倒下部分的长度为:
26+10=36(米).
答:大树在折断之前高为36米.
如图东西两炮台A、B相距2000米,同时发现入侵敌舰C,炮台A测得敌舰C在它的南偏东40゜的方向,炮台B测得敌舰C在它的正南方,试求敌舰与两炮台的距离.(精确到1米)
本题是已知
一边,一锐角.
应用练习
解 在Rt△ABC中
∵∠CAB=90゜-∠DAC=50゜
答:敌舰与A、B两炮台的距离分别约为3111米和2384米.
∴BC=AB tan∠CAB
=2000×tan50゜≈2384(米).
∴ =tan∠CAB
在⊿ABC中,∠C=900,
解直角三角形:(如图)
1.已知a,b.解直角三角形(即求:∠A,∠B及C边)
2. 已知∠A,a.解直角三角形
3.已知∠A,b. 解直角三角形
4. 已知∠A,c. 解直角三角形
b
A
B
C
a
┌
c
已知
解直角三角形
a, b
tanA=
a
b
∠A, a
C=
a
sinA
∠A, b
b=
a
tanA
C=
b
cosA
a=b×tanA
C= a2+b2
∠A, C
a=c×sinA
b=c×cosA
解直角三角形中的边角关系
C
B
A
1.已知,在△ABC中,∠B=45°,AC=4,BC=2 , 求sinA和AB的值。
2、已知,在△ABC中,∠B=60°,∠C=45°,BC=5㎝。求AB的长。
A
C
B
4
2
45°
B
A
C
45
60°
45°
三角函数定义
α 30° 45° 60°
sinα
cosα
tanα
特殊角的三角函数值
1、如图,在Rt△ABC中,∠C=90°
(1)若∠A=30°,BC=2,求AC、AB、∠B
A
C
B
(2)若BC=2,AB=4,求AC、∠A、∠B
合作探究
合作探究
2、已知在Rt△ABC中,∠C= Rt∠,AB=5,AC=3,求边BC的长。你能求出∠A的度数么?
3、已知在Rt△ABC中, ∠C= Rt∠ ,∠A=560,AB=8,求AC的长。
sin37°≈0.6,cos53 ° ≈ 0.6,tan30 °≈0.6
sin56°≈0.8290,cos56°≈ 0.5592,tan56°≈1.483
在上述例题中,我们都是利用直角三角形中的已知边、角来求出另外一些的边角.像这样,
********************************
在直角三角形中,由已知的一些边、角,求出另一些边、角的过程,叫做解直角三角形.
解直角三角形
1.两锐角之间的关系:
2.三边之间的关系:
3.边角之间的关系
A+B=900
a2+b2=c2
C
A
B
例1、如图,在Rt△ABC中,∠C=900,∠A=500,BC=3,求∠B和AB,b(边长保留2个有效数字)
B
C
a=3
b
A
解:Rt△ABC中
∠B=900-∠A=400
∴AB=a÷sinA=3÷sin500≈3.9
∴b=a÷tanA=3÷tan500≈2.5
sin50°≈0.7660,cos50 ° ≈ 0.6428,
tan50 °≈1.1918
解:
在Rt△ABD中,
a= ( )2+(h)2
l
2
= 52+3.52 ≈6.1(m).
h
L
a
A
B
C
D
α
∵tanα= =0.7,
3.5
5
∴α≈350.
答:斜面钢条a的长度约为6.1米,坡角约为350.
例2、如图是某市“平改坡”工程中一种坡屋顶设计,已知平顶屋面的宽度L为10m,坡屋顶的设计高度h为3.5m,能求斜面钢条a的长度和坡角a。(长度精确到0.1米,角度精确到1°)
在解直角三角形的过程中,常会遇到近似计算,本书除特别说明外,边长保留四个有效数字,角度精确到1′.
解直角三角形,只有下面两种情况:
(1)已知两条边;
(2)已知一条边和一个锐角
特别强调:
(必须有一个条件是边)
1、在△ABC中,已知a,b,c分别为∠A,∠B和∠C的对边,∠C=900,根据下列条件解直角三角形(长度保留到2个有效数字,角度精确到1度)
C
A
B
(1)c=10,∠A=30°
(2)b=4,∠B=72°
(3)a=5, c=7
练一练
(4)a=20,sinA=
例如图19.4.1所示,一棵大树在一次强烈的地震中于离地面10米处折断倒下,树顶落在离树根24米处.大树在折断之前高多少?
解 利用勾股定理可以求出折断倒下部分的长度为:
26+10=36(米).
答:大树在折断之前高为36米.
如图东西两炮台A、B相距2000米,同时发现入侵敌舰C,炮台A测得敌舰C在它的南偏东40゜的方向,炮台B测得敌舰C在它的正南方,试求敌舰与两炮台的距离.(精确到1米)
本题是已知
一边,一锐角.
应用练习
解 在Rt△ABC中
∵∠CAB=90゜-∠DAC=50゜
答:敌舰与A、B两炮台的距离分别约为3111米和2384米.
∴BC=AB tan∠CAB
=2000×tan50゜≈2384(米).
∴ =tan∠CAB
在⊿ABC中,∠C=900,
解直角三角形:(如图)
1.已知a,b.解直角三角形(即求:∠A,∠B及C边)
2. 已知∠A,a.解直角三角形
3.已知∠A,b. 解直角三角形
4. 已知∠A,c. 解直角三角形
b
A
B
C
a
┌
c
已知
解直角三角形
a, b
tanA=
a
b
∠A, a
C=
a
sinA
∠A, b
b=
a
tanA
C=
b
cosA
a=b×tanA
C= a2+b2
∠A, C
a=c×sinA
b=c×cosA
解直角三角形中的边角关系
C
B
A
1.已知,在△ABC中,∠B=45°,AC=4,BC=2 , 求sinA和AB的值。
2、已知,在△ABC中,∠B=60°,∠C=45°,BC=5㎝。求AB的长。
A
C
B
4
2
45°
B
A
C
45
60°
45°
