平湖市2011年第七单元图形的初步知识试卷
文档属性
| 名称 | 平湖市2011年第七单元图形的初步知识试卷 |  | |
| 格式 | zip | ||
| 文件大小 | 62.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-12-07 21:06:30 | ||
图片预览



文档简介
平湖市七(上)第七单元试卷
学校 班级 学号 姓名
一、选择题(30分)
1.下列球类实物不属于球体的是( )
(A)足球 (B)篮球 (C)羽毛球 (D)铅球
2.把一条弯曲的河道改成直道,可以缩短航程,其中的道理可以解释为( )
(A)线段有两个端点 (B)过两点可以确定一条直线
(C)两点之间,线段最短 (D)线段可以比较大小
3.下列关于作图的语句中正确的是( )
(A)画直线AB=10厘米 (B)画射线OB=10厘米
(C)已知A、B、C三点,过这三点画一条直线
(D)过直线AB外一点画一条直线和直线AB平行
4.已知:∠A=48°48′、∠B=48.48°、∠C=48°28′48″那么下列各式正确的是( )
(A)∠A>∠B>∠C (B)∠A>∠B =∠C
(C) ∠A>∠C>∠B (C)∠B>∠A>∠C
5.已知∠AOB与其内任意一点P,若过点P画一条直线与OA平行,那么这样的直线( )
(A)有且只有一条 (B)有两条 (C)有无数条 (D)不存在
6.下列说法正确的是( )
(A)没有交点的两条线段互相平行;
(B)在同一平面内,没有交点的两条射线互相平行;
(C)没有交点的一条线段和一条射线互相平行;
(D)互相平行的两条直线没有交点。
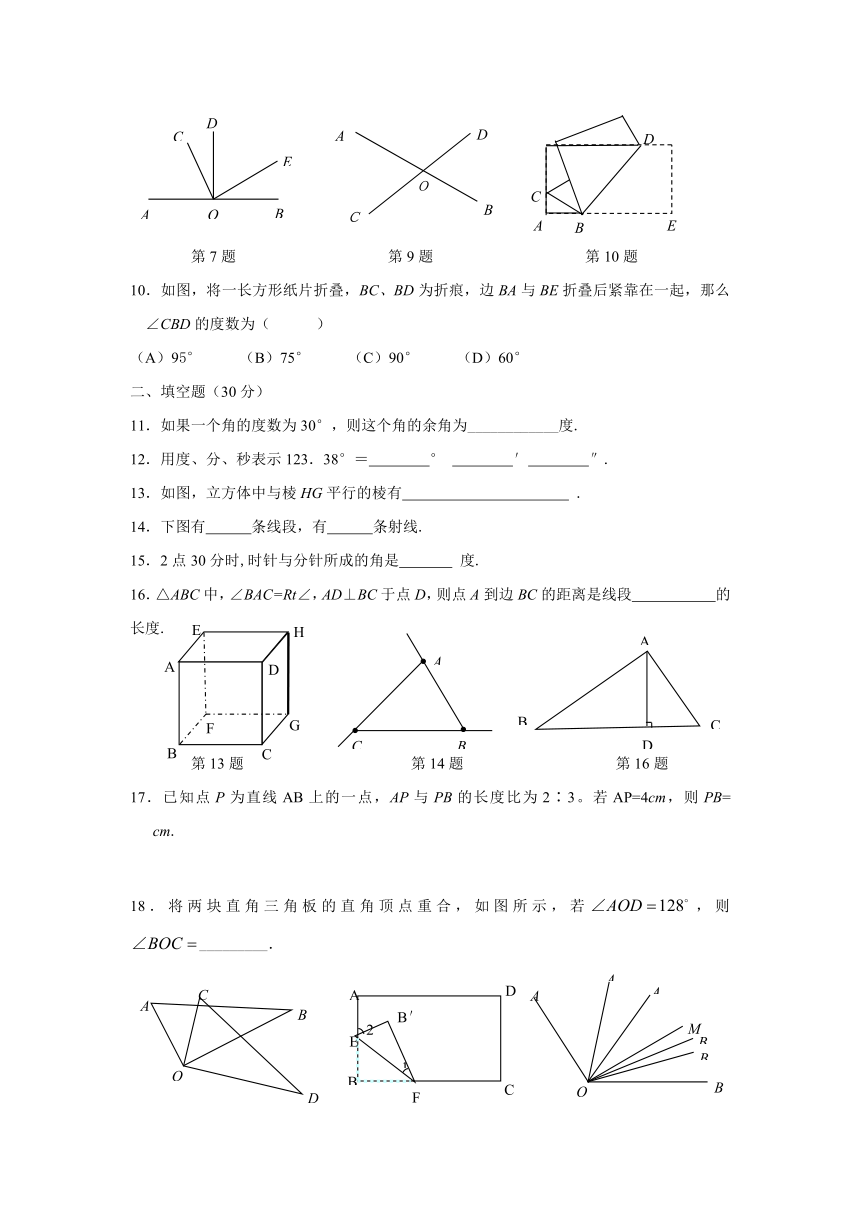
7.如图,∠AOD=∠DOB=∠COE=90 ,除直角外其余相等的角有 ( )
(A)2对 (B)3对 (C)4对 (D)6对
8.任意画3条直线,则交点的个数是 ( )
(A)1个 (B)1个或3个 (C)1个或2个或3个 (D)0个或1个或2个或3个
9. 如图,直线AB与CD相交于点O,∠AOD+∠BOC=240°,则∠AOC的度数为 ( )
(A)70° (B)60° (C)120° (D)140°
第7题 第9题 第10题
10.如图,将一长方形纸片折叠,BC、BD为折痕,边BA与BE折叠后紧靠在一起,那么∠CBD的度数为( )
(A)95° (B)75° (C)90° (D)60°
二、填空题(30分)
11.如果一个角的度数为30°,则这个角的余角为____________度.
12.用度、分、秒表示123.38°= ° ′ ″.
13.如图,立方体中与棱HG平行的棱有 .
14.下图有 条线段,有 条射线.
15.2点30分时,时针与分针所成的角是 度.
16.△ABC中,∠BAC=Rt∠,AD⊥BC于点D,则点A到边BC的距离是线段 的长度.
第13题 第14题 第16题
17.已知点P为直线AB上的一点,AP与PB的长度比为2∶3。若AP=4cm,则PB= cm.
18.将两块直角三角板的直角顶点重合,如图所示,若,则_________.
第18题 第19题 第20题
19.如图,把长方形纸片一角沿EF折叠,使点B落在B′处,已知∠1=35°;则
∠2= .
20.如图∠AOB=α°,OA1、OB1分别是∠AOM和∠MOB的平分线,OA2、OB2分别是∠A1OM和∠MOB1的平分线, OA3、OB3分别是∠A2OM和∠MOB2的平分线,…OAn、OBn分别是∠An-1OM和∠MOBn-1的平分线,则∠AnOBn= °.
三、简答题(40分)
21.如图,A、B分别是公路l旁的两个村庄;
(1)如图1,A、B在公路两侧时,在公路上找到一点C作为车站,使它到两村庄的距离和最近,请在图1上表示出来.
(2)如图2,能否找到一点C作为车站,使它到村庄A的距离最近,如果能请在图2上作出点C.
22.一个角的补角是这个角的余角的3倍,求这个角的度数.
23.如图,O是直线AB上的一点,OM是∠AOC的角平分线,ON是∠BOC的角平分线,
(1)图中互补的角有哪几对.
(2)已知∠AOM=20°,求∠CON的度数.
24.如图,D、B、E是线段AC上的三点,且AD=DB,E是BC的中点,BE=AC=2cm,求线段DE的长.
四、附加题(10分)
25.如图所示,
(1)在∠AOB中,以O为顶点引射线, 填下表:
∠AOB内射线条数 1 2 3 4 …
角的总个数
(2)若∠AOB内射线的条数是n,你能用n的式子表示上面的结论吗?如果能请表示出来.
(3)若根据(2)的结论,当n=2011时,共有几个角?
参考答案
一、(1)——(5) CCDBA (6)——(10) DADBC
二、(11)60° (12)123°22′48″ (13)AB,DC,EF (14)3,6 (15)105 (16)AD
(17)6cm或2cm(18)52° (19)70° (20)α°
三、(21)略(22)45°(23)5对,∠AOM+∠MOB=180°,∠COM+∠MOB=180,∠AOC+∠COB=180,∠AON+∠NOB=180,∠CON+∠AON=180,70°(24)∵BE=AC=2 cm ∴AC=10 cm 又∵E是BC的中点 ∴EC=BE=2 cm ∴AB=AC-BC=6 cm 又∵AD=DB ∴AD=2 cm DB=4 cm ∴DE=BD+BE=6 cm
四、附加题(25)(1) 3 ,6,10,15 (2) (3)
七年级上册图形的初步知识细目表
题号 分值 知识点 技能目标 难易程度 难度系数 估分
了解 理解 掌握 易 中 难
1 3 几何体与立体图形 √ √ 1 3
2 3 两点之间线段最短的应用 √ √ 0.95 2.8
3 3 直线、射线和线段的性质 √ √ 0.85 2.5
4 3 角的大小的比较 √ √ 0.8 2.4
5 3 过直线外一点,有且仅有一条直线平行于已知直线 √ √ 0.9 2.7
6 3 进一步认识线段、射线、直线和平行线的有关概念 √ √ 0.7 2.1
7 3 同角的余角相等的应用 √ √ 0.8 2.4
8 3 相交线的有关知识 √ √ 0.8 2.4
9 3 对顶角、补角等在解决问题中的一些应用 √ √ 0.9 2.7
10 3 角平分线的实际应用 √ √ 0.7 2.1
11 3 余角的计算 √ √ 0.9 2.7
12 3 度、分、秒单位及其换算 √ √ 0.8 2.4
13 3 平行线的简单实际应用 √ √ 0.8 2.4
14 3 进一步认识线段、射线的有关概念 √ √ 0.8 2.4
15 3 角等在解决问题中的一些应用 √ √ 0.8 2.4
16 3 直线外一点与直线上个点连接的所有线段中,垂线段最短 √ √ 0.8 2.4
17 3 线段的和差和分类讨论的数学思想 √ √ 0.7 2.1
18 3 角度大小的综合应用 √ √ 0.7 2.1
19 3 角平分线、补角等在解决问题中的一些应用 √ √ 0.7 2.1
20 3 角平分的应用 √ √ 0.65 2
21 10 作图,两点间线段最短及点到直线的距离最短的应用 √ √ 0.9 9
22 10 补角和余角 √ √ 0.8 8
23 10 角平分线、互补角的应用及有关角的一些计算 √ √ 0.7 7
24 10 线段的有关计算 √ √ 0.7 7
25 10 会结合角的概念进行角的计数,初步学会规律性问题的一般探究方法 √ √ 0.5 5
79.1
出题思路:
本章重点知识为:线段和角的基本知识和一些基本计算。“两点间线段最短”和“过两点确定一条直线”;“过一点作垂线和过一点作平行线”;“垂线段最短”、“对顶角相等”等知识的基本应用、会基本的作图:作线段的和差、过一点会作已知直线的平行线和垂线段。
经过本小组老师的商量和讨论,整章试卷力求知识点全面,重点明确,检测一些平时要求掌握的知识,为以后的几何学习打下基础,让学生初步体会几何的逻辑推理。
第2题:是书本P160页,小狗吃骨头的不同路线的情景的改编题,主要目的是为了能初步的进行“两点线段最短”的说理应用。
第3题:是学习第二节课《线段、射线、直线》及画《平行线》后的实践操作,是“两点确定一直线及过直线外一点画平行线”的理解及表述,也是学习如何正确表述基本几何语言及培养几何语言的要求。
第4题:综合考查了角度的“度、分、秒”的转化。
第5题:改编自P181页的13题。点P是∠ABC内一点,(1)过点P画一条直线平行于BC;(2)过点P画一条直线垂直于AB。
第6题:考查平行线的定义。
第7题:改编自P169页“做一做”中的第2题及例1,两题结合在一起,组合而成。主要是想考查学生互余角的两种数法:(1)找本身是直角,然后被其中一条线分成两个角的。通过等量代换,寻找其他互余的角。(2)找在直角三角形中存在着的互余的角。
“做一做”(2)如图,点O为直线AB上一点,∠AOC=Rt∠,OD是∠BOC内的一条射线,图中有哪些角互补?有哪些角互余?说明你的理由。
例1:已知∠AOC=∠BOD= Rt∠,指出图中还有哪些角相等,并说明理由。
做一做2 例1
第8题:改编自P156页作业题(5)。考查直线与直线关系知识的全面理解。
第9题:考查对顶角及互补的知识。
第10题:改编自P173的材料操作。考查动手操作能力及角平分线的实际应用。
如图,把这张纸展开后,折痕AB与CD相交于点O,则∠AOC,∠AOD,∠BOC,∠BOD与∠1有什么关系?它们都是什么角?
第11题:考查互余的定义。(原创题)
第13题:改编自P161页:已知点P为线段AB上的一点,AP与PB的长度比为2:3。若AP=4,求PB,AB的长。原题一解,现为两解。体现数学的严谨性。
已知点P为直线AB上的一点,AP与PB的长度比为2:3。若AP=4,则PB= 。
因为缺少垂线段最短的应用,及平行线的了解,所以我们讨论后加了第16题和第17题,是我们当时在讨论时编的简单题。
16.△ABC中,∠BAC=Rt∠,AD⊥BC于点D,则点A到边BC的距离是线段 的长度.
第16题 第17题
17.如图,立方体中与棱HG平行的棱有 .
第18题:角度大小的实际应用,重叠问题。
第19题:折纸问题:如何求角度的大小,涉及直角三角形两锐角的关系及角的互补关系。
第20题:(原创题)目的是想通过角平线知识来让学生学会找规律。
第21题:改编自P161作业题6:四个村庄A、B、C、D准备合打一口井,在什么位置时到四村的距离和最小。和P181页的13题。点P是∠ABC内一点,(1)过点P画一条直线平行于BC;(2)过点P画一条直线垂直于AB。
第22题:改编自P169例2:已知一个角的补角是这个角的余角的4倍,求这个角的度数。
第23题:考查互补和角平分线的综合应用。
第24题:(原创题)根据线段中点及之间关系,进行计算。
第25题:体现一种归纳的数学思想:让学生从特殊中发现普遍规律,抓住问题的本质,学会分析题目的方法。
O
C
D
B
A
A
B
C
D
E
A
B
C
E
D
O
A
B
D
C
A
C
B
A
B
C
D
G
H
E
F
O
A
A1
M
B
B1
A2
B2
A
B
O
D
C
2
1
D
C
F
E
B
A
B′
A
B
l
图2
A
B
l
图1
N
C
O
B
A
M
A
D
B
E
C
O
A
B
C
A
B
O
C
D
P
C
B
A
A
O
D
C
B
O
D
C
B
A
O
A
B
D
C
1
A
B
C
D
G
H
E
F
A
B
D
C
P
C
B
A
学校 班级 学号 姓名
一、选择题(30分)
1.下列球类实物不属于球体的是( )
(A)足球 (B)篮球 (C)羽毛球 (D)铅球
2.把一条弯曲的河道改成直道,可以缩短航程,其中的道理可以解释为( )
(A)线段有两个端点 (B)过两点可以确定一条直线
(C)两点之间,线段最短 (D)线段可以比较大小
3.下列关于作图的语句中正确的是( )
(A)画直线AB=10厘米 (B)画射线OB=10厘米
(C)已知A、B、C三点,过这三点画一条直线
(D)过直线AB外一点画一条直线和直线AB平行
4.已知:∠A=48°48′、∠B=48.48°、∠C=48°28′48″那么下列各式正确的是( )
(A)∠A>∠B>∠C (B)∠A>∠B =∠C
(C) ∠A>∠C>∠B (C)∠B>∠A>∠C
5.已知∠AOB与其内任意一点P,若过点P画一条直线与OA平行,那么这样的直线( )
(A)有且只有一条 (B)有两条 (C)有无数条 (D)不存在
6.下列说法正确的是( )
(A)没有交点的两条线段互相平行;
(B)在同一平面内,没有交点的两条射线互相平行;
(C)没有交点的一条线段和一条射线互相平行;
(D)互相平行的两条直线没有交点。
7.如图,∠AOD=∠DOB=∠COE=90 ,除直角外其余相等的角有 ( )
(A)2对 (B)3对 (C)4对 (D)6对
8.任意画3条直线,则交点的个数是 ( )
(A)1个 (B)1个或3个 (C)1个或2个或3个 (D)0个或1个或2个或3个
9. 如图,直线AB与CD相交于点O,∠AOD+∠BOC=240°,则∠AOC的度数为 ( )
(A)70° (B)60° (C)120° (D)140°
第7题 第9题 第10题
10.如图,将一长方形纸片折叠,BC、BD为折痕,边BA与BE折叠后紧靠在一起,那么∠CBD的度数为( )
(A)95° (B)75° (C)90° (D)60°
二、填空题(30分)
11.如果一个角的度数为30°,则这个角的余角为____________度.
12.用度、分、秒表示123.38°= ° ′ ″.
13.如图,立方体中与棱HG平行的棱有 .
14.下图有 条线段,有 条射线.
15.2点30分时,时针与分针所成的角是 度.
16.△ABC中,∠BAC=Rt∠,AD⊥BC于点D,则点A到边BC的距离是线段 的长度.
第13题 第14题 第16题
17.已知点P为直线AB上的一点,AP与PB的长度比为2∶3。若AP=4cm,则PB= cm.
18.将两块直角三角板的直角顶点重合,如图所示,若,则_________.
第18题 第19题 第20题
19.如图,把长方形纸片一角沿EF折叠,使点B落在B′处,已知∠1=35°;则
∠2= .
20.如图∠AOB=α°,OA1、OB1分别是∠AOM和∠MOB的平分线,OA2、OB2分别是∠A1OM和∠MOB1的平分线, OA3、OB3分别是∠A2OM和∠MOB2的平分线,…OAn、OBn分别是∠An-1OM和∠MOBn-1的平分线,则∠AnOBn= °.
三、简答题(40分)
21.如图,A、B分别是公路l旁的两个村庄;
(1)如图1,A、B在公路两侧时,在公路上找到一点C作为车站,使它到两村庄的距离和最近,请在图1上表示出来.
(2)如图2,能否找到一点C作为车站,使它到村庄A的距离最近,如果能请在图2上作出点C.
22.一个角的补角是这个角的余角的3倍,求这个角的度数.
23.如图,O是直线AB上的一点,OM是∠AOC的角平分线,ON是∠BOC的角平分线,
(1)图中互补的角有哪几对.
(2)已知∠AOM=20°,求∠CON的度数.
24.如图,D、B、E是线段AC上的三点,且AD=DB,E是BC的中点,BE=AC=2cm,求线段DE的长.
四、附加题(10分)
25.如图所示,
(1)在∠AOB中,以O为顶点引射线, 填下表:
∠AOB内射线条数 1 2 3 4 …
角的总个数
(2)若∠AOB内射线的条数是n,你能用n的式子表示上面的结论吗?如果能请表示出来.
(3)若根据(2)的结论,当n=2011时,共有几个角?
参考答案
一、(1)——(5) CCDBA (6)——(10) DADBC
二、(11)60° (12)123°22′48″ (13)AB,DC,EF (14)3,6 (15)105 (16)AD
(17)6cm或2cm(18)52° (19)70° (20)α°
三、(21)略(22)45°(23)5对,∠AOM+∠MOB=180°,∠COM+∠MOB=180,∠AOC+∠COB=180,∠AON+∠NOB=180,∠CON+∠AON=180,70°(24)∵BE=AC=2 cm ∴AC=10 cm 又∵E是BC的中点 ∴EC=BE=2 cm ∴AB=AC-BC=6 cm 又∵AD=DB ∴AD=2 cm DB=4 cm ∴DE=BD+BE=6 cm
四、附加题(25)(1) 3 ,6,10,15 (2) (3)
七年级上册图形的初步知识细目表
题号 分值 知识点 技能目标 难易程度 难度系数 估分
了解 理解 掌握 易 中 难
1 3 几何体与立体图形 √ √ 1 3
2 3 两点之间线段最短的应用 √ √ 0.95 2.8
3 3 直线、射线和线段的性质 √ √ 0.85 2.5
4 3 角的大小的比较 √ √ 0.8 2.4
5 3 过直线外一点,有且仅有一条直线平行于已知直线 √ √ 0.9 2.7
6 3 进一步认识线段、射线、直线和平行线的有关概念 √ √ 0.7 2.1
7 3 同角的余角相等的应用 √ √ 0.8 2.4
8 3 相交线的有关知识 √ √ 0.8 2.4
9 3 对顶角、补角等在解决问题中的一些应用 √ √ 0.9 2.7
10 3 角平分线的实际应用 √ √ 0.7 2.1
11 3 余角的计算 √ √ 0.9 2.7
12 3 度、分、秒单位及其换算 √ √ 0.8 2.4
13 3 平行线的简单实际应用 √ √ 0.8 2.4
14 3 进一步认识线段、射线的有关概念 √ √ 0.8 2.4
15 3 角等在解决问题中的一些应用 √ √ 0.8 2.4
16 3 直线外一点与直线上个点连接的所有线段中,垂线段最短 √ √ 0.8 2.4
17 3 线段的和差和分类讨论的数学思想 √ √ 0.7 2.1
18 3 角度大小的综合应用 √ √ 0.7 2.1
19 3 角平分线、补角等在解决问题中的一些应用 √ √ 0.7 2.1
20 3 角平分的应用 √ √ 0.65 2
21 10 作图,两点间线段最短及点到直线的距离最短的应用 √ √ 0.9 9
22 10 补角和余角 √ √ 0.8 8
23 10 角平分线、互补角的应用及有关角的一些计算 √ √ 0.7 7
24 10 线段的有关计算 √ √ 0.7 7
25 10 会结合角的概念进行角的计数,初步学会规律性问题的一般探究方法 √ √ 0.5 5
79.1
出题思路:
本章重点知识为:线段和角的基本知识和一些基本计算。“两点间线段最短”和“过两点确定一条直线”;“过一点作垂线和过一点作平行线”;“垂线段最短”、“对顶角相等”等知识的基本应用、会基本的作图:作线段的和差、过一点会作已知直线的平行线和垂线段。
经过本小组老师的商量和讨论,整章试卷力求知识点全面,重点明确,检测一些平时要求掌握的知识,为以后的几何学习打下基础,让学生初步体会几何的逻辑推理。
第2题:是书本P160页,小狗吃骨头的不同路线的情景的改编题,主要目的是为了能初步的进行“两点线段最短”的说理应用。
第3题:是学习第二节课《线段、射线、直线》及画《平行线》后的实践操作,是“两点确定一直线及过直线外一点画平行线”的理解及表述,也是学习如何正确表述基本几何语言及培养几何语言的要求。
第4题:综合考查了角度的“度、分、秒”的转化。
第5题:改编自P181页的13题。点P是∠ABC内一点,(1)过点P画一条直线平行于BC;(2)过点P画一条直线垂直于AB。
第6题:考查平行线的定义。
第7题:改编自P169页“做一做”中的第2题及例1,两题结合在一起,组合而成。主要是想考查学生互余角的两种数法:(1)找本身是直角,然后被其中一条线分成两个角的。通过等量代换,寻找其他互余的角。(2)找在直角三角形中存在着的互余的角。
“做一做”(2)如图,点O为直线AB上一点,∠AOC=Rt∠,OD是∠BOC内的一条射线,图中有哪些角互补?有哪些角互余?说明你的理由。
例1:已知∠AOC=∠BOD= Rt∠,指出图中还有哪些角相等,并说明理由。
做一做2 例1
第8题:改编自P156页作业题(5)。考查直线与直线关系知识的全面理解。
第9题:考查对顶角及互补的知识。
第10题:改编自P173的材料操作。考查动手操作能力及角平分线的实际应用。
如图,把这张纸展开后,折痕AB与CD相交于点O,则∠AOC,∠AOD,∠BOC,∠BOD与∠1有什么关系?它们都是什么角?
第11题:考查互余的定义。(原创题)
第13题:改编自P161页:已知点P为线段AB上的一点,AP与PB的长度比为2:3。若AP=4,求PB,AB的长。原题一解,现为两解。体现数学的严谨性。
已知点P为直线AB上的一点,AP与PB的长度比为2:3。若AP=4,则PB= 。
因为缺少垂线段最短的应用,及平行线的了解,所以我们讨论后加了第16题和第17题,是我们当时在讨论时编的简单题。
16.△ABC中,∠BAC=Rt∠,AD⊥BC于点D,则点A到边BC的距离是线段 的长度.
第16题 第17题
17.如图,立方体中与棱HG平行的棱有 .
第18题:角度大小的实际应用,重叠问题。
第19题:折纸问题:如何求角度的大小,涉及直角三角形两锐角的关系及角的互补关系。
第20题:(原创题)目的是想通过角平线知识来让学生学会找规律。
第21题:改编自P161作业题6:四个村庄A、B、C、D准备合打一口井,在什么位置时到四村的距离和最小。和P181页的13题。点P是∠ABC内一点,(1)过点P画一条直线平行于BC;(2)过点P画一条直线垂直于AB。
第22题:改编自P169例2:已知一个角的补角是这个角的余角的4倍,求这个角的度数。
第23题:考查互补和角平分线的综合应用。
第24题:(原创题)根据线段中点及之间关系,进行计算。
第25题:体现一种归纳的数学思想:让学生从特殊中发现普遍规律,抓住问题的本质,学会分析题目的方法。
O
C
D
B
A
A
B
C
D
E
A
B
C
E
D
O
A
B
D
C
A
C
B
A
B
C
D
G
H
E
F
O
A
A1
M
B
B1
A2
B2
A
B
O
D
C
2
1
D
C
F
E
B
A
B′
A
B
l
图2
A
B
l
图1
N
C
O
B
A
M
A
D
B
E
C
O
A
B
C
A
B
O
C
D
P
C
B
A
A
O
D
C
B
O
D
C
B
A
O
A
B
D
C
1
A
B
C
D
G
H
E
F
A
B
D
C
P
C
B
A
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
