浙教版九年级上册第四章 《相似三角形》单元评价B卷(Word版 附答案)
文档属性
| 名称 | 浙教版九年级上册第四章 《相似三角形》单元评价B卷(Word版 附答案) |  | |
| 格式 | zip | ||
| 文件大小 | 810.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-28 15:19:40 | ||
图片预览


文档简介
浙教版九年级上册第四章
《相似三角形》单元评价B卷
班级:
_________
姓名:
_________
得分:
_________
一、选择题(每小题3分,共30分)
1.下列命题中,是真命题的为(
)
A.锐角三角形都相似
B.直角三角形都相似
C.等腰三角形都相似
D.等边三角形都相似
2.在平行四边形ABCD中,O1,O2,O3为对角线BD上三点,且BO1
=
O1O2
=
O2,O3,3
=
O3,D,连结AO1,并延长交BC于点E,连结EO3并延长交AD于点F,则AD:FD等于(
)
A.19:2
B.9:1
C.8:11
D.7:1
3.如图,P是Rt△ABC的斜边BC上异于B,C的一点,过点P作直线截△ABC,使截得的三角形与△ABC相似,满足这样条件的直线共有(
)
A.1条
B.2条
C.3条
D.4条
4.如图,已知AD为△ABC的角平分线,DE∥AB交AC于点E,如果
=
,那么
=
( )
A.
B.
C.
D.
5.如图,E,G,F,H分别是矩形ABCD四条边上的点,EF⊥GH,若AB
=
2,BC
=
3,则EF:GH(
)
A.2:3
B.3:2
C.4:9
D.无法确定
6.将△ABC的高AD三等分,过每一个分点作底边的平行线,把三角形分成三部分,设这三部分的面积为S1,S2,S3,则S1:S2:S3为(
)
A.1:2:3
B.2:3:4
C.1:3:5
D.3:5:7
7.已知△ABC的三边长分别为20
cm,50
cm,60
cm,现要利用长度分别为30
cm和60
cm的细木条各一根,做一个三角形木架与三角形相似,要求以其中一根为一边,将另一根截成两段(允许有余料)作为另外两边.那么另两边的长度(单位:cm)分别为(
)
A.10,25
B.10,36或12,36
C.12,36
D.10,25或12,36
8.如图,Rt△ABC中,∠ACB
=
90°,∠ABC
=
60°,BC
=
2
cm,D为BC的中点,若动点E以1
cm/s的速度从A点出发,沿着A→B→A的方向运动,设E点的运动时间为t秒(0
≤
t
<
6),连接DE,当△BDE是直角三角形时,t的值为(
)
A.2
B.2.5或3.5
C.3.5或4.5
D.2或3.5或4.5
9.如图,在正方形网格中,每个小正方形的边长均相等,网格中三个多边形(分别标记为①,②,③)的顶点均在格点上.被一个多边形覆盖的网格线中,竖直部分线段长度之和记为m,水平部分线段长度之和记为n,则这三个多边形中满足m=n的是(
)
A.只有②
B.只有③
C.②③
D.①②③
10.如图,∠BAC
=
∠DAF
=
90°,AB
=
AC,AD
=
AF,点D、E为BC边上的两点,且∠DAE
=
45°,连接EF、BF,则下列结论:
①△AED≌△AEF;②△ABE∽△ACD;③BE
+
DC
>
DE;④BE
2
+
DC
2
=
DE
3,
其中正确的有( )个.
A.1
B.2
C.3
D.4
二、填空题(每小题4分,共24分)
11.如图,点D、E分别为△ABC的边AB、AC上的中点,则△ADE的面积与四边形BCED的面积的比为
_________
.
12.如图,两个多边形若相似,则x只能取
_________
.
13.如图,小明用长为3
m的竹竿CD做测量工具,测量学校旗杆AB的高度,移动竹竿,使竹竿与旗杆的距离DB
=
12
m,则旗杆AB的高为
_________
m.
14.如图,在直角坐标系中,有两个点A(4,0),B(0,2),如果点C在x轴上(点C与点A
不重合),当点C坐标为
_________
时,使得由B,O,C三点组成的三角形和△AOB相似.
15.如图,在△ABC中,中线BE,CD相交于点O,连接DE,下列结论:
①
=
;②
=
;③
=
;④
=
其中正确的序号是
_________
.
16.如图,在直角梯形ABCD中,∠BCD
=
90°,AD∥BC,BC
=
CD,E为梯形内一点,且∠BEC
=
90°,将△BEC绕C点旋转90°使BC与DC重合,得到△DCF,连结EF交CD于点M.已知BC
=
5,CF
=
3,则DM:MC的值为
_________
.
三、解答题(共66分)
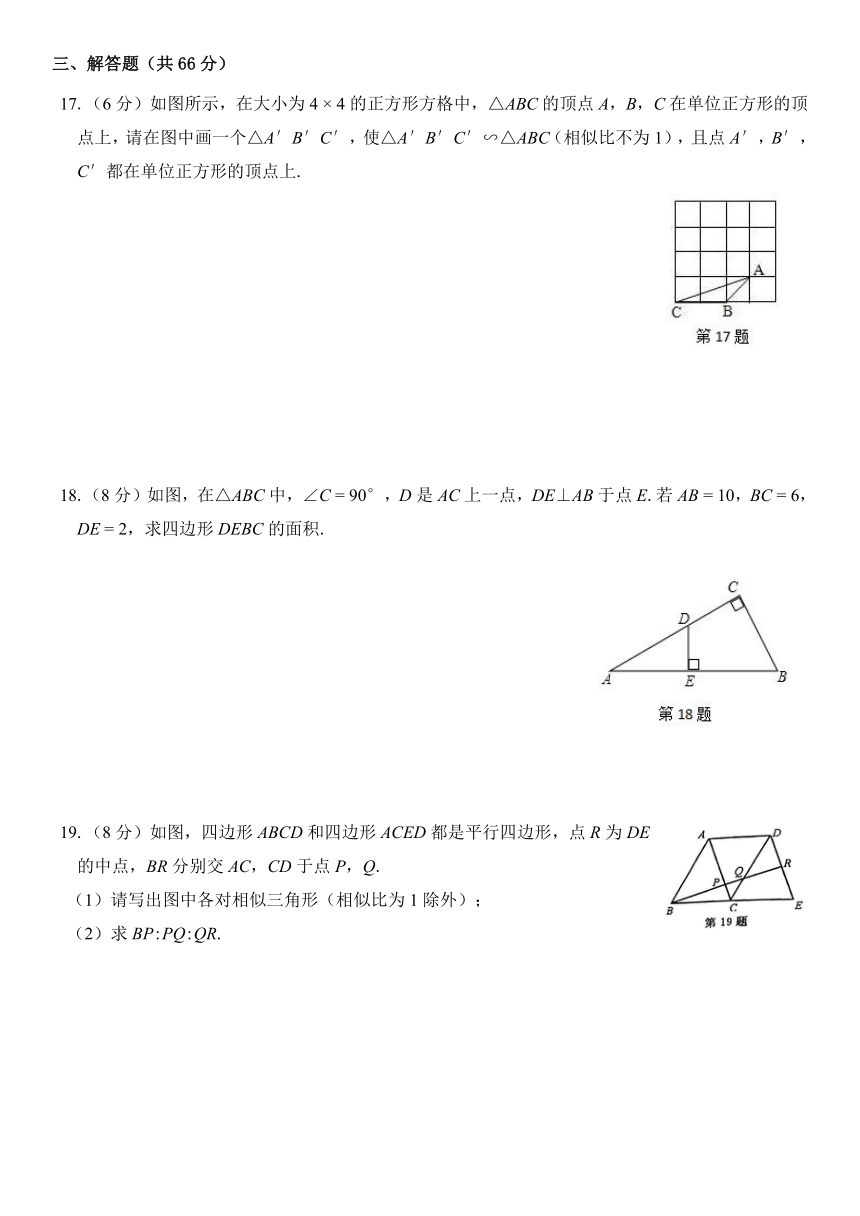
17.(6分)如图所示,在大小为4
×
4的正方形方格中,△ABC的顶点A,B,C在单位正方形的顶点上,请在图中画一个△A′B′C′,使△A′B′C′∽△ABC(相似比不为1),且点A′,B′,C′都在单位正方形的顶点上.
18.(8分)如图,在△ABC中,∠C
=
90°,D是AC上一点,DE⊥AB于点E.若AB
=
10,BC
=
6,DE
=
2,求四边形DEBC的面积.
19.(8分)如图,四边形ABCD和四边形ACED都是平行四边形,点R为DE的中点,BR分别交AC,CD于点P,Q.
(1)请写出图中各对相似三角形(相似比为1除外);
(2)求BP:PQ:QR.
20.(10分)如图,△ABC是一张锐角三角形的硬纸片,AD是边BC上的高,BC
=
40
cm,AD
=
30
cm,从这张硬纸片上剪下一个长HG是宽HE的2倍的矩形EFGH,使它的一边EF在BC上,顶点G,H分别在AC,AB上,AD与HG的交点为M.
(1)求证:
=
;
(2)求这个矩形EFGH的周长.
21.(10分)△ABC中,D是BC上一点,若
=
,则称AD为△ABC的黄金分割线.
(1)求证:若AD为△ABC的黄金分割线,则D是BC的黄金分割点;
(2)若S△ABC
=
20,求△ACD的面积.(结果保留根号)
22.(12分)如图,矩形ABCD的四个顶点A,B,C,D均在正方形网格(网格中正方形的边长为1)的格点(即小正方形的顶点)上.
(1)若AB
=
5,BC
=
2,试在AB边上找点E,使得CE,DE分矩形ABCD所成的三个三角形都相似,请你通过计算找到点E的位置;
(2)若AB
=
5,BC
=
3,能否在AB边上找点E,使得CE,DE分矩形ABCD所成的三个三角形都相似!
请说明你的理由.
23.(12分)如图,在Rt△ABC中,∠ACB
=
90°,AC
=
6
cm,BC
=
8
cm,动点P从点B出发,在BA边上以每秒5
cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4
cm的速度向点B匀速运动,运动时间为t
s(0
<
t
<
2),连结PQ.
(1)若△BPQ与△ABC相似,求t的值;
(2)连结AQ,CP,若AQ⊥CP,求t的值.
《相似三角形》单元评价B卷
班级:
_________
姓名:
_________
得分:
_________
一、选择题(每小题3分,共30分)
1.下列命题中,是真命题的为(
)
A.锐角三角形都相似
B.直角三角形都相似
C.等腰三角形都相似
D.等边三角形都相似
2.在平行四边形ABCD中,O1,O2,O3为对角线BD上三点,且BO1
=
O1O2
=
O2,O3,3
=
O3,D,连结AO1,并延长交BC于点E,连结EO3并延长交AD于点F,则AD:FD等于(
)
A.19:2
B.9:1
C.8:11
D.7:1
3.如图,P是Rt△ABC的斜边BC上异于B,C的一点,过点P作直线截△ABC,使截得的三角形与△ABC相似,满足这样条件的直线共有(
)
A.1条
B.2条
C.3条
D.4条
4.如图,已知AD为△ABC的角平分线,DE∥AB交AC于点E,如果
=
,那么
=
( )
A.
B.
C.
D.
5.如图,E,G,F,H分别是矩形ABCD四条边上的点,EF⊥GH,若AB
=
2,BC
=
3,则EF:GH(
)
A.2:3
B.3:2
C.4:9
D.无法确定
6.将△ABC的高AD三等分,过每一个分点作底边的平行线,把三角形分成三部分,设这三部分的面积为S1,S2,S3,则S1:S2:S3为(
)
A.1:2:3
B.2:3:4
C.1:3:5
D.3:5:7
7.已知△ABC的三边长分别为20
cm,50
cm,60
cm,现要利用长度分别为30
cm和60
cm的细木条各一根,做一个三角形木架与三角形相似,要求以其中一根为一边,将另一根截成两段(允许有余料)作为另外两边.那么另两边的长度(单位:cm)分别为(
)
A.10,25
B.10,36或12,36
C.12,36
D.10,25或12,36
8.如图,Rt△ABC中,∠ACB
=
90°,∠ABC
=
60°,BC
=
2
cm,D为BC的中点,若动点E以1
cm/s的速度从A点出发,沿着A→B→A的方向运动,设E点的运动时间为t秒(0
≤
t
<
6),连接DE,当△BDE是直角三角形时,t的值为(
)
A.2
B.2.5或3.5
C.3.5或4.5
D.2或3.5或4.5
9.如图,在正方形网格中,每个小正方形的边长均相等,网格中三个多边形(分别标记为①,②,③)的顶点均在格点上.被一个多边形覆盖的网格线中,竖直部分线段长度之和记为m,水平部分线段长度之和记为n,则这三个多边形中满足m=n的是(
)
A.只有②
B.只有③
C.②③
D.①②③
10.如图,∠BAC
=
∠DAF
=
90°,AB
=
AC,AD
=
AF,点D、E为BC边上的两点,且∠DAE
=
45°,连接EF、BF,则下列结论:
①△AED≌△AEF;②△ABE∽△ACD;③BE
+
DC
>
DE;④BE
2
+
DC
2
=
DE
3,
其中正确的有( )个.
A.1
B.2
C.3
D.4
二、填空题(每小题4分,共24分)
11.如图,点D、E分别为△ABC的边AB、AC上的中点,则△ADE的面积与四边形BCED的面积的比为
_________
.
12.如图,两个多边形若相似,则x只能取
_________
.
13.如图,小明用长为3
m的竹竿CD做测量工具,测量学校旗杆AB的高度,移动竹竿,使竹竿与旗杆的距离DB
=
12
m,则旗杆AB的高为
_________
m.
14.如图,在直角坐标系中,有两个点A(4,0),B(0,2),如果点C在x轴上(点C与点A
不重合),当点C坐标为
_________
时,使得由B,O,C三点组成的三角形和△AOB相似.
15.如图,在△ABC中,中线BE,CD相交于点O,连接DE,下列结论:
①
=
;②
=
;③
=
;④
=
其中正确的序号是
_________
.
16.如图,在直角梯形ABCD中,∠BCD
=
90°,AD∥BC,BC
=
CD,E为梯形内一点,且∠BEC
=
90°,将△BEC绕C点旋转90°使BC与DC重合,得到△DCF,连结EF交CD于点M.已知BC
=
5,CF
=
3,则DM:MC的值为
_________
.
三、解答题(共66分)
17.(6分)如图所示,在大小为4
×
4的正方形方格中,△ABC的顶点A,B,C在单位正方形的顶点上,请在图中画一个△A′B′C′,使△A′B′C′∽△ABC(相似比不为1),且点A′,B′,C′都在单位正方形的顶点上.
18.(8分)如图,在△ABC中,∠C
=
90°,D是AC上一点,DE⊥AB于点E.若AB
=
10,BC
=
6,DE
=
2,求四边形DEBC的面积.
19.(8分)如图,四边形ABCD和四边形ACED都是平行四边形,点R为DE的中点,BR分别交AC,CD于点P,Q.
(1)请写出图中各对相似三角形(相似比为1除外);
(2)求BP:PQ:QR.
20.(10分)如图,△ABC是一张锐角三角形的硬纸片,AD是边BC上的高,BC
=
40
cm,AD
=
30
cm,从这张硬纸片上剪下一个长HG是宽HE的2倍的矩形EFGH,使它的一边EF在BC上,顶点G,H分别在AC,AB上,AD与HG的交点为M.
(1)求证:
=
;
(2)求这个矩形EFGH的周长.
21.(10分)△ABC中,D是BC上一点,若
=
,则称AD为△ABC的黄金分割线.
(1)求证:若AD为△ABC的黄金分割线,则D是BC的黄金分割点;
(2)若S△ABC
=
20,求△ACD的面积.(结果保留根号)
22.(12分)如图,矩形ABCD的四个顶点A,B,C,D均在正方形网格(网格中正方形的边长为1)的格点(即小正方形的顶点)上.
(1)若AB
=
5,BC
=
2,试在AB边上找点E,使得CE,DE分矩形ABCD所成的三个三角形都相似,请你通过计算找到点E的位置;
(2)若AB
=
5,BC
=
3,能否在AB边上找点E,使得CE,DE分矩形ABCD所成的三个三角形都相似!
请说明你的理由.
23.(12分)如图,在Rt△ABC中,∠ACB
=
90°,AC
=
6
cm,BC
=
8
cm,动点P从点B出发,在BA边上以每秒5
cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4
cm的速度向点B匀速运动,运动时间为t
s(0
<
t
<
2),连结PQ.
(1)若△BPQ与△ABC相似,求t的值;
(2)连结AQ,CP,若AQ⊥CP,求t的值.
同课章节目录
