2020年秋浙教版七年级上册第六章 图形的初步认识 期末复习巩固练习卷(word版含图片答案)
文档属性
| 名称 | 2020年秋浙教版七年级上册第六章 图形的初步认识 期末复习巩固练习卷(word版含图片答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 773.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-29 00:00:00 | ||
图片预览



文档简介
2020学年浙教版八年级第一学期第六章《图形的初步认识》期末复习巩固练习卷
例1:如图所示、B.C两点把线段MN分成三部分,其比为MB:BC:CN
=
2:3:4,点P是MN
的中点,
PC
=
2
cm,求MN的长.
例2:[新知理解]
如图1所示,点C在线段AB上,图中共有三条线段AB,AC和BC,若其中有一条线段的长度是另外一条线段长度的2倍,则称点C是线段AB的“巧点”.
(1)线段的中点
_________
这条线段的“巧点”(填“是”或“不是”).
(2)若AB
=
12
cm,点C是线段AB的“巧点”,则AC
=
_________
cm.
[解决问题]
(3)如图2所示,已知AB
=
12
cm.动点P从点A出发,以2
cm/s的速度沿AB向点B匀速移动,点Q从点B出发,以1
cm/s的速度沿BA向点A匀速移动,点P,Q同时出发,当其中一点到达终点时,运动停止.设移动的时间为t(s).当t为何值时,A,P,Q三点中其中一点恰好是以另外两点为端点的线段的“巧点”?请说明理由.
例3:【问题提出】已知∠AOB
=
70°,∠AOD
=
∠AOC,∠BOD
=
3∠BOC(∠BOC
<
45°),求∠BOC的度数.
【问题思考】聪明的小明用分类讨论的方法解决.
(1)当射线OC在∠AOB的内部时,若射线OD在∠AOC内部,如图1所示,可求∠BOC的度数,解答过程如下:
当射线OC在∠AOB的内部时,若射线OD在∠AOB外部,如图2所示,请你求出∠BOC的度数.
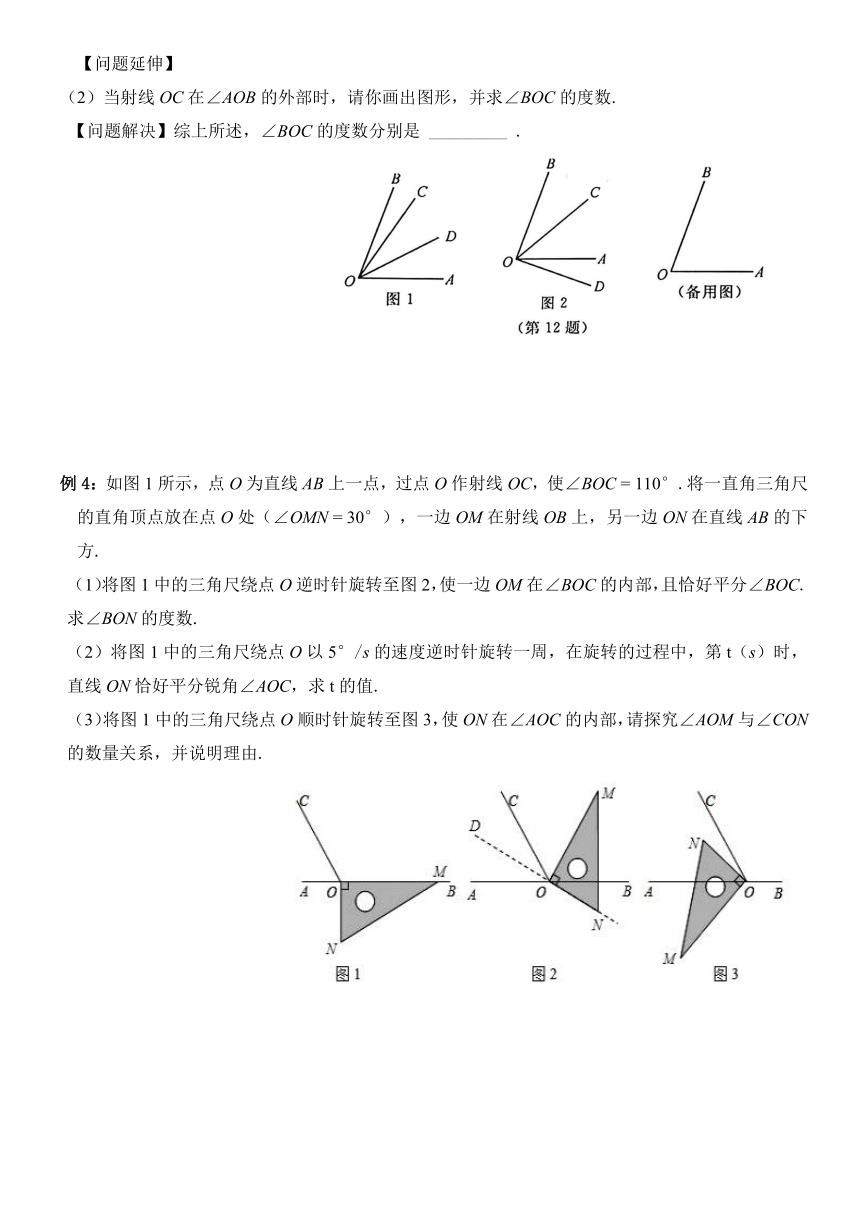
【问题延伸】
(2)当射线OC在∠AOB的外部时,请你画出图形,并求∠BOC的度数.
【问题解决】综上所述,∠BOC的度数分别是
_________
.
例4:如图1所示,点O为直线AB上一点,过点O作射线OC,使∠BOC
=
110°.将一直角三角尺的直角顶点放在点O处(∠OMN
=
30°),一边OM在射线OB上,另一边ON在直线AB的下方.
(1)将图1中的三角尺绕点O逆时针旋转至图2,使一边OM在∠BOC的内部,且恰好平分∠BOC.求∠BON的度数.
(2)将图1中的三角尺绕点O以5°/s的速度逆时针旋转一周,在旋转的过程中,第t(s)时,直线ON恰好平分锐角∠AOC,求t的值.
(3)将图1中的三角尺绕点O顺时针旋转至图3,使ON在∠AOC的内部,请探究∠AOM与∠CON的数量关系,并说明理由.
巩固练习
一、选择题(每小题3分,共30分)
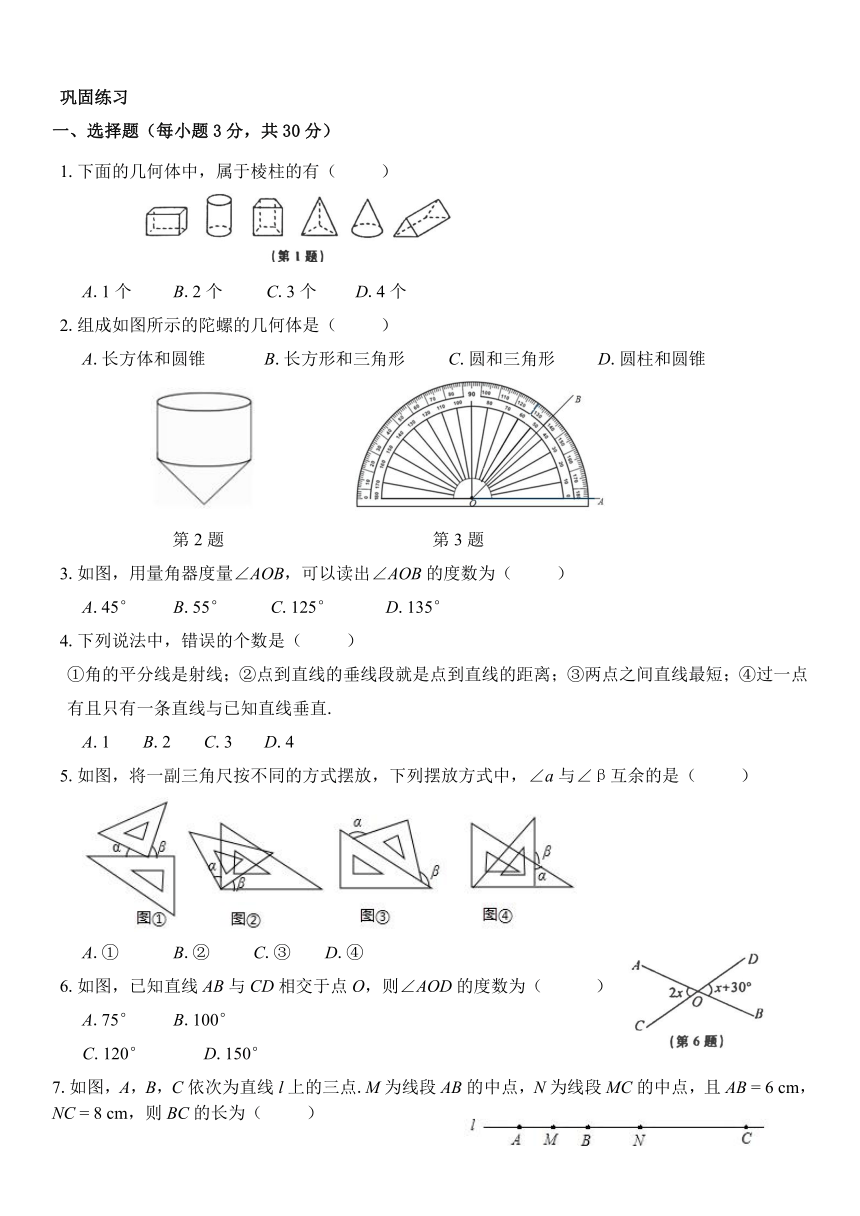
1.下面的几何体中,属于棱柱的有(
)
A.1个
B.2个
C.3个
D.4个
2.组成如图所示的陀螺的几何体是(
)
A.长方体和圆锥
B.长方形和三角形
C.圆和三角形
D.圆柱和圆锥
第2题
第3题
3.如图,用量角器度量∠AOB,可以读出∠AOB的度数为(
)
A.45°
B.55°
C.125°
D.135°
4.下列说法中,错误的个数是(
)
①角的平分线是射线;②点到直线的垂线段就是点到直线的距离;③两点之间直线最短;④过一点有且只有一条直线与已知直线垂直.
A.1
B.2
C.3
D.4
5.如图,将一副三角尺按不同的方式摆放,下列摆放方式中,∠a与∠β互余的是(
)
A.①
B.②
C.③
D.④
6.如图,已知直线AB与CD相交于点O,则∠AOD的度数为( )
A.75°
B.100°
C.120°
D.150°
7.如图,A,B,C依次为直线l上的三点.M为线段AB的中点,N为线段MC的中点,且AB
=
6
cm,NC
=
8
cm,则BC的长为(
)
A.10
cm
B.13
cm
C.14
cm
D.16
cm
8.如图,OB是∠AOC的平分线.∠COD
=
∠BOD,∠COD
=
17°,则∠AOD的度数是(
)
A.68°
B.70°
C.83°
D.85°
9.如图,A,B,C三个车站在东西笔直的一条公路上.现要建一个加油站,使其到三个车站的距离和最小,则加油站应建在(
)
A.A,B之间
B.B,C之间
C.A处
D.B处
10.如图,已知C是线段AB延长线上的一点,M,N分别是线段AB,AC的中点,若MN
=
4
cm,且AB
=
AC,则线段AC的长为( )
A.24
cm
B.32
cm
C.40
cm
D.48
cm
二、填空题(每小题4分,共24分)
11.用度、分、秒表示:32.26°
=
_________
.
12.如图,C为线段AB的中点,点D在线段CB上.若AD
=
9,BD
=
6,则CD的长为
_________
.
13.下午2:20时,钟面上的时针与分针的夹角的度数为
_________
.
14.如图,已知∠AOC
=
∠BOD
=
75°,∠BOC
=
30°,则∠AOD的度数为
15.如图,直线AB,CD相交于点O,OE平分∠AOD,OF⊥OC,∠1与∠3的度数之比为3:4,则∠EOC
=
_________
,∠2
=
_________
.
16.在数学拓展课上,小林对如图所示的长方形纸片ABCD进行如下操作:把△ABF翻折,点B落在CD边上的点E处,折痕为AF,点F在BC边上.把△ADH翻折,点D落在AE边上的点G处,折痕为AH,点H在CD边上.若AD
=
6,AB
=
20-a(0
<
a
<
14),则∠HAF
=
_________
,GE
=
_________
(用含a的代数式表示).
三、解答题(共66分)
17.(6分)如图,根据下列要求画图:(1)画直线BC,线段AB和射线CA.
(2)过点A作AD⊥BC,垂足为D.
18.(6分)如图,已知AD
=
BD,E是BC的中点,BE
=
AC
=
2,求线段DE的长.
19.(6分)如图,直线AB与CD相交于点O,∠BOE
=
∠DOF
=
90°.
(1)写出图中与∠COE互补的所有的角(不用说明理由).
(2)∠COE与∠AOF相等吗?请说明理由.
20.(8分)已知一个角的余角的补角是这个角的补角的,求这个角的余角的度数.
21.(8分)如图,直线AB与CD相交于点O,OP是∠BOC的平分线,OE⊥AB,OF⊥CD.
(1)除直角外,写出图中三对相等的角.
(2)已知∠EOC
=
50°,求∠POF的度数.
22.(10分)如图,已知点O在线段AB上,C,D分别是AO,BO的中点.
(1)AO
=
_________
CO,BO
=
_________
DO.
(2)若CO
=
3
cm,DO
=
2
cm,求线段AB的长.
(3)若线段AB
=
10
cm,小明很轻松地求得CD
=
5
cm.他在反思过程中突发奇想:若点O在线段AB的延长线上,则原有的结论“CD
=
5”是否仍然成立呢?请帮小明画出图形分析,并说明理由.
23.(10分)(1)观察思考:
如图,线段AB上有C,D两点,请写出图中的所有线段.
(2)模型构建:
如果线段上有m个点(包括线段的两个端点),则该线段上共有多少条线段?
(3)拓展应用:
某班45名同学在毕业后的一次聚会中,如果每两人握1次手问好,那么共握多少次手?
24.(12分)如图①,射线OC在∠AOB的内部,图中共有3个角,分别是∠AOB.∠AOC和∠BOC,若其中有一个角的度数为另一个角度数的3倍,则称射线OC是∠AOB的“奇分线”.如图②,已知∠MPN
=
42°.
(1)过点P作射线PQ,若射线PQ是∠MPN的“奇分线”,求∠MPQ.
(2)若射线PE绕点P从PN位置开始,以每秒8°的速度按顺时针方向旋转,当∠EPM首次等于180°时停止旋转.设旋转的时间为t(s),当t为何值时,射线PN是∠EPM的“奇分线”?
例1:如图所示、B.C两点把线段MN分成三部分,其比为MB:BC:CN
=
2:3:4,点P是MN
的中点,
PC
=
2
cm,求MN的长.
例2:[新知理解]
如图1所示,点C在线段AB上,图中共有三条线段AB,AC和BC,若其中有一条线段的长度是另外一条线段长度的2倍,则称点C是线段AB的“巧点”.
(1)线段的中点
_________
这条线段的“巧点”(填“是”或“不是”).
(2)若AB
=
12
cm,点C是线段AB的“巧点”,则AC
=
_________
cm.
[解决问题]
(3)如图2所示,已知AB
=
12
cm.动点P从点A出发,以2
cm/s的速度沿AB向点B匀速移动,点Q从点B出发,以1
cm/s的速度沿BA向点A匀速移动,点P,Q同时出发,当其中一点到达终点时,运动停止.设移动的时间为t(s).当t为何值时,A,P,Q三点中其中一点恰好是以另外两点为端点的线段的“巧点”?请说明理由.
例3:【问题提出】已知∠AOB
=
70°,∠AOD
=
∠AOC,∠BOD
=
3∠BOC(∠BOC
<
45°),求∠BOC的度数.
【问题思考】聪明的小明用分类讨论的方法解决.
(1)当射线OC在∠AOB的内部时,若射线OD在∠AOC内部,如图1所示,可求∠BOC的度数,解答过程如下:
当射线OC在∠AOB的内部时,若射线OD在∠AOB外部,如图2所示,请你求出∠BOC的度数.
【问题延伸】
(2)当射线OC在∠AOB的外部时,请你画出图形,并求∠BOC的度数.
【问题解决】综上所述,∠BOC的度数分别是
_________
.
例4:如图1所示,点O为直线AB上一点,过点O作射线OC,使∠BOC
=
110°.将一直角三角尺的直角顶点放在点O处(∠OMN
=
30°),一边OM在射线OB上,另一边ON在直线AB的下方.
(1)将图1中的三角尺绕点O逆时针旋转至图2,使一边OM在∠BOC的内部,且恰好平分∠BOC.求∠BON的度数.
(2)将图1中的三角尺绕点O以5°/s的速度逆时针旋转一周,在旋转的过程中,第t(s)时,直线ON恰好平分锐角∠AOC,求t的值.
(3)将图1中的三角尺绕点O顺时针旋转至图3,使ON在∠AOC的内部,请探究∠AOM与∠CON的数量关系,并说明理由.
巩固练习
一、选择题(每小题3分,共30分)
1.下面的几何体中,属于棱柱的有(
)
A.1个
B.2个
C.3个
D.4个
2.组成如图所示的陀螺的几何体是(
)
A.长方体和圆锥
B.长方形和三角形
C.圆和三角形
D.圆柱和圆锥
第2题
第3题
3.如图,用量角器度量∠AOB,可以读出∠AOB的度数为(
)
A.45°
B.55°
C.125°
D.135°
4.下列说法中,错误的个数是(
)
①角的平分线是射线;②点到直线的垂线段就是点到直线的距离;③两点之间直线最短;④过一点有且只有一条直线与已知直线垂直.
A.1
B.2
C.3
D.4
5.如图,将一副三角尺按不同的方式摆放,下列摆放方式中,∠a与∠β互余的是(
)
A.①
B.②
C.③
D.④
6.如图,已知直线AB与CD相交于点O,则∠AOD的度数为( )
A.75°
B.100°
C.120°
D.150°
7.如图,A,B,C依次为直线l上的三点.M为线段AB的中点,N为线段MC的中点,且AB
=
6
cm,NC
=
8
cm,则BC的长为(
)
A.10
cm
B.13
cm
C.14
cm
D.16
cm
8.如图,OB是∠AOC的平分线.∠COD
=
∠BOD,∠COD
=
17°,则∠AOD的度数是(
)
A.68°
B.70°
C.83°
D.85°
9.如图,A,B,C三个车站在东西笔直的一条公路上.现要建一个加油站,使其到三个车站的距离和最小,则加油站应建在(
)
A.A,B之间
B.B,C之间
C.A处
D.B处
10.如图,已知C是线段AB延长线上的一点,M,N分别是线段AB,AC的中点,若MN
=
4
cm,且AB
=
AC,则线段AC的长为( )
A.24
cm
B.32
cm
C.40
cm
D.48
cm
二、填空题(每小题4分,共24分)
11.用度、分、秒表示:32.26°
=
_________
.
12.如图,C为线段AB的中点,点D在线段CB上.若AD
=
9,BD
=
6,则CD的长为
_________
.
13.下午2:20时,钟面上的时针与分针的夹角的度数为
_________
.
14.如图,已知∠AOC
=
∠BOD
=
75°,∠BOC
=
30°,则∠AOD的度数为
15.如图,直线AB,CD相交于点O,OE平分∠AOD,OF⊥OC,∠1与∠3的度数之比为3:4,则∠EOC
=
_________
,∠2
=
_________
.
16.在数学拓展课上,小林对如图所示的长方形纸片ABCD进行如下操作:把△ABF翻折,点B落在CD边上的点E处,折痕为AF,点F在BC边上.把△ADH翻折,点D落在AE边上的点G处,折痕为AH,点H在CD边上.若AD
=
6,AB
=
20-a(0
<
a
<
14),则∠HAF
=
_________
,GE
=
_________
(用含a的代数式表示).
三、解答题(共66分)
17.(6分)如图,根据下列要求画图:(1)画直线BC,线段AB和射线CA.
(2)过点A作AD⊥BC,垂足为D.
18.(6分)如图,已知AD
=
BD,E是BC的中点,BE
=
AC
=
2,求线段DE的长.
19.(6分)如图,直线AB与CD相交于点O,∠BOE
=
∠DOF
=
90°.
(1)写出图中与∠COE互补的所有的角(不用说明理由).
(2)∠COE与∠AOF相等吗?请说明理由.
20.(8分)已知一个角的余角的补角是这个角的补角的,求这个角的余角的度数.
21.(8分)如图,直线AB与CD相交于点O,OP是∠BOC的平分线,OE⊥AB,OF⊥CD.
(1)除直角外,写出图中三对相等的角.
(2)已知∠EOC
=
50°,求∠POF的度数.
22.(10分)如图,已知点O在线段AB上,C,D分别是AO,BO的中点.
(1)AO
=
_________
CO,BO
=
_________
DO.
(2)若CO
=
3
cm,DO
=
2
cm,求线段AB的长.
(3)若线段AB
=
10
cm,小明很轻松地求得CD
=
5
cm.他在反思过程中突发奇想:若点O在线段AB的延长线上,则原有的结论“CD
=
5”是否仍然成立呢?请帮小明画出图形分析,并说明理由.
23.(10分)(1)观察思考:
如图,线段AB上有C,D两点,请写出图中的所有线段.
(2)模型构建:
如果线段上有m个点(包括线段的两个端点),则该线段上共有多少条线段?
(3)拓展应用:
某班45名同学在毕业后的一次聚会中,如果每两人握1次手问好,那么共握多少次手?
24.(12分)如图①,射线OC在∠AOB的内部,图中共有3个角,分别是∠AOB.∠AOC和∠BOC,若其中有一个角的度数为另一个角度数的3倍,则称射线OC是∠AOB的“奇分线”.如图②,已知∠MPN
=
42°.
(1)过点P作射线PQ,若射线PQ是∠MPN的“奇分线”,求∠MPQ.
(2)若射线PE绕点P从PN位置开始,以每秒8°的速度按顺时针方向旋转,当∠EPM首次等于180°时停止旋转.设旋转的时间为t(s),当t为何值时,射线PN是∠EPM的“奇分线”?
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
