6.3正方形

(共11张PPT)
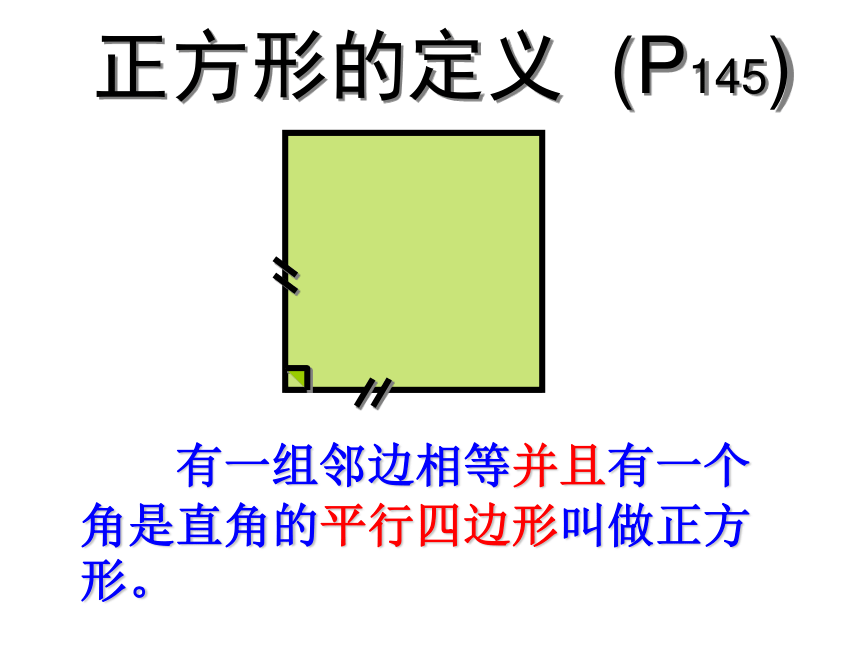
正方形的定义 (P145)
有一组邻边相等并且有一个角是直角的平行四边形叫做正方形。
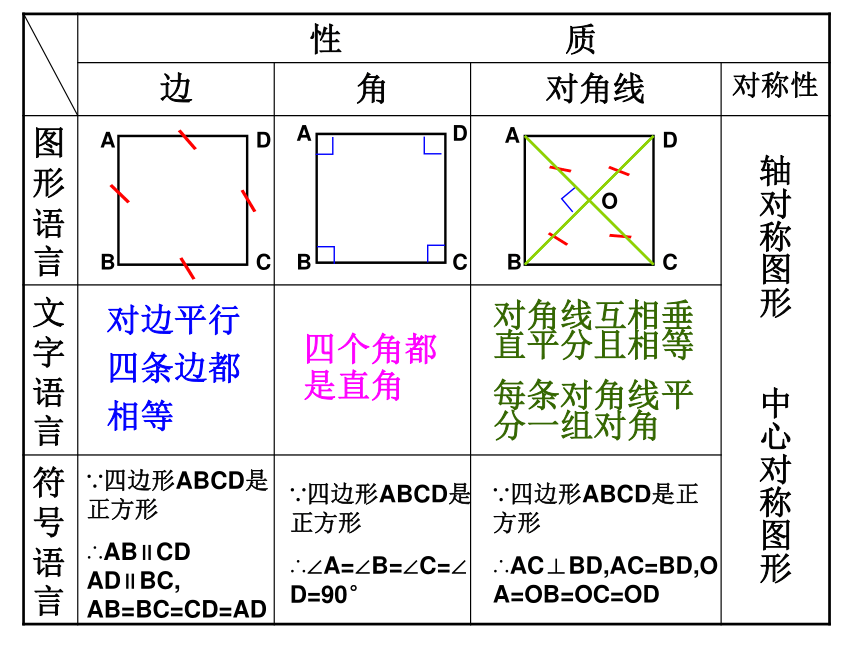
性 质
边 角 对角线 对称性
图形语言
文字语言
符号语言
A
C
D
\
B
A
C
D
B
A
C
D
B
\
\
\
∟
∟
∟
∟
O
\
\
\
\
∟
对边平行
四条边都
相等
四个角都
是直角
对角线互相垂直平分且相等
每条对角线平分一组对角
∵四边形ABCD是正方形
∴AB∥CD AD∥BC, AB=BC=CD=AD
∵四边形ABCD是正方形
∴∠A=∠B=∠C=∠D=90°
∵四边形ABCD是正方形
∴AC⊥BD,AC=BD,OA=OB=OC=OD
轴对称图形 中心对称图形
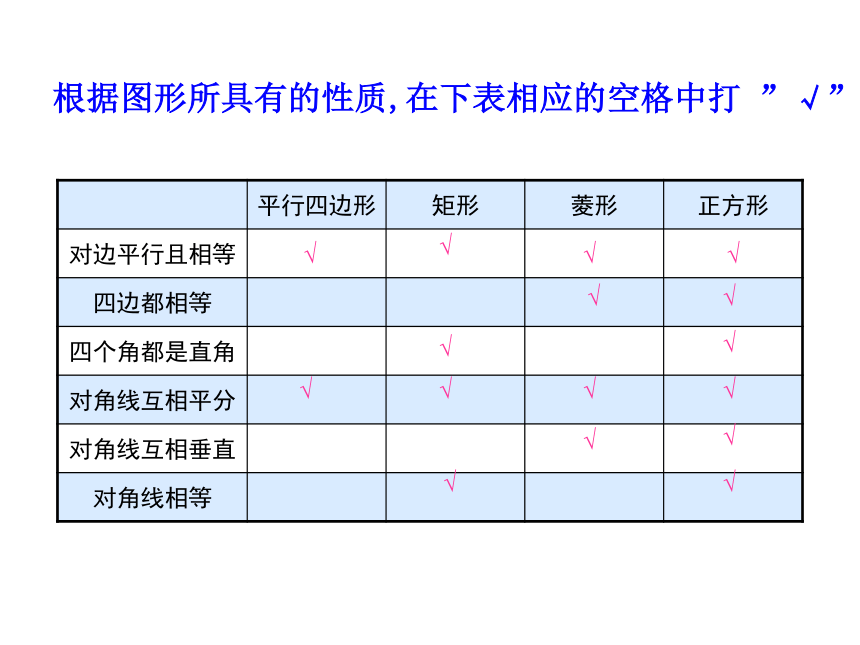
根据图形所具有的性质,在下表相应的空格中打 ”√”
平行四边形 矩形 菱形 正方形
对边平行且相等
四边都相等
四个角都是直角
对角线互相平分
对角线互相垂直
对角线相等
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
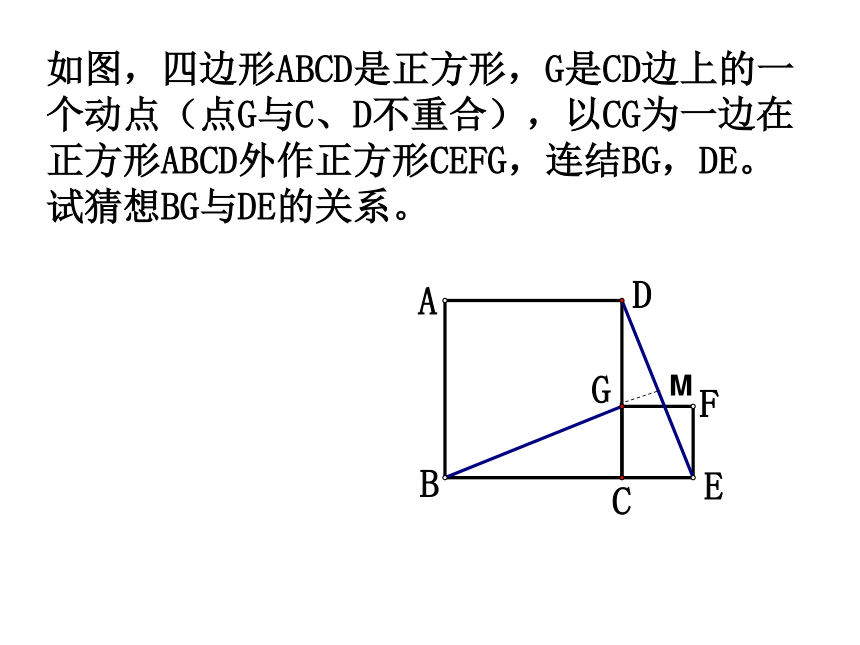
如图，四边形ABCD是正方形，G是CD边上的一个动点（点G与C、D不重合），以CG为一边在正方形ABCD外作正方形CEFG，连结BG，DE。试猜想BG与DE的关系。
M
具备什么条件的四边形是正方形？
2、先说明它是矩形，再说明这个矩形有一组邻边相等。
3、先说明它是菱形，再说明这个菱形有一个角是直角。
1、先说明它是平行四边形，再说明有一组邻边相等，有一个角是直角。
矩形
菱形
(2)
(1)
平行四边形
正方形
A
B
C
D
O
(1) AB＝AD (2) AC=BD
(3)∠BAD=90° (4)AC⊥BD
D
A
B
C
O
(3)
(4)
矩形
菱形
(2)
(1)
平行四边形
正方形
A
B
C
D
O
(1) AB＝AD (2) AC=BD
(3)∠BAD=90° (4)AC⊥BD
D
A
B
C
O
(3)
(4)
已知：如图，在Rt△ABC中，∠ACB=90°，CD是∠ACB的平分线，过点D作DE‖AC，DF‖BC分别交BC、AC于点E、F。
求证：四边形CFDE是正方形。
已知正方形ABCD中，E是AD上一点，过BE上一点O作BE的垂线，交AB于点G，交CD于点H，求证：BE=GH。
M
正方形的特征
1、正方形是特殊的平行四边形，具备平行四边形的所有特征。
2、正方形是特殊的矩形和菱形，具备它们的所有特征。
3、正方形的四条边都相等。
4、正方形的两条对角线互相垂直平分且相等，并且分别平分每一组对角。
5、正方形即是轴对称图形、又是中心对称图形。