浙教版九年级数学下册 第2章 直线与圆的位置关系 单元检测试题(word版,有答案)
文档属性
| 名称 | 浙教版九年级数学下册 第2章 直线与圆的位置关系 单元检测试题(word版,有答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 254.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-02 00:00:00 | ||
图片预览


文档简介
第2章
直线与圆的位置关系
单元检测试题
(满分100分;时间:90分钟)
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
)
?1.
已知的半径为,如果一条直线和圆心的距离为,那么这条直线和这个圆的位置关系为(
)
A.相离
B.相交
C.相切
D.相切或相离
?
2.
已知,,为内心,交于,,,则
A.
B.
C.
D.
?
3.
如图,是的内切圆,,若,,则的半径(
)
A.
B.
C.
D.
?
4.
已知的半径是,点到直线的距离是,则直线与
A.相切
B.相交
C.相离
D.以上都不是
?
5.
半径为的和直线上一点,且,则直线与的位置关系是?
?
?
?
A.相切
B.相交
C.相离
D.相切或相交
?
6.
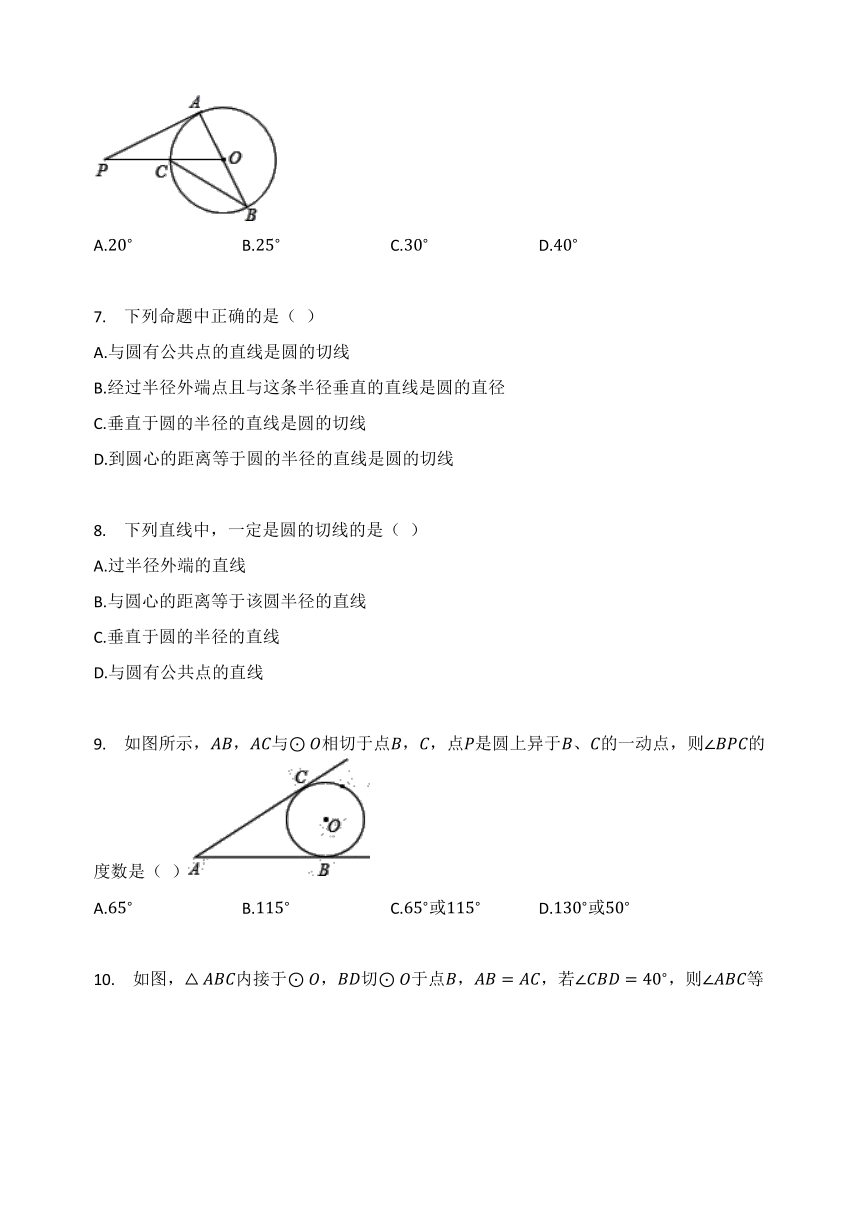
是的直径,切于点,交于点;连接,若=,则等于(
)
A.
B.
C.
D.
?
7.
下列命题中正确的是(
)
A.与圆有公共点的直线是圆的切线
B.经过半径外端点且与这条半径垂直的直线是圆的直径
C.垂直于圆的半径的直线是圆的切线
D.到圆心的距离等于圆的半径的直线是圆的切线
?
8.
下列直线中,一定是圆的切线的是(
)
A.过半径外端的直线
B.与圆心的距离等于该圆半径的直线
C.垂直于圆的半径的直线
D.与圆有公共点的直线
?
9.
如图所示,,与相切于点,,点是圆上异于、的一动点,则的度数是(
)
A.
B.
C.或
D.或
?
10.
如图,内接于,切于点,,若,则等于(
)
A.
B.
C.
D.
二、
填空题
(本题共计
10
小题
,每题
3
分
,共计30分
)
?
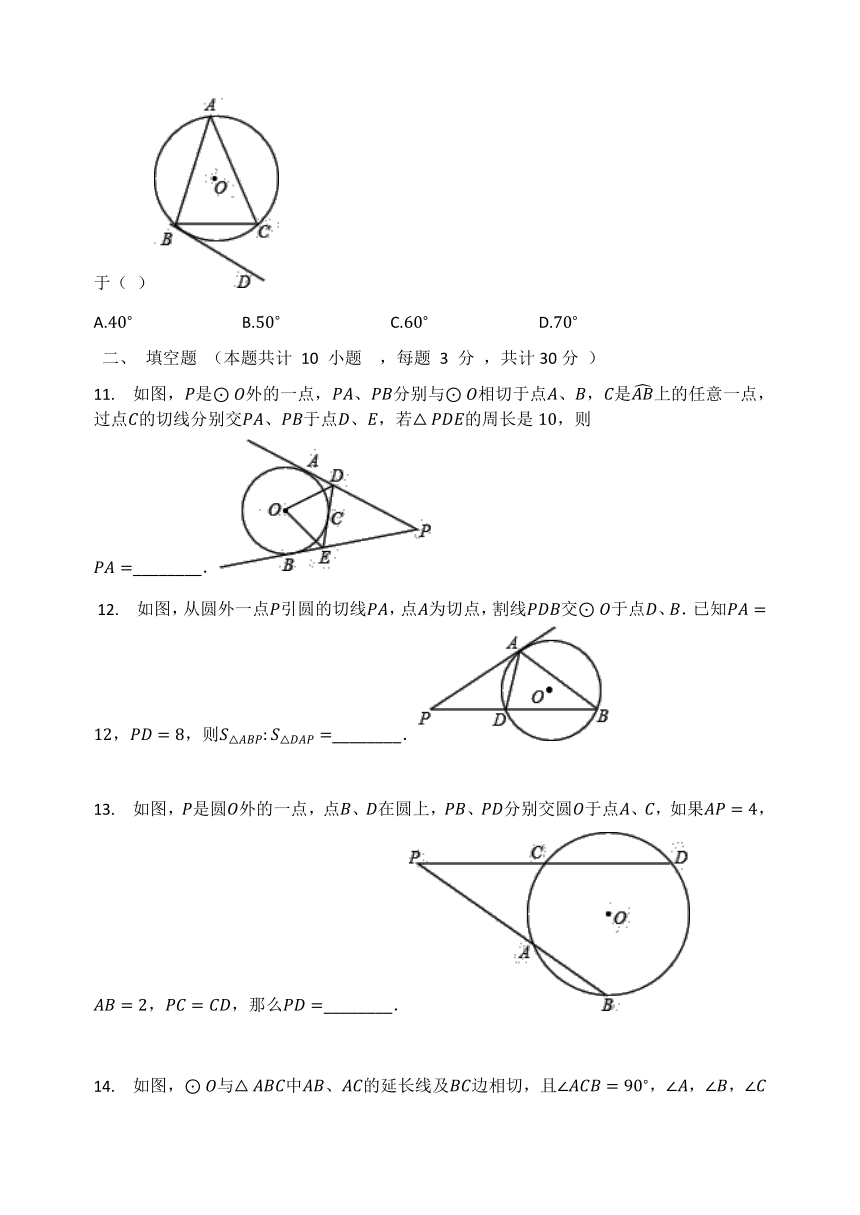
11.
如图,是外的一点,、分别与相切于点、,是上的任意一点,过点的切线分别交、于点、,若的周长是,则________.
?12.
如图,从圆外一点引圆的切线,点为切点,割线交于点、.已知,,则________.
?
13.
如图,是圆外的一点,点、在圆上,、分别交圆于点、,如果,,,那么________.
?
14.
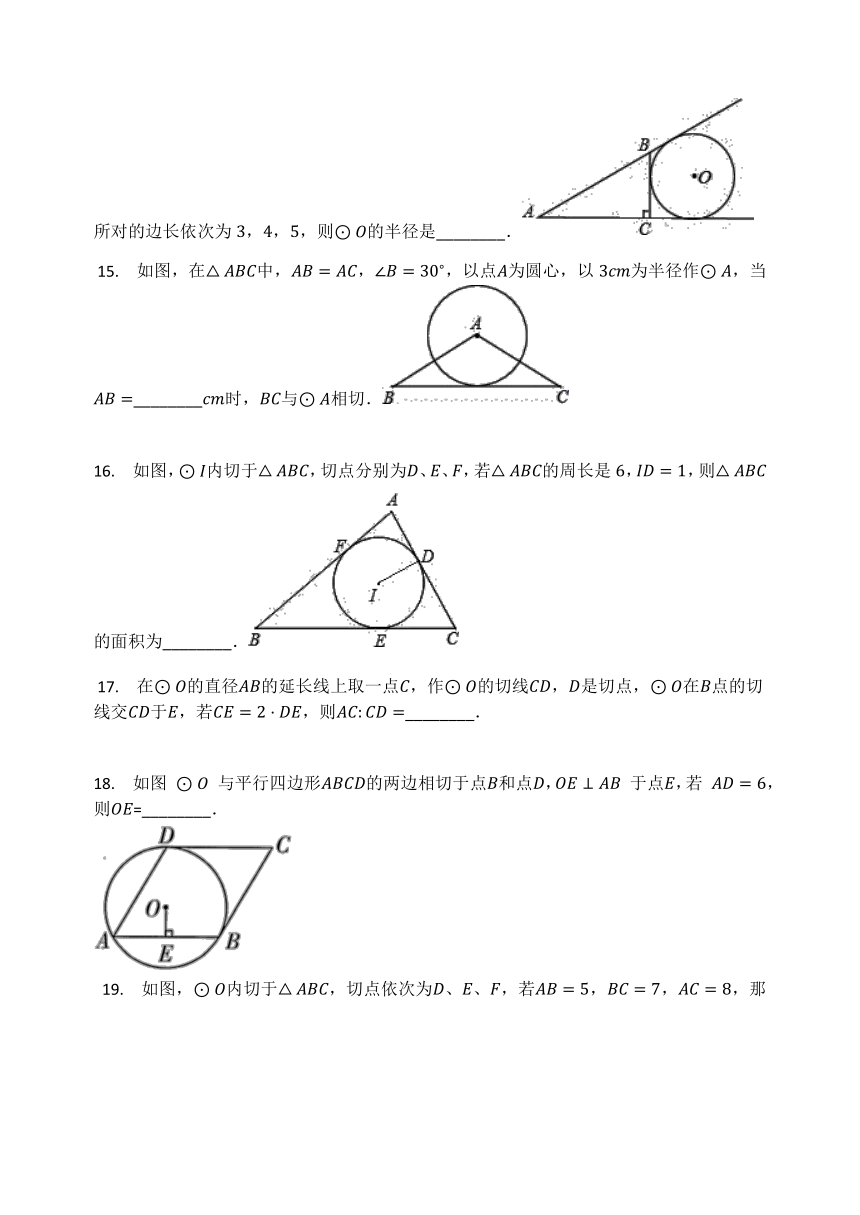
如图,与中、的延长线及边相切,且,,,所对的边长依次为,,,则的半径是________.
?15.
如图,在中,,,以点为圆心,以为半径作,当________时,与相切.
?
16.
如图,内切于,切点分别为、、,若的周长是,,则的面积为________.
?17.
在的直径的延长线上取一点,作的切线,是切点,在点的切线交于,若,则________.
?
18.
如图
与平行四边形的两边相切于点和点,
于点,若
,则=________.
19.
如图,内切于,切点依次为、、,若,,,那么________,________,________.
?
20.
如图,小明同学测量一个光盘的直径,他只有一把直尺和一块三角板,他将直尺、光盘和三角板如图放置于桌面上,并量出,则此光盘的半径是________.
三、
解答题
(本题共计
6
小题
,共计60分
)
?
21.
在中,,的平分线交于点,点是上一点,过、两点,且分别交、于点、.
求证:是的切线.
?
22.
如图,为的直径,平分,交于点,过点作直线,交的延长线于点,交的延长线于点.
求证:是的切线.
若,,求的半径及的长.
?
23.
如图,直线与相切于点,是弦所对的圆周角,试判断与的大小关系.
?
24.
如图,在中,,的平分线交于点,以点为圆心,长为半径作求证:与相切.
?
25.
如图,分别切、、于、、三点,若的周长为,求的长.
?
26.
如图,是的切线,切点为,是的割线,交于、两点,半径,垂足为,交于点,.
(1)求证:;
(2)若,求切线的长.
参考答案
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
)
1.
【答案】
B
【解答】
解:∵
直线的距离,
∴
直线和圆相交.
故选.
2.
【答案】
B
【解答】
解:∵
为内心,
∴
平分,
∴
,
设,,
∴
,
∴
,解得,
∴
,,
∴
.
故选.
3.
【答案】
A
【解答】
解:如图:连接,,
在,,,,
根据勾股定理,
四边形中,,,
∴
四边形是正方形,
由切线长定理,得:,,,
∴
,
即.
故选:.
4.
【答案】
B
【解答】
解:∵
的半径为,圆心到直线的距离为,
∵
,即:,
∴
直线与的位置关系是相交.
故选.
5.
【答案】
D
【解答】
解:设圆心到直线的距离为,则,当时,,直线与圆相切;
当时,,直线与圆相交,所以直线与圆相切或相交.
故选.
6.
【答案】
B
【解答】
∵
切于点,
∴
=,
∵
=,
∴
==,
∵
=,
∴
==,
7.
【答案】
D
【解答】
解:、割线与圆相交也有公共点,但不是圆的切线,故不正确;
、符合切线的概念,而不是圆的直径,故不正确;
、应该为经过半径外端点且与这条半径垂直的直线是圆的切线,故不正确;
、符合圆的切线概念,故正确;
故选.
8.
【答案】
B
【解答】
解:切线的判定定理有:①经过半径的外端且垂直于这条半径的直线是圆的切线,②与圆心的距离等于该圆的半径的直线是圆的切线,
、如图不是的切线,故本选项错误;
、与圆心的距离等于该圆的半径的直线是圆的切线,故本选项正确;
、如图,半径,但不是的切线,故本选项错误;
、如上图,有公共点,但不是的切线,故本选项错误;
故选.
9.
【答案】
C
【解答】
解:分别连接、;、;、;、;、;、各点
当为锐角,也就是时:
∵
,与相切于点,两点
∴
,,
∵
,
∴
在中,,
∵
在中,为圆周角,
∴
,
如果当为钝角,也就是时
∵
四边形为的内接四边形,
∵
,
∴
,
故的度数是或.
故选:.
10.
【答案】
D
【解答】
解:∵
切于点,
∴
,
∵
,
∴
,
∴
.
故选.
二、
填空题
(本题共计
10
小题
,每题
3
分
,共计30分
)
11.
【答案】
【解答】
解:∵
,都是圆的切线,
∴
,
同理,,
∴
的周长,
∴
;
故答案为.
12.
【答案】
【解答】
解:由切割线定理可得,
∵
,
∴
.
由弦切角和公共角易知.
∴
.
13.
【答案】
【解答】
解:如图,∵
,,,
∴
,.
又∵
,
∴
,
则.
故答案是:.
14.
【答案】
【解答】
解:连接、,
∵
与中、的延长线及边相切,
∴
,,,
,,
∵
,
∴
四边形是正方形,
设,则,
∵
,
∴
,
∵
,,
∴
,
,
∴
,
,
则的半径是.
故答案为:.
15.
【答案】
【解答】
解:如图,过点作于点.
∵
,,
∴
,即.
又∵
与相切,
∴
就是圆的半径,
∴
,
则.
故答案是:.
16.
【答案】
【解答】
解:分别连接,,,,,由图可知
.
17.
【答案】
【解答】
解:设,则,在中,,
由切割线定理得,
∴
,
故.
18.
【答案】
【解答】
此题暂无解答
19.
【答案】
,,
【解答】
解:∵
内切于,切点依次为、、,,,,
∴
,,,设,则,
∴
,,
∴
,
解得:,
∴
,,
故答案为:,,.
20.
【答案】
【解答】
解:连接,
∵
,
∴
,
∵
和与相切,
∴
,
∴
∵
,
∴
,
∴
由勾股定理得,
∴
光盘的半径是.
故答案为:.
三、
解答题
(本题共计
6
小题
,每题
10
分
,共计60分
)
21.
【答案】
解:连接,
∵
的平分线交于点,
∴
,
∵
,
∴
,
∴
,
∵
,
∴
,
∴
是的切线.
【解答】
解:连接,
∵
的平分线交于点,
∴
,
∵
,
∴
,
∴
,
∵
,
∴
,
∴
是的切线.
22.
【答案】
证明:连接;
∵
是的平分线,
∴
.
∵
,
∴
.
∴
.
∴
,
∵
,
∴
.
∴
.
∴
是的切线.
解:连接,
∵
,,
根据切割线定理:,
∴
,
∴
,
∵
为的直径,
∴
的半径为,
∵
是的切线,
∴
,
∵
,
∴
,
∴
,
∴
,
∵
为的直径,
∴
,
∴
,即,
∴
.
【解答】
证明:连接;
∵
是的平分线,
∴
.
∵
,
∴
.
∴
.
∴
,
∵
,
∴
.
∴
.
∴
是的切线.
解:连接,
∵
,,
根据切割线定理:,
∴
,
∴
,
∵
为的直径,
∴
的半径为,
∵
是的切线,
∴
,
∵
,
∴
,
∴
,
∴
,
∵
为的直径,
∴
,
∴
,即,
∴
.
23.
【答案】
解:如图,作直径,连接,
;
证明:∵
是的直径,
∴
;
又∵
是的切线,
∴
,
∴
;
∴
.
【解答】
解:如图,作直径,连接,
;
证明:∵
是的直径,
∴
;
又∵
是的切线,
∴
,
∴
;
∴
.
24.
【答案】
证明:作于点,
∵
平分,,
∴
,
∴
与☉相切.
【解答】
证明:作于点,
∵
平分,,
∴
,
∴
与☉相切.
25.
【答案】
解:∵
、切于、,
∴
;
同理,可得:,;
∴
的周长.
则.
【解答】
解:∵
、切于、,
∴
;
同理,可得:,;
∴
的周长.
则.
26.
【答案】
(1)证明:∵
是圆的切线,
∴
…①
∵
,
∴
…②
∵
,
∴
,而.
∴
…③
根据①②③可得:,
∴
.
(2)解:∵
是圆的切线,
∴
.
∵
,,
∴
.
∴
.
【解答】
(1)证明:∵
是圆的切线,
∴
…①
∵
,
∴
…②
∵
,
∴
,而.
∴
…③
根据①②③可得:,
∴
.
(2)解:∵
是圆的切线,
∴
.
∵
,,
∴
.
∴
.
直线与圆的位置关系
单元检测试题
(满分100分;时间:90分钟)
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
)
?1.
已知的半径为,如果一条直线和圆心的距离为,那么这条直线和这个圆的位置关系为(
)
A.相离
B.相交
C.相切
D.相切或相离
?
2.
已知,,为内心,交于,,,则
A.
B.
C.
D.
?
3.
如图,是的内切圆,,若,,则的半径(
)
A.
B.
C.
D.
?
4.
已知的半径是,点到直线的距离是,则直线与
A.相切
B.相交
C.相离
D.以上都不是
?
5.
半径为的和直线上一点,且,则直线与的位置关系是?
?
?
?
A.相切
B.相交
C.相离
D.相切或相交
?
6.
是的直径,切于点,交于点;连接,若=,则等于(
)
A.
B.
C.
D.
?
7.
下列命题中正确的是(
)
A.与圆有公共点的直线是圆的切线
B.经过半径外端点且与这条半径垂直的直线是圆的直径
C.垂直于圆的半径的直线是圆的切线
D.到圆心的距离等于圆的半径的直线是圆的切线
?
8.
下列直线中,一定是圆的切线的是(
)
A.过半径外端的直线
B.与圆心的距离等于该圆半径的直线
C.垂直于圆的半径的直线
D.与圆有公共点的直线
?
9.
如图所示,,与相切于点,,点是圆上异于、的一动点,则的度数是(
)
A.
B.
C.或
D.或
?
10.
如图,内接于,切于点,,若,则等于(
)
A.
B.
C.
D.
二、
填空题
(本题共计
10
小题
,每题
3
分
,共计30分
)
?
11.
如图,是外的一点,、分别与相切于点、,是上的任意一点,过点的切线分别交、于点、,若的周长是,则________.
?12.
如图,从圆外一点引圆的切线,点为切点,割线交于点、.已知,,则________.
?
13.
如图,是圆外的一点,点、在圆上,、分别交圆于点、,如果,,,那么________.
?
14.
如图,与中、的延长线及边相切,且,,,所对的边长依次为,,,则的半径是________.
?15.
如图,在中,,,以点为圆心,以为半径作,当________时,与相切.
?
16.
如图,内切于,切点分别为、、,若的周长是,,则的面积为________.
?17.
在的直径的延长线上取一点,作的切线,是切点,在点的切线交于,若,则________.
?
18.
如图
与平行四边形的两边相切于点和点,
于点,若
,则=________.
19.
如图,内切于,切点依次为、、,若,,,那么________,________,________.
?
20.
如图,小明同学测量一个光盘的直径,他只有一把直尺和一块三角板,他将直尺、光盘和三角板如图放置于桌面上,并量出,则此光盘的半径是________.
三、
解答题
(本题共计
6
小题
,共计60分
)
?
21.
在中,,的平分线交于点,点是上一点,过、两点,且分别交、于点、.
求证:是的切线.
?
22.
如图,为的直径,平分,交于点,过点作直线,交的延长线于点,交的延长线于点.
求证:是的切线.
若,,求的半径及的长.
?
23.
如图,直线与相切于点,是弦所对的圆周角,试判断与的大小关系.
?
24.
如图,在中,,的平分线交于点,以点为圆心,长为半径作求证:与相切.
?
25.
如图,分别切、、于、、三点,若的周长为,求的长.
?
26.
如图,是的切线,切点为,是的割线,交于、两点,半径,垂足为,交于点,.
(1)求证:;
(2)若,求切线的长.
参考答案
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
)
1.
【答案】
B
【解答】
解:∵
直线的距离,
∴
直线和圆相交.
故选.
2.
【答案】
B
【解答】
解:∵
为内心,
∴
平分,
∴
,
设,,
∴
,
∴
,解得,
∴
,,
∴
.
故选.
3.
【答案】
A
【解答】
解:如图:连接,,
在,,,,
根据勾股定理,
四边形中,,,
∴
四边形是正方形,
由切线长定理,得:,,,
∴
,
即.
故选:.
4.
【答案】
B
【解答】
解:∵
的半径为,圆心到直线的距离为,
∵
,即:,
∴
直线与的位置关系是相交.
故选.
5.
【答案】
D
【解答】
解:设圆心到直线的距离为,则,当时,,直线与圆相切;
当时,,直线与圆相交,所以直线与圆相切或相交.
故选.
6.
【答案】
B
【解答】
∵
切于点,
∴
=,
∵
=,
∴
==,
∵
=,
∴
==,
7.
【答案】
D
【解答】
解:、割线与圆相交也有公共点,但不是圆的切线,故不正确;
、符合切线的概念,而不是圆的直径,故不正确;
、应该为经过半径外端点且与这条半径垂直的直线是圆的切线,故不正确;
、符合圆的切线概念,故正确;
故选.
8.
【答案】
B
【解答】
解:切线的判定定理有:①经过半径的外端且垂直于这条半径的直线是圆的切线,②与圆心的距离等于该圆的半径的直线是圆的切线,
、如图不是的切线,故本选项错误;
、与圆心的距离等于该圆的半径的直线是圆的切线,故本选项正确;
、如图,半径,但不是的切线,故本选项错误;
、如上图,有公共点,但不是的切线,故本选项错误;
故选.
9.
【答案】
C
【解答】
解:分别连接、;、;、;、;、;、各点
当为锐角,也就是时:
∵
,与相切于点,两点
∴
,,
∵
,
∴
在中,,
∵
在中,为圆周角,
∴
,
如果当为钝角,也就是时
∵
四边形为的内接四边形,
∵
,
∴
,
故的度数是或.
故选:.
10.
【答案】
D
【解答】
解:∵
切于点,
∴
,
∵
,
∴
,
∴
.
故选.
二、
填空题
(本题共计
10
小题
,每题
3
分
,共计30分
)
11.
【答案】
【解答】
解:∵
,都是圆的切线,
∴
,
同理,,
∴
的周长,
∴
;
故答案为.
12.
【答案】
【解答】
解:由切割线定理可得,
∵
,
∴
.
由弦切角和公共角易知.
∴
.
13.
【答案】
【解答】
解:如图,∵
,,,
∴
,.
又∵
,
∴
,
则.
故答案是:.
14.
【答案】
【解答】
解:连接、,
∵
与中、的延长线及边相切,
∴
,,,
,,
∵
,
∴
四边形是正方形,
设,则,
∵
,
∴
,
∵
,,
∴
,
,
∴
,
,
则的半径是.
故答案为:.
15.
【答案】
【解答】
解:如图,过点作于点.
∵
,,
∴
,即.
又∵
与相切,
∴
就是圆的半径,
∴
,
则.
故答案是:.
16.
【答案】
【解答】
解:分别连接,,,,,由图可知
.
17.
【答案】
【解答】
解:设,则,在中,,
由切割线定理得,
∴
,
故.
18.
【答案】
【解答】
此题暂无解答
19.
【答案】
,,
【解答】
解:∵
内切于,切点依次为、、,,,,
∴
,,,设,则,
∴
,,
∴
,
解得:,
∴
,,
故答案为:,,.
20.
【答案】
【解答】
解:连接,
∵
,
∴
,
∵
和与相切,
∴
,
∴
∵
,
∴
,
∴
由勾股定理得,
∴
光盘的半径是.
故答案为:.
三、
解答题
(本题共计
6
小题
,每题
10
分
,共计60分
)
21.
【答案】
解:连接,
∵
的平分线交于点,
∴
,
∵
,
∴
,
∴
,
∵
,
∴
,
∴
是的切线.
【解答】
解:连接,
∵
的平分线交于点,
∴
,
∵
,
∴
,
∴
,
∵
,
∴
,
∴
是的切线.
22.
【答案】
证明:连接;
∵
是的平分线,
∴
.
∵
,
∴
.
∴
.
∴
,
∵
,
∴
.
∴
.
∴
是的切线.
解:连接,
∵
,,
根据切割线定理:,
∴
,
∴
,
∵
为的直径,
∴
的半径为,
∵
是的切线,
∴
,
∵
,
∴
,
∴
,
∴
,
∵
为的直径,
∴
,
∴
,即,
∴
.
【解答】
证明:连接;
∵
是的平分线,
∴
.
∵
,
∴
.
∴
.
∴
,
∵
,
∴
.
∴
.
∴
是的切线.
解:连接,
∵
,,
根据切割线定理:,
∴
,
∴
,
∵
为的直径,
∴
的半径为,
∵
是的切线,
∴
,
∵
,
∴
,
∴
,
∴
,
∵
为的直径,
∴
,
∴
,即,
∴
.
23.
【答案】
解:如图,作直径,连接,
;
证明:∵
是的直径,
∴
;
又∵
是的切线,
∴
,
∴
;
∴
.
【解答】
解:如图,作直径,连接,
;
证明:∵
是的直径,
∴
;
又∵
是的切线,
∴
,
∴
;
∴
.
24.
【答案】
证明:作于点,
∵
平分,,
∴
,
∴
与☉相切.
【解答】
证明:作于点,
∵
平分,,
∴
,
∴
与☉相切.
25.
【答案】
解:∵
、切于、,
∴
;
同理,可得:,;
∴
的周长.
则.
【解答】
解:∵
、切于、,
∴
;
同理,可得:,;
∴
的周长.
则.
26.
【答案】
(1)证明:∵
是圆的切线,
∴
…①
∵
,
∴
…②
∵
,
∴
,而.
∴
…③
根据①②③可得:,
∴
.
(2)解:∵
是圆的切线,
∴
.
∵
,,
∴
.
∴
.
【解答】
(1)证明:∵
是圆的切线,
∴
…①
∵
,
∴
…②
∵
,
∴
,而.
∴
…③
根据①②③可得:,
∴
.
(2)解:∵
是圆的切线,
∴
.
∵
,,
∴
.
∴
.
