1.4 绝对值 课件

(共17张PPT)
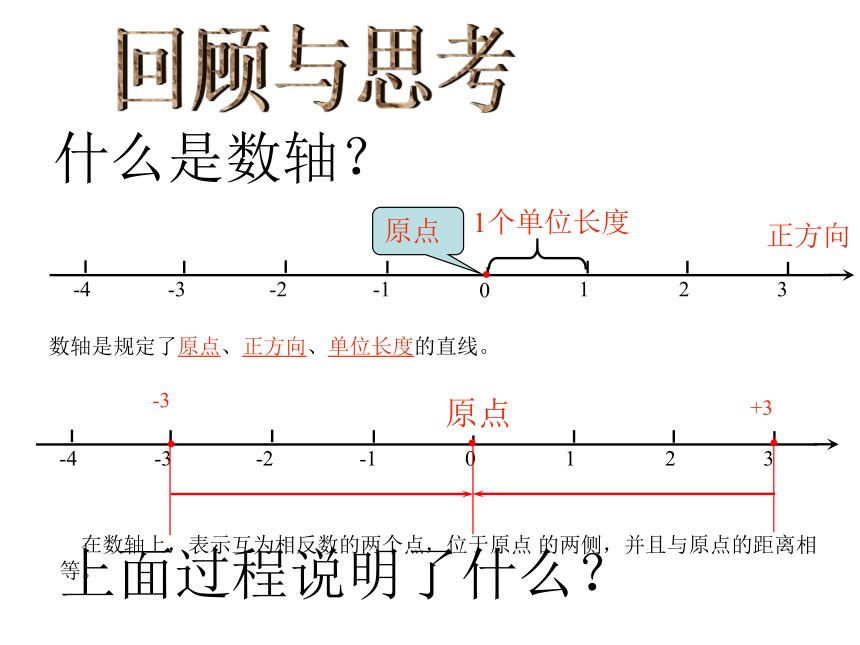
在数轴上，表示互为相反数的两个点，位于原点 的两侧，并且与原点的距离相等。
什么是数轴？
0
-4
-3
-2
-1
3
2
1
1个单位长度
原点
正方向
数轴是规定了原点、正方向、单位长度的直线。
上面过程说明了什么？
0
-4
-3
-2
-1
3
2
1
-3
+3
原点
1.4 绝对值
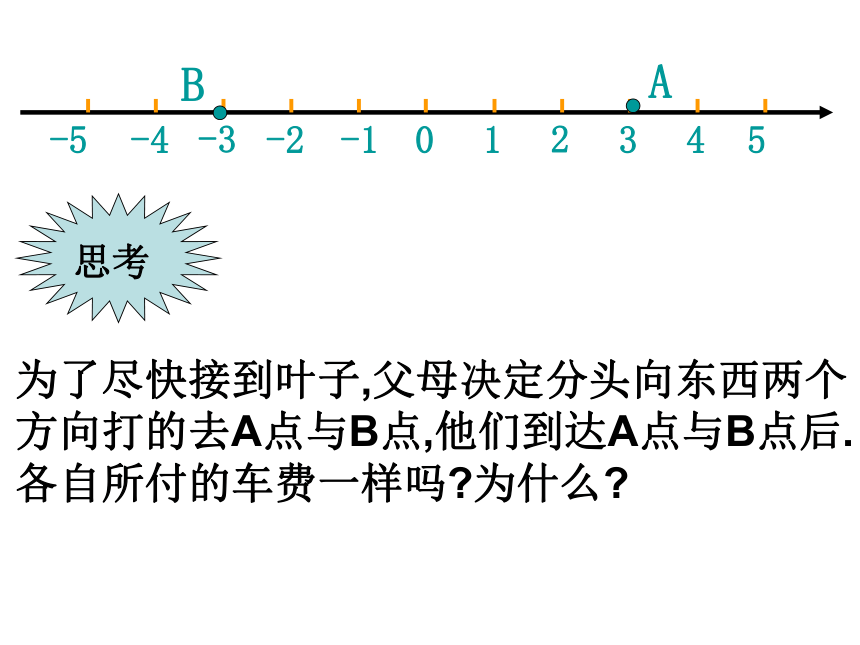
叶子去同学家参加生日聚会
妈妈,我是叶子,
我九点钟回家,你和爸爸
到离我们家3公里的
公路旁接我。
(注:叶子家在公路旁，公路是东西朝向)
叶子父母走出家门正准备打的时
他们犹豫了…
0
1
2
3
4
5
-1
-2
-3
-4
-5
A
B
思考
为了尽快接到叶子,父母决定分头向东西两个
方向打的去A点与B点,他们到达A点与B点后.
各自所付的车费一样吗 为什么
生活中存在无需考虑方向的量。
两小狗距离原点的距离都为3，它的实际意义是什么？
数轴上表示-5和5的点到原点的距离分别
是多少？表示 和 的点呢？
问：
一个数在数轴上对应的点到原点的距离叫做这个数的绝对值。
零到原点的距离是多少？
一个数在数轴上对应的点到原点的距离叫做这个数的绝对值。
例如：数轴上表示-5的点到原点的距离是5，所以-5的
绝对值是5，记做 。5的绝对值也是5，记做
。
零的绝对值为零。
0
1
2
3
4
5
-1
-2
-3
-4
-5
A
B
3
3
数轴上表示+3的点到原点的距离是 __
数轴上表示-3的点到原点的距离是 __
数轴上表示－1.5 的点到原点的距离是 __
数轴上表示 的点到原点的距离是 __
3
3
0
0
＋３的绝对值是３
记做｜＋３｜＝３
－３的绝对值是３
记做｜－３｜＝３
－1.5 的绝对值是
记做
0的绝对值是0
记做｜0｜＝0
1.5
1.5
| －1.5 |= 1.5
例1：求下列各数的绝对值：
解：
一个正数的绝对值是它本身；
一个负数的绝对值是它的相反数；
零的绝对值是零。
互为相反数的两个数的绝对值相等。
一个正数的绝对值是它本身；
一个负数的绝对值是它的相反数；
零的绝对值是零。
互为相反数的两个数的绝对值相等。
任一有理数的绝对值是一个非负数（正数或零）。
做一做：说出下列各数的绝对值：
填表:
相反数 绝对值
21
0
-21
21
0
0
例2:求绝对值等于4的数。（写明理由）
解：
∵数轴上到原点的距离等于4个单位长度的点有两个，即表示+4的点P和-4的点M,
∴绝对值等于4的数是+4和-4.
0
1
2
3
4
5
-1
-2
-3
-4
－5
4
4
P
M
解2： ∵　｜＋４｜＝４　　｜－４｜＝４
　　 ∴绝对值等于4的数是+4和-4.
所以
因为
法1
法2
计算:
判断:
(1)一个数的绝对值一定是正数;
(2)一个数的绝对值不可能是负数；
(3)绝对值是同一个正数的数有两个，它们互为相反数。
错
对
对
练一练
时钟报时的准确程度是衡量时钟质量的一个重要方面,某检测员对A,B,C,D,E五个时钟进行准确性测试,记录了如下数据(记一昼夜后比标准时间早为正,慢为负,单位:秒):
A
B
C
D
E
-10
+3
+5
-1
-7
仅从报时的准确程度来考虑,哪个时钟的质量好一些
1.有理数的绝对值的意义.
代数意义:一个正数的绝对值是 ；
零的绝对值是 ；
一个负数的绝对值是 .
几何意义:表示到原点的距离
小结
2.绝对值的性质：
3.绝对值与相反数的关系：
｜a｜≥０（非负性）
互为相反数的两个数的绝对值 ；
绝对值相等，符号相反的两个数 ；
若|a|=|b|，则
4.绝对值等于本身的数：
5.绝对值为非零数，则原数有
0和正数（非负数）
2个，且互为相反数
它本身
零
它的相反数
相等
互为相反数
a=b或者a=-b